
Função bijetiva o que é, como se faz, exemplos, exercícios

UMA função bijetiva é aquele que atende a dupla condição de ser injetivo e sobrejetivo. Ou seja, todos os elementos do domínio têm uma única imagem no codomínio e, por sua vez, o codomínio é igual à classificação da função ( RF ).
Ele é realizado considerando uma relação um-para-um entre os elementos do domínio e do codomínio. Um exemplo simples é a função F: R → R definido pela linha F (x) = x
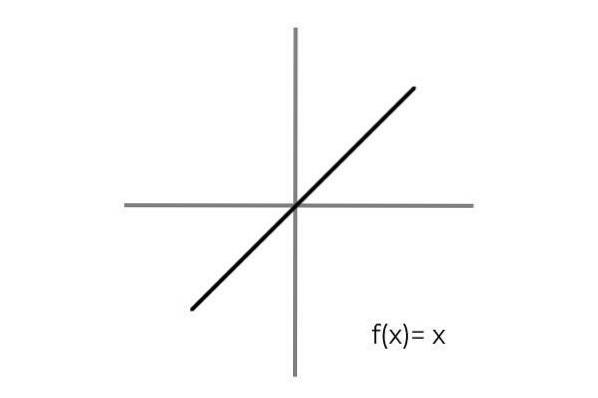
Observa-se que para cada valor do domínio ou conjunto inicial (ambos os termos se aplicam igualmente) existe uma única imagem no codomínio ou conjunto de chegada. Além disso, não há elemento do codomínio que não seja uma imagem.
Desta forma F: R → R definido pela linha F (x) = x é bijetivo
Índice do artigo
- 1 Como você faz uma função bijetiva?
- 1.1 Injetividade de uma função
- 1.2 Surjetividade de uma função
- 1.3 Condicionamento de funções
- 2 Exemplos: exercícios resolvidos
- 2.1 Exercício 1
- 2.2 Exercício 2
- 2.3 Exercício 3
- 2.4 Exercício 4
- 3 exercícios propostos
- 4 referências
Como você faz uma função bijetiva?
Para responder a isso, é necessário ter clareza sobre os conceitos referentes a Injetividade Y Surjetividade de uma função, além dos critérios para funções de condição a fim de adaptá-las aos requisitos.
Injetividade de uma função
Uma função é injetivo quando cada um dos elementos de seu domínio está relacionado a um único elemento do codomínio. Um elemento do codomínio só pode ser a imagem de um único elemento do domínio, desta forma os valores da variável dependente não podem ser repetidos.
Considerar injetivo para uma função, o seguinte deve ser cumprido:
∀ x1 ≠ xdois ⇒ F (x1 ) ≠ F (xdois )
Surjetividade de uma função
Uma função é classificada como sobrejetiva, se cada elemento de seu codomínio é uma imagem de pelo menos um elemento do domínio.
Considerar sobrejetiva para uma função, o seguinte deve ser cumprido:
Ser F: DF → CF
∀ b ℮ CF E para ℮ DF / F (a) = b
Esta é a maneira algébrica de estabelecer que para cada "b" que pertence a CF há um “a” que pertence a DF de modo que, a função avaliada em "a" é igual a "b".
Condicionamento de função
Às vezes, uma função que não é bijetivo, pode estar sujeito a certas condições. Essas novas condições podem torná-lo um função bijetiva. Todos os tipos de modificações no domínio e no codomínio da função são válidos, onde o objetivo é cumprir as propriedades de injetividade e sobrejetividade na relação correspondente..
Exemplos: exercícios resolvidos
Exercício 1
Deixe a função F: R → R definido pela linha F (x) = 5x +1
R: [Todos os números reais]
Observa-se que para cada valor do domínio existe uma imagem no codomínio. Esta imagem é única, o que torna F seja um função injetiva. Da mesma forma, observamos que o codomínio da função é igual ao seu posto. Cumprindo assim a condição de sobrejetividade.
Sendo injetivo e sobrejetivo ao mesmo tempo, podemos concluir que
F: R → R definido pela linha F (x) = 5x +1 é uma função bijetiva.
Isso se aplica a todas as funções lineares (funções cujo maior grau da variável é um).
Exercício 2
Deixe a função F: R → R definido por F (x) = 3xdois - dois
Ao traçar uma linha horizontal, observa-se que o gráfico é encontrado em mais de uma ocasião. Por causa disso, a função F não é injetivo e, portanto, não será bijetivo contanto que seja definido em R → R
Da mesma forma, existem valores do codomínio que não são imagens de nenhum elemento do domínio. Por isso, a função não é sobrejetora, o que também merece condicionar o conjunto de chegada.
Prosseguimos para condicionar o domínio e codomínio da função
F: [0 , ∞] → [ - dois , ∞ ]
Onde se observa que o novo domínio engloba os valores de zero a infinito positivo. Evitando a repetição de valores que afetam a injetividade.
Da mesma forma, o codomínio foi modificado, contando de "-2" ao infinito positivo, eliminando do codomínio os valores que não correspondiam a nenhum elemento do domínio
Desta forma, pode ser garantido que F : [0 , ∞] → [ - dois , ∞ ] definido por F (x) = 3xdois - dois
É bijetivo
Exercício 3
Deixe a função F: R → R definido por F (x) = Sen (x)
No intervalo [ -∞ , +∞ ] a função seno varia seus resultados entre zero e um.
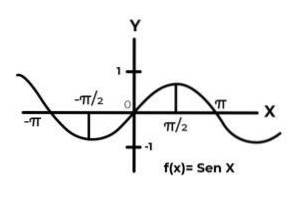
A função F não corresponde aos critérios de injetividade e sobrejetividade, pois os valores da variável dependente se repetem a cada intervalo de π. Também os termos do codomínio fora do intervalo [ -onze ] Eles não são uma imagem de qualquer elemento do domínio.
Ao estudar o gráfico da função F (x) = Sen (x) intervalos são observados onde o comportamento da curva atende aos critérios de bijetividade. Como por exemplo o intervalo DF = [ π / 2,3π / 2 ] para o domínio. Y CF = [-1, 1] para o codomínio.
Onde a função varia resulta de 1 a -1, sem repetir nenhum valor na variável dependente. E ao mesmo tempo o codomínio é igual aos valores adotados pela expressão Sen (x)
Desta forma, a função F: [ π / 2,3π / 2 ] → [-1, 1] definido por F (x) = Sen (x). É bijetivo
Exercício 4
Indique as condições necessárias para DF e CF. Então a expressão
F (x) = -xdois ser bijetivo.
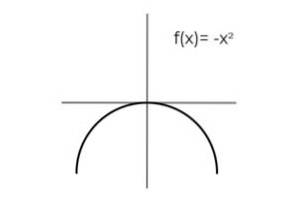
A repetição dos resultados é observada quando a variável assume valores opostos:
F (2) = F (-2) = -4
F (3) = F (-3) = -9
F (4) = F (-4) = -16
O domínio é condicionado, limitando-o ao lado direito da linha real.
DF = [0 , +∞ ]
Da mesma forma, observa-se que o intervalo desta função é o intervalo [ -∞ , 0], que ao atuar como um codomínio cumpre as condições de sobrejetividade.
Desta forma, podemos concluir que
A expressão F: [0 , +∞ ] → [ -∞ , 0] definido por F (x) = -xdois É bijetivo
Exercícios propostos
Verifique se as seguintes funções são bijetivas:
F: [0 , ∞) → R definido por F (x) = 3 (x + 1)dois +dois
F: [ 3π / 2,5π / 2 ] → R definido por F (x) = 5ctg (x)
F: [ -π,π ] → R definido por F (x) = Cos (x - 3)
F: R → R definido pela linha F (x) = -5x + 4
Referências
- Introdução à lógica e ao pensamento crítico. Merrilee H. Salmon. Universidade de Pittsburgh
- Problemas em Análise Matemática. Piotr Biler, Alfred Witkowski. Universidade de Wroclaw. Polônia.
- Elementos de análise abstrata. Mícheál O'Searcoid PhD. Departamento de matemática. Faculdade universitária Dublin, Beldfield, Dublind 4
- Introdução à Lógica e à Metodologia das Ciências Dedutivas. Alfred Tarski, New York Oxford. Imprensa da Universidade de Oxford.
- Princípios de análise matemática. Enrique Linés Escardó. Editorial Reverté S. A 1991. Barcelona Espanha.



Ainda sem comentários