O função constante é aquele em que o valor de y é mantido constante. Em outras palavras: uma função constante sempre tem a forma f (x) = k, Onde k é um número real.
Ao representar graficamente a função constante no sistema de coordenadas xy, sempre resulta em uma linha reta paralela ao eixo horizontal ou eixo do x.
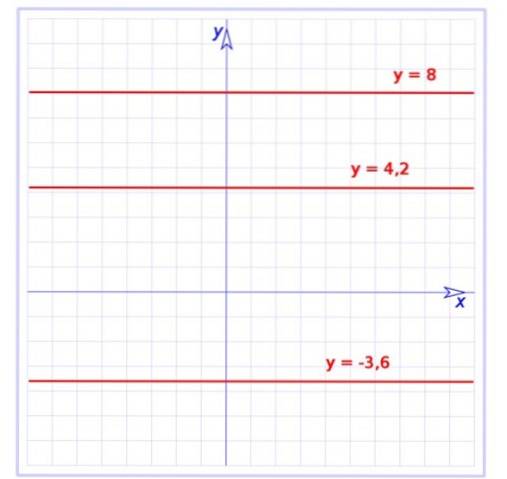
Esta função é um caso particular do função afim, cujo gráfico também é uma linha reta, mas com uma inclinação. A função constante tem inclinação zero, ou seja, é uma linha horizontal, conforme mostrado na figura 1.
Lá, o gráfico de três funções constantes é mostrado:
f (x) = -3,6
g (x) = 4,2
h (x) = 8
Todas são linhas paralelas ao eixo horizontal, a primeira delas está abaixo do referido eixo, enquanto as demais estão acima.
Índice do artigo
Podemos resumir as principais características da função constante da seguinte forma:
-Seu gráfico é uma linha reta horizontal.
-Possui uma única intersecção com o eixo Y, que vale k.
-É contínuo.
-O domínio da função constante (o conjunto de valores que o x) é o conjunto de números reais R.
-O caminho, intervalo ou contra-domínio (o conjunto de valores que a variável assume Y) é simplesmente a constante k.
As funções são necessárias para estabelecer ligações entre as quantidades que dependem umas das outras de alguma forma. A relação entre eles pode ser modelada matematicamente, para descobrir como um deles se comporta quando o outro varia..
Isso ajuda a construir modelos para muitas situações e fazer previsões sobre seu comportamento e evolução..
Apesar de sua aparente simplicidade, a função constante tem muitas aplicações. Por exemplo, quando se trata de estudar magnitudes que permanecem constantes ao longo do tempo, ou pelo menos por um tempo apreciável.
Desta forma, as magnitudes se comportam em situações como as seguintes:
-O velocidade cruzando um carro em uma longa estrada reta. Contanto que você não freie ou acelere, o carro tem um movimento retilíneo uniforme.
-Um capacitor totalmente carregado desconectado de um circuito tem um carregar constante no tempo.
-Finalmente, um estacionamento de taxa fixa mantém um preço constante, não importa quanto tempo um carro fica estacionado lá.
A função constante pode, alternativamente, ser representada da seguinte forma:
f (x) = kx0
Uma vez que qualquer valor de x elevado a 0 dá 1 como resultado, a expressão anterior se reduz à já familiar:
f (x) = k
Claro que isso acontece, desde que o valor de k é diferente de 0.
É por isso que a função constante também é classificada como um função polinomial de grau 0, uma vez que o expoente da variável x é 0.
Responda as seguintes questões:
a) Pode-se afirmar que a reta dada por x = 4 é uma função constante? Motivo da sua resposta.
b) Uma função constante pode ter uma interceptação x?
c) A função f (x) = w constantedois?
Aqui está o gráfico da linha x = 4:
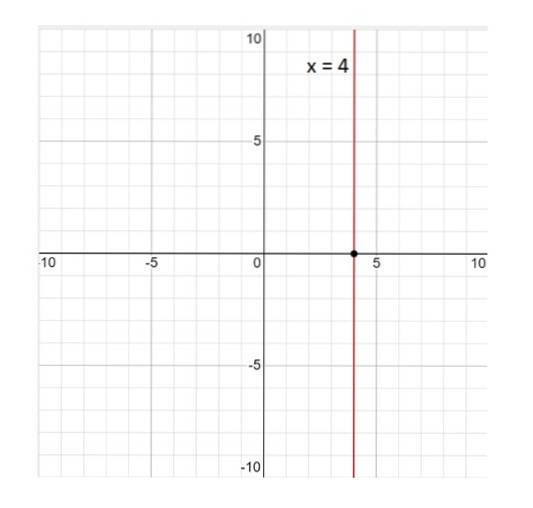
A linha x = 4 não é uma função; por definição, uma função é uma relação tal que a cada valor da variável x corresponde a um único valor de Y. E neste caso isso não é verdade, pois o valor x = 4 está associado a valores infinitos de Y. Portanto, a resposta é não.
Em geral, uma função constante não tem interseção com o eixo x, a menos que seja sobre y = 0, nesse caso, é o eixo x propriamente dito.
Sim desde C é constante, assim como seu quadrado. O que importa é que C não dependa da variável de entrada x.
Encontre a interseção entre as funções f (x) = 5 Y g (x) = 5x - 2
Para encontrar a interseção entre essas duas funções, elas podem ser reescritas respectivamente como:
y = 5; y = 5x - 2
Eles são equalizados, obtendo:
5x - 2 = 5
O que é uma equação linear de primeiro grau, cuja solução é:
5x = 5 + 2 = 7
x = 7/5
O ponto de intersecção é (7 / 5,5).
Mostre que a derivada de uma função constante é 0.
Da definição de derivada, temos:
f (x + h) = k
Substituindo na definição:
Além disso, se pensarmos na derivada como a taxa de mudança dy / dx, a função constante não sofre nenhuma alteração, portanto sua derivada é zero.
Encontre a integral indefinida de f (x) = k.
Uma empresa de telefonia celular oferece serviço de Internet ilimitado por US $ 15 por mês. Qual é a função de preço de acordo com o tempo?
Seja P o preço a pagar em $ e t o tempo, que pode ser expresso em dias. A função é definida assim:
P (t) = 15
O seguinte gráfico de velocidade em função do tempo corresponde ao movimento de uma partícula.
Ele pergunta:
a) Escreva uma expressão para a função de velocidade em função do tempo v (t).
b) Encontre a distância percorrida pelo celular no intervalo de tempo entre 0 e 9 segundos.
No gráfico mostrado, pode-se ver que:
-v = 2 m / s no intervalo de tempo entre 0 e 3 segundos
-O celular fica parado entre 3 e 5 segundos, pois neste intervalo a velocidade é 0.
-v = - 3 m / s entre 5 e 9 segundos.
É um exemplo de função por partes, ou função por partes, que por sua vez é composta por funções constantes, válidas apenas para os intervalos de tempo indicados. Conclui-se que a função procurada é:
A partir do gráfico v (t), pode-se calcular a distância percorrida pelo móvel, que é numericamente equivalente à área sob / na curva. Desta maneira:
-Distância percorrida entre 0 e 3 segundos = 2 m / s. 3 s = 6 m
-Entre 3 e 5 segundos ele ficou parado, portanto não percorreu nenhuma distância.
-Distância percorrida entre 5 e 9 segundos = 3 m / s. 4 s = 12 m
No total, o móvel percorreu 18 m. Observe que embora a velocidade seja negativa no intervalo entre 5 e 9 segundos, a distância percorrida é positiva. O que acontece é que durante esse intervalo de tempo, o celular mudou o sentido de sua velocidade.
Ainda sem comentários