
Função homográfica como representar graficamente, exercícios resolvidos
O funcionouíon homográfico ou racional É um tipo de função matemática composta pela divisão de duas componentes polinomiais. Obedece a forma P (x) / Q (x), onde Q (x) não pode assumir a forma nula.
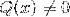
Por exemplo, a expressão (2x - 1) / (x + 3) corresponde a uma função homográfica com P (x) = 2x - 1 e Q (x) = x + 3.

As funções homográficas constituem uma seção de estudo das funções analíticas, sendo tratadas a partir da abordagem gráfica e do estudo do domínio e alcance. Isso se deve às restrições e aos fundamentos que devem ser aplicados para suas deliberações..
Índice do artigo
- 1 O que é uma função homográfica?
- 2 Função homográfica mista
- 2.1 Raiz par enésima da função homográfica
- 2.2 Logaritmo da função homográfica
- 3 Como representar graficamente uma função homográfica?
- 3.1 Raízes
- 3.2 Assíntota vertical
- 3.3 Assíntota horizontal
- 3.4 Intervalo de crescimento
- 3,5 Intervalo de decaimento
- 3.6 Cruzamento com Y
- 4 exemplos
- 4.1 Exercício 1
- 4.2 Exercício 1.2
- 5 Exercício 2
- 6 referências
O que é uma função homográfica?
São expressões racionais de uma única variável, embora isso não signifique que não exista uma expressão semelhante para duas ou mais variáveis, onde já estaria na presença de corpos no espaço que obedecem aos mesmos padrões da função homográfica em o avião.
Têm raízes reais em alguns casos, mas a existência de assíntotas verticais e horizontais é sempre mantida, assim como intervalos de crescimento e decréscimo. Normalmente apenas uma dessas tendências está presente, mas existem expressões capazes de mostrar ambas em seu desenvolvimento..
Seu domínio é restrito pelas raízes do denominador, uma vez que não há divisão por zero dos números reais.
Função homográfica mista
São muito frequentes no cálculo, especialmente diferencial e integral, sendo necessário derivar e antiderivir sob fórmulas particulares. Alguns dos mais comuns são classificados abaixo.
Mesmo enésima raiz da função homográfica
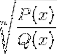
Exclua todos os elementos do domínio que tornam o argumento negativo. As raízes presentes em cada polinômio produzem valores de zero quando avaliados.
Esses valores são aceitos pelo radical, embora a restrição fundamental da função homográfica deva ser considerada. Onde Q (x) não pode receber valores nulos.
As soluções dos intervalos devem ser interceptadas:
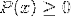
Para se chegar à solução dos cruzamentos, pode-se utilizar o método de sinalização, entre outros.
Logaritmo da função homográfica
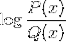
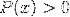
Também é comum encontrar ambas as expressões em uma, entre outras combinações possíveis.
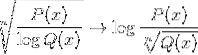
Como representar graficamente uma função homográfica?
As funções homográficas correspondem graficamente às hipérboles no plano. Que são transportados horizontalmente e verticalmente de acordo com os valores que definem os polinômios.
Existem vários elementos que devemos definir para representar graficamente uma função racional ou homográfica.
Estado
O primeiro serão as raízes ou zeros das funções P e Q.
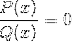
Os valores alcançados serão denotados no eixo x do gráfico. Indicando as interseções do gráfico com o eixo.
Assíntota vertical
Correspondem a linhas verticais, que demarcam o gráfico de acordo com as tendências que apresentam. Eles tocam o eixo x nos valores que fazem o denominador zero e nunca serão tocados pelo gráfico da função homográfica.
Assíntota horizontal
Representado por uma linha de costura horizontal, demarca um limite para o qual a função não será definida no ponto exato. As tendências serão observadas antes e depois desta linha.
Para calculá-lo devemos recorrer a um método semelhante ao método de L'Hopital, usado para resolver limites de funções racionais que tendem ao infinito. Devemos pegar os coeficientes das maiores potências no numerador e denominador da função.
Por exemplo, a seguinte expressão tem uma assíntota horizontal em y = 2/1 = 2.
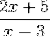
Intervalo de crescimento
Os valores das ordenadas terão tendências marcadas no gráfico devido às assíntotas. No caso de crescimento, a função aumentará em valores conforme os elementos do domínio são avaliados da esquerda para a direita.
Diminuir intervalo
Os valores das ordenadas irão diminuir à medida que os elementos do domínio são avaliados da esquerda para a direita.
Os saltos encontrados nos valores não serão considerados na medida em que aumentem ou diminuam. Isso ocorre quando o gráfico está próximo de uma assíntota vertical ou horizontal, onde os valores podem variar de infinito a infinito negativo e vice-versa..
Intersecção Y
Definindo o valor de x como zero, encontramos a interceptação com o eixo das ordenadas. Esta é uma informação muito útil para obter o gráfico da função racional.
Exemplos
Defina o gráfico das seguintes expressões, encontre suas raízes, assíntotas verticais e horizontais, intervalos de crescimento e decréscimo e interseção com o eixo das ordenadas.
Exercício 1
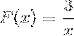
A expressão não tem raízes, pois possui um valor constante no numerador. A restrição a aplicar será x diferente de zero. Com assíntota horizontal em y = 0 e assíntota vertical em x = 0. Não há pontos de intersecção com o eixo y.
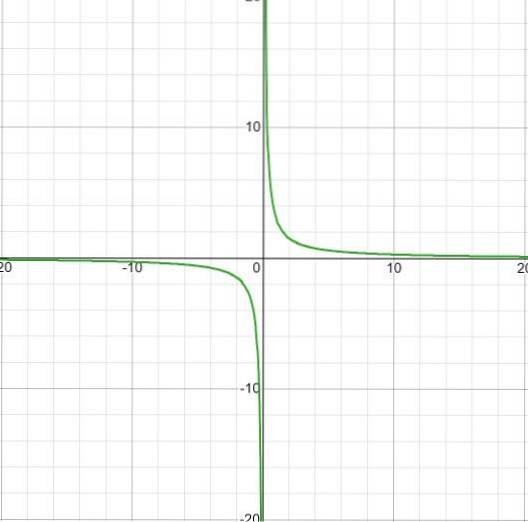
Observa-se que não há intervalos de crescimento mesmo com o salto de menos para mais infinito em x = 0.
O intervalo de decaimento é
ID: (-∞; o) U (0, ∞)
Exercício 1.2
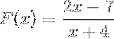
2 polinômios são observados como na definição inicial, então procedemos de acordo com os passos estabelecidos.
A raiz encontrada é x = 7/2, que resulta da definição da função igual a zero.
A assíntota vertical está em x = - 4, que é o valor excluído do domínio pela condição de função racional.
A assíntota horizontal está em y = 2, isto depois de dividir 2/1, os coeficientes das variáveis de grau 1.
Tem uma interceptação y = - 7/4. Valor encontrado após igualar x a zero.
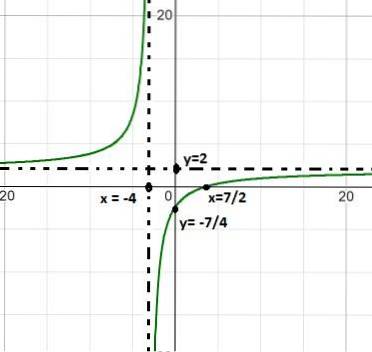
A função cresce constantemente, com um salto de mais para menos infinito em torno da raiz x = -4.
Seu intervalo de crescimento é (-∞, - 4) U (- 4, ∞).
Quando o valor de x se aproxima de menos infinito, a função assume valores próximos a 2. O mesmo acontece quando x se aproxima de mais infinito.
A expressão se aproxima de mais infinito ao avaliar a - 4 da esquerda, e de menos infinito ao avaliar a - 4 da direita.
Exercício 2
O gráfico da seguinte função homográfica é observado:
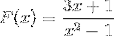
Descreva seu comportamento, raízes, assíntotas verticais e horizontais, intervalos de crescimento e decréscimo e intersecção com o eixo das ordenadas..
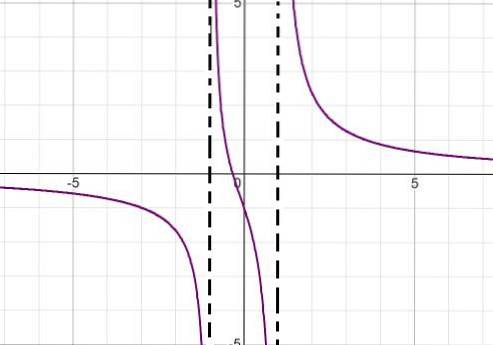
O denominador da expressão nos informa, fatorando a diferença dos quadrados (x + 1) (x - 1), os valores das raízes. Desta forma, ambas as assíntotas verticais podem ser definidas como:
x = -1 e x = 1
A assíntota horizontal corresponde ao eixo das abscissas porque a maior potência está no denominador.
Sua única raiz é definida por x = -1/3.
A expressão sempre diminui da esquerda para a direita. Ele se aproxima de zero ao se aproximar do infinito. Menos infinito conforme você se aproxima de -1 da esquerda. Um mais infinito à medida que se aproxima de -1 da direita. Menos infinito ao se aproximar de 1 da esquerda e mais infinito ao se aproximar de 1 da direita.
Referências
- Aproximação com funções racionais. Donald J. Newman. American Mathematical Soc., 31 de dezembro. 1979
- Funções racionais ortogonais. UNIVERSIDAD DE LA LAGUNA TENERIFE ADHEMAR BULTHEEL, Adhemar Bultheel, Pablo Gonzalez-Vera, Erik Hendriksen, Olav Njastad. Cambridge University Press, 13 de fevereiro. 1999
- Aproximação racional de funções reais. P. P. Petrushev, Vasil Atanasov Popov. Cambridge University Press, 3 de março. 2011
- Funções algébricas. Gilbert Ames Bliss. Courier Corporation, 1º de janeiro 2004
- Journal of the Spanish Mathematical Society, Volumes 5-6. Sociedade Espanhola de Matemática, Madrid 1916



Ainda sem comentários