
Propriedades da função logarítmica, exemplos, exercícios
O função logarítmica é uma relação matemática que associa cada número real positivo x com seu logaritmo Y em uma base para. Essa relação atende aos requisitos para ser uma função: cada elemento x pertencente ao domínio possui uma imagem única.
Portanto:
f (x) = y = logpara x , com a> 0 e diferente de 1.
As principais propriedades da função logarítmica são:
-Seu domínio é todo real maior que 0, não incluindo 0. Em outras palavras, não há logaritmo de 0 ou números negativos em nenhuma base. Na forma de intervalo:
sol F = (0, ∞ +)
-O logaritmo de um número pode ser negativo, positivo ou 0, então seu intervalo ou intervalo é:
Rgo F = (-∞, ∞ +)
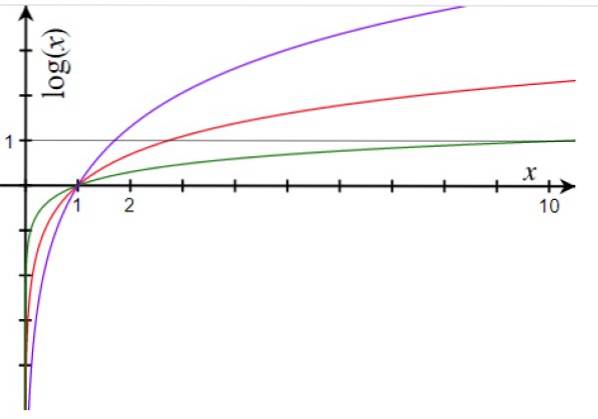
-A função logarítmica está sempre aumentando para a> 1 e diminuindo para uma<1.
-O inverso de f (x) = logpara x é a função exponencial.
Na verdade, a função logarítmica baseada em, é a função inversa da função potencial:
F-1(x) = aY
Já que o logaritmo na base para de um número x, É o numero Y para o qual a base deve ser elevada para para obter x.
-O logaritmo da base é sempre 1. Assim, o gráfico de f (x) = logpara x sempre cruza o eixo x no ponto (1,0)
-A função logarítmica é transcendente e não pode ser expresso como um polinômio ou como um quociente destes. Além do logaritmo, este grupo inclui as funções trigonométricas e exponenciais, entre outras.
Índice do artigo
- 1 exemplos
- 2 As vantagens dos logaritmos
- 2.1 Exemplo
- 3 Exercício de aplicação: a escala Richter
- 3.1 Solução
- 4 referências
Exemplos
A função logarítmica pode ser estabelecida por várias bases, mas as mais utilizadas são 10 e e, Onde e é o número de Euler igual a 2,71828 ... .
Quando a base 10 é usada, o logaritmo é chamado de logaritmo decimal, logaritmo vulgar, Briggs ou simplesmente logaritmo simples.
E se o número e for usado, ele será chamado de logaritmo natural, por John Napier, o matemático escocês que descobriu os logaritmos..
A notação usada para cada um é a seguinte:
-Logaritmo decimal: log10 x = log x
-Logaritmo natural: ln x
Quando se pretende utilizar outra base, é absolutamente necessário indicá-la como subscrito, pois o logaritmo de cada número é diferente dependendo da base a utilizar. Por exemplo, se forem logaritmos na base 2, escreva:
y = logdois x
Vejamos o logaritmo do número 10 em três bases diferentes, para ilustrar este ponto:
log 10 = 1
ln 10 = 2,30259
registrodois 10 = 3,32193
Calculadoras comuns trazem apenas logaritmos decimais (função log) e logaritmo natural (função ln). Na Internet existem calculadoras com outras bases. Em qualquer caso, o leitor pode verificar, com a sua ajuda, que os valores acima são verdadeiros:
101 = 10
e2,3026 = 10.0001
dois3,32193 = 10,0000
Pequenas diferenças decimais são devidas ao número de casas decimais tomadas no cálculo do logaritmo.
As vantagens dos logaritmos
Entre as vantagens de usar logaritmos está a facilidade que eles fornecem para trabalhar com grandes números, usando seu logaritmo em vez do número diretamente.
Isso é possível porque a função logaritmo cresce mais lentamente conforme os números aumentam, como podemos ver no gráfico.
Portanto, mesmo com números muito grandes, seus logaritmos são muito menores e manipular pequenos números é sempre mais fácil..
Além disso, os logaritmos têm as seguintes propriedades:
-produtos: log (a.b) = log a + log b
-Quociente: log (a / b) = log a - log b
-Poder: log ab = b.log a
E, dessa forma, os produtos e quocientes tornam-se adições e subtrações de números menores, enquanto a potenciação torna-se um produto simples, embora a potência seja alta..
É por isso que os logaritmos nos permitem expressar números que variam em faixas muito grandes de valores, como a intensidade do som, o pH de uma solução, o brilho das estrelas, a resistência elétrica e a intensidade dos terremotos na escala Richter..

Vejamos um exemplo do tratamento das propriedades dos logaritmos:
Exemplo
Encontre o valor de x na seguinte expressão:
log (5x +1) = 1 + log (2x-1)
Responder
Temos aqui uma equação logarítmica, já que a incógnita está no argumento do logaritmo. Ele é resolvido deixando um único logaritmo em cada lado da igualdade.
Começamos colocando todos os termos que contêm "x" à esquerda da igualdade e aqueles que contêm apenas números à direita:
log (5x + 1) - log (2x-1) = 1
À esquerda temos a subtração de dois logaritmos, que podem ser escritos como o logaritmo de um quociente:
log [(5x + 1) / (2x-1)] = 1
Porém, à direita está o número 1, que podemos expressar como log 10, como vimos anteriormente. Então:
log [(5x + 1) / (2x-1)] = log 10
Para que a igualdade seja cumprida, argumentos dos logaritmos devem ser iguais:
(5x + 1) / (2x-1) = 10
5x + 1 = 10 (2x - 1)
5x + 1 = 20 x - 10
-15 x = -11
x = 15/11
Exercício de aplicação: a escala Richter
Em 1957, um terremoto ocorreu no México, cuja magnitude foi de 7,7 na escala Richter. Em 1960 outro terremoto de maior magnitude ocorreu no Chile, de 9,5.
Calcule quantas vezes o terremoto no Chile foi mais intenso que o do México, sabendo que a magnitude MR na escala Richter é dada pela fórmula:
MR = log (104 EU)
Solução
A magnitude de um terremoto na escala Richter é uma função logarítmica. Vamos calcular a intensidade de cada terremoto, já que temos as magnitudes Richter. Vamos fazer isso passo a passo:
-México: 7,7 = log (104 EU)
Como o inverso da função logaritmo é o exponencial, aplicamos isso a ambos os lados da igualdade com a intenção de resolver para I, que se encontra no argumento do logaritmo.
Como são logaritmos decimais, a base é 10. Então:

10 7,7 = 104 eu
A intensidade do terremoto no México foi:
euM = 10 7,7 / 104 = 103,7
-Pimenta: 9,5 = log (104 EU)
O mesmo procedimento nos leva à intensidade do terremoto chileno ICH:
euCH = 10 9,5 / 104 = 105,5
Agora podemos comparar as duas intensidades:
euCH / EUM = 105,5 / 103,7 = 101,8 = 63,1
euCH = 63,1. euM
O terremoto no Chile foi cerca de 63 vezes mais intenso do que no México. Como a magnitude é logarítmica, ela cresce mais lentamente do que a intensidade, então uma diferença de 1 na magnitude significa uma amplitude 10 vezes maior da onda sísmica.
A diferença entre as magnitudes de ambos os terremotos é de 1,8, portanto poderíamos esperar uma diferença de intensidades mais próxima de 100 do que de 10, como realmente aconteceu..
Na verdade, se a diferença fosse exatamente 2, o terremoto chileno teria sido 100 vezes mais intenso que o mexicano..
Referências
- Carena, M. 2019. Manual de Matemática Pré-Universitária. Universidade Nacional do Litoral.
- Figuera, J. 2000. Mathematics 1st. Ano diversificado. Edições CO-BO.
- Jiménez, R. 2008. Algebra. Prentice Hall.
- Larson, R. 2010. Cálculo de uma variável. 9º. Edição. Colina Mcgraw.
- Stewart, J. 2006. Pré-cálculo: Matemática para Cálculo. 5 ª. Edição. Cengage Learning.


Ainda sem comentários