
Funções trigonométricas básicas, no plano cartesiano, exemplos, exercícios
As funções trigonométricas da variável real correspondem a qualquer ângulo (expresso em radianos), uma razão trigonométrica, que pode ser seno, cosseno, tangente, cotangente, secante e cossecante.
Desta forma, temos as seis funções trigonométricas: seno, cosseno, tangente, cossecante, secante e cotangente..
As funções trigonométricas para ângulos entre 0 e 2π são definidas com o auxílio do círculo unitário, de raio 1 e cujo centro coincide com o da origem do sistema de coordenadas cartesianas: o ponto (0,0).
Podemos localizar qualquer ponto P de coordenadas (x, y) nesta circunferência.
O segmento que une a origem com P, junto com os respectivos segmentos que unem as projeções de P nos eixos das coordenadas, formam um triângulo retângulo, cujas relações trigonométricas são conhecidas como relações entre os lados do triângulo. A) Sim:
- sen θ = perna oposta / hipotenusa
- cos θ = perna adjacente / hipotenusa
- tg θ = perna oposta / perna adjacente
E agora os motivos que são inversos aos anteriores:
- sec θ = hipotenusa / perna adjacente
- cosec θ = hipotenusa / perna oposta
- ctg θ = perna adjacente / perna oposta
No círculo unitário, a hipotenusa de qualquer triângulo é igual a 1 e as pernas valem x e y, então:
sin θ = y
cos θ = x
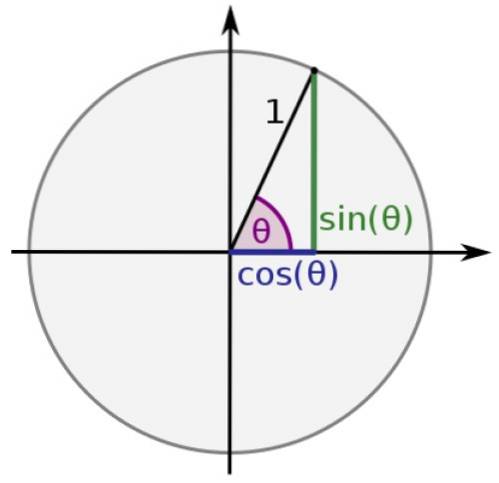
Desta forma, as funções seno e cosseno sempre adquirem valores entre -1 e 1, enquanto o resto:
tg θ = y / x
cosec θ = 1 / y
seg θ = 1 / x
Eles não são definidos quando x ou Y vale 0.
Índice do artigo
- 1 Funções trigonométricas no plano cartesiano
- 1.1 Função f (x) = sin x
- 1.2 Função f (x) = cos x
- 1.3 Funções trigonométricas descontínuas
- 2 Exercício resolvido
- 2.1 Solução
- 3 referências
Funções trigonométricas no plano cartesiano
Como veremos a seguir, as funções trigonométricas são caracterizadas por serem periódicas. Portanto, eles não são bijetivos, exceto em um domínio restrito..
Função f (x) = sin x
Começando no círculo trigonométrico no ponto P (1,0), o ângulo é de 0 radianos. Em seguida, o raio gira no sentido anti-horário e a função sen x cresce gradualmente até atingir π / 2 radianos (90º), equivalente a aproximadamente 1.571 radianos..
Lá ele atinge o valor y = 1 e então diminui até chegar a zero em π radianos (180 °). Mais tarde diminui ainda mais, pois o valor torna-se negativo até atingir -1 quando o ângulo é 3π / 2 radianos (270 °).
Por fim, aumenta novamente até voltar a zero em 360 °, onde tudo começa novamente. Isso faz com que y = sin x a função periódica do período 2π, portanto, a função seno não é bijetiva.
Além disso, o gráfico é simétrico em relação ao ponto (0,0), portanto, a função é ímpar.
Então o gráfico de y = sin x:
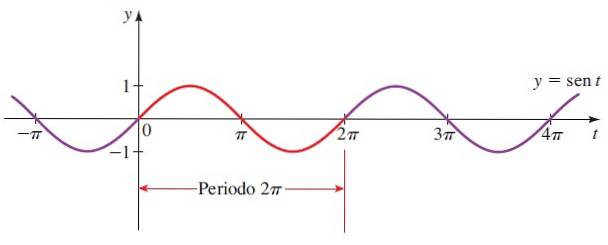
A seção em vermelho é o primeiro período. Os ângulos negativos também são considerados, uma vez que o raio do círculo trigonométrico pode girar no sentido horário.
Domínio de sin x = Todos em reais.
Alcance ou caminho de sen x = [-1,1]
Função f (x) = cos x
No ponto P (1,0) a função cosseno vale 1 e a partir daí diminui, chegando a 0 quando o ângulo é π / 2. Ele continua diminuindo e assume valores negativos, até atingir -1 no ângulo π.
Em seguida, começa a aumentar gradualmente até atingir 0 em 3π / 2 e retorna ao valor 1 quando o raio deu uma volta completa. A partir daí o ciclo se repete, uma vez que cos x é periódico e também é par (simétrico em torno do eixo vertical).
A forma da função cosseno é a mesma da função seno, exceto que eles são deslocados π / 2 um em relação ao outro..
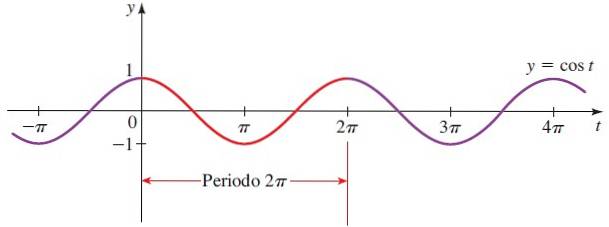
Domínio do cos x = Todos em reais.
Alcance de custo x ou viagem = [-1,1]
Funções trigonométricas descontínuas
As funções tg x, ctg x, sec x e cosec x são descontínuas, pois são quocientes entre seno e cosseno, ou o inverso. Como estes valem 0 em alguns ângulos, quando aparecem no denominador tornam a função descontínua.
E como seno e cosseno são funções periódicas, as funções tg x, ctg x, sec x, cosec x também são periódicas..
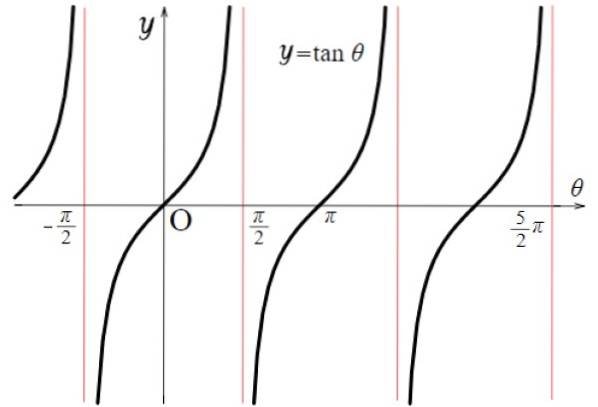
Função tangente f (x) = tg x
Para a função tangente, os valores de descontinuidade são: ± π / 2, ± 3π / 2, ± 5π / 2… Nesse caso, a função assume valores muito grandes ou muito pequenos. Em geral, isso acontece para todos os múltiplos de π da forma (2n + 1) π / 2, tanto positivos quanto negativos, com n = 0, 1, 2 ...
Portanto:
Domínio Tg x: D = x ∈ R / x ≠ (2n + 1) π / 2; n ∈ Z
Alcance ou viagem Tg x: Tudo real.
Observe que a função f (x) = tg x se repete entre - π / 2 e + π / 2, portanto seu período é π. Além disso, é simétrico em relação à origem.
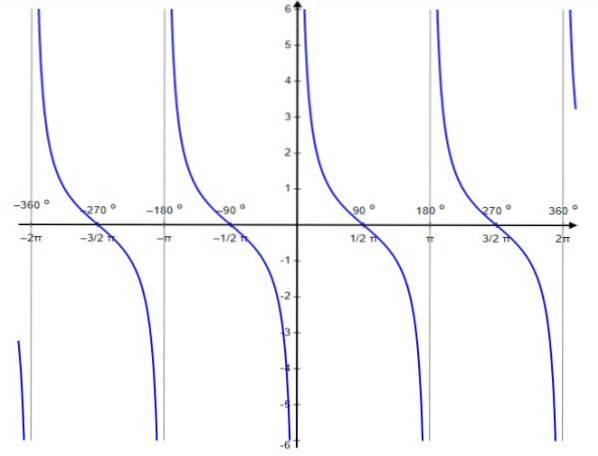
Função cotangente f (x) = ctg x
Para esta função, os valores de descontinuidade ocorrem em 0, ± π, ± 2π ..., ou seja, os múltiplos inteiros de π.
Como a função tangente, a função cotangente é periódica do período π. Para ela é verdade que:
Domínio Ctg x: D = x ∈ R / x ≠ n π; n ∈ Z
Ctg x alcance ou viagem: Tudo real.
Função secante f (x) = sec x
A função sec x tem pontos de descontinuidade em ± π / 2, ± 3π / 2, ± 5π / 2 ..., onde cos x = 0. Também é periódica com período π e também é observado no gráfico que a função nunca leva valores no intervalo (-1,1)
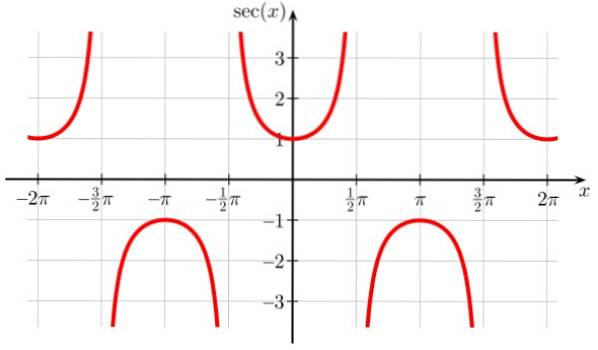
Domínio do s. X: D = x ∈ R / x ≠ (2n + 1) π / 2; n ∈ Z
Alcance ou viagem Sec x: Todos em reais, exceto (-1,1)
Função cossecante f (x) = cossec x
É semelhante à função secante, embora seja deslocada para a direita, portanto os pontos de descontinuidade são 0, ± π, ± 2π e todos os múltiplos inteiros de π. Também é periódico.
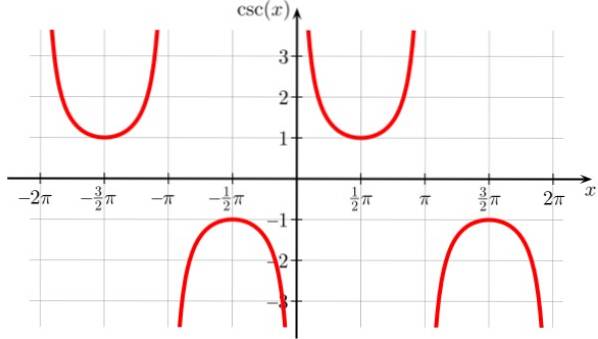
Cosec Domain X: D = x ∈ R / x ≠ n π; n ∈ Z
Faixa de colheita ou caminho x: Todos em reais exceto (-1,1)
Exercício resolvido
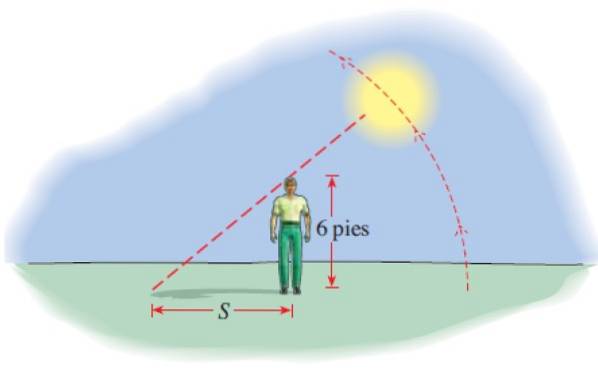
Um homem de 6 pés de altura projeta uma sombra S cujo comprimento é dado por:
S (t) = 6 │cot (π.t / 12) │
Com S em pés e t o número de horas desde as 6h. Qual é a altura da sombra às 8h, 12h, 14h e 17h45?
Solução
Devemos avaliar a função para cada um dos valores dados, note que deve assumir o valor absoluto, já que o comprimento da sombra é positivo:
-Às 8h, 2 horas se passaram das 6h, portanto, t = 2 e S (t) é:
S (2) = 6 │cot (π.2 / 12) │ft = 6 │cot (π / 6) │ft = 10,39 pés.
-Quando é 12 N, t = 6 horas se passaram, portanto:
S (6) = 6 │cot (π.6 / 12) │ft = 6 │cot (π / 2) │ft = 0 pés. (Nesse momento, o Sol cai verticalmente na cabeça da pessoa).
-Às 14h t = 8 horas se passaram:
S (8) = 6 │cot (π.8 / 12) │ft = 6 │cot (2π / 3) │ft = 3,46 pés.
-Quando são 17h45, já se passaram 11,75 horas desde as 6h, então:
S (11,75) = 6 │cot (π x 11,75 / 12) │pés = 91,54 pés. A esta hora as sombras estão ficando mais longas.
O leitor pode calcular o tempo em que a sombra da pessoa se iguala à sua altura??
Referências
- Carena, M. 2019. Manual de Matemática Pré-Universitária. Universidade Nacional do Litoral.
- Figuera, J. 1999. Mathematics. 1ª Diversificado. Bolivarian Collegiate Editions.
- Hoffman, J. Selection of Mathematics Topics. Volume 4.
- Jiménez, R. 2008. Algebra. Prentice Hall.
- Zill, D. 1984. Algebra and Trigonometry. Colina Mcgraw.


Ainda sem comentários