O geometria euclidiana corresponde ao estudo das propriedades dos espaços geométricos onde os axiomas de Euclides são satisfeitos. Embora esse termo às vezes seja usado para abranger geometrias que têm dimensões mais altas com propriedades semelhantes, geralmente é sinônimo de geometria clássica ou geometria plana..
No século III a. C. Euclides e seus discípulos escreveram o Elementos, uma obra que abarcou o conhecimento matemático da época dotado de uma estrutura lógico-dedutiva. Desde então a geometria se tornou uma ciência, inicialmente para resolver problemas clássicos e evoluiu para uma ciência formativa que ajuda a raciocinar..
Índice do artigo
Para falar da história da geometria euclidiana, é fundamental começar por Euclides de Alexandria e a Elementos.
Quando o Egito foi deixado nas mãos de Ptolomeu I, após a morte de Alexandre, o Grande, ele iniciou seu projeto em uma escola em Alexandria.
Entre os sábios que ensinavam na escola estava Euclides. Especula-se que seu nascimento data de aproximadamente 325 AC. C. e sua morte de 265 a. C. Podemos saber com certeza que ele foi para a escola de Platão.
Por mais de trinta anos, Euclides ensinou em Alexandria, construindo seus famosos elementos: ele começou a escrever uma descrição exaustiva da matemática de seu tempo. Os ensinamentos de Euclides produziram discípulos excelentes, como Arquimedes e Apolônio de Perga.
Euclides foi encarregado de estruturar as descobertas díspares dos antigos gregos no Elementos, mas, ao contrário de seus predecessores, não se limita a afirmar que um teorema é verdadeiro; Euclides oferece uma demonstração.
O Elementos eles são um compêndio de treze livros. Depois da Bíblia, é o livro mais publicado, com mais de mil edições.
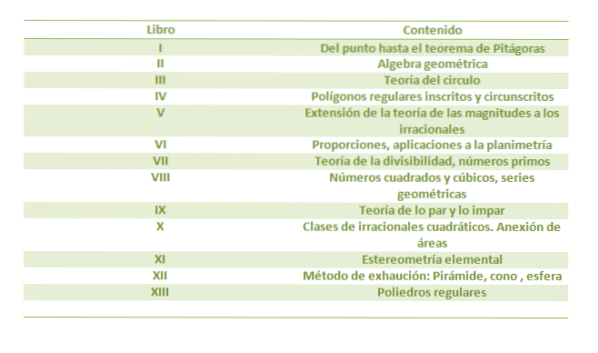
O Elementos é a obra-prima de Euclides no campo da geometria, e oferece um tratamento definitivo da geometria de duas dimensões (o plano) e três dimensões (espaço), sendo esta a origem do que hoje conhecemos como geometria euclidiana..
Os elementos são compostos por definições, noções comuns e postulados (ou axiomas) seguidos de teoremas, construções e provas..
- Um ponto é aquele que não tem partes.
- Uma linha é um comprimento que não tem largura.
- Uma linha reta é aquela que se encontra igualmente em relação aos pontos que estão neste.
- Se duas linhas são cortadas de modo que os ângulos adjacentes sejam iguais, os ângulos são chamados de ângulos retos e as linhas são chamadas de perpendiculares.
- Linhas paralelas são aquelas que, estando no mesmo plano, nunca se cruzam.
Após essas e outras definições, Euclides nos apresenta uma lista de cinco postulados e cinco noções..
- Duas coisas que são iguais a um terço são iguais uma à outra.
- Se as mesmas coisas forem adicionadas às mesmas coisas, os resultados serão os mesmos.
- Se coisas iguais são subtraídas de coisas iguais, os resultados são iguais.
- Coisas que combinam são iguais entre si.
- O total é maior do que uma parte.
- Uma e apenas uma linha passa por dois pontos diferentes.
- As linhas retas podem ser estendidas indefinidamente.
- Um círculo pode ser desenhado com qualquer centro e qualquer raio.
- Todos os ângulos retos são iguais.
- Se uma linha reta cruza duas linhas retas de modo que os ângulos internos do mesmo lado somam menos de dois ângulos retos, então as duas linhas se cruzarão naquele lado..
Este último postulado é conhecido como postulado paralelo e foi reformulado da seguinte forma: "Para um ponto fora de uma linha, um único paralelo à linha dada pode ser traçado".
Aqui estão alguns teoremas do Elementos servirão para mostrar propriedades de espaços geométricos onde se cumprem os cinco postulados de Euclides; Além disso, eles ilustrarão o raciocínio lógico-dedutivo que este matemático usou.
Se dois triângulos têm dois lados e o ângulo entre eles é igual, os outros lados e os outros ângulos são iguais..
Sejam ABC e A'B'C 'dois triângulos com AB = A'B', AC = A'C 'e os ângulos BAC e B'A'C' iguais. Vamos mover o triângulo A'B'C 'de modo que A'B' coincida com AB e que o ângulo B'A'C 'coincida com o ângulo BAC.
Assim, a linha A'C 'coincide com a linha AC, de modo que C' coincide com C. Então, pelo postulado 1, a linha BC deve coincidir com a linha B'C '. Portanto os dois triângulos coincidem e, conseqüentemente, seus ângulos e seus lados são iguais.
Se um triângulo tiver dois lados iguais, os ângulos opostos desses lados são iguais..
Suponha que o triângulo ABC tenha lados iguais AB e AC.
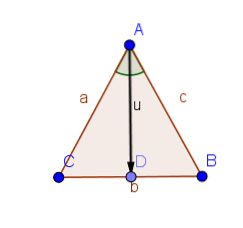
Portanto, os triângulos ABD e ACD têm dois lados iguais e os ângulos entre eles são iguais. Assim, pela Proposição 1.4, os ângulos ABD e ACD são iguais.
Você pode construir uma linha paralela a uma linha dada por um determinado ponto.
Dada uma linha L e um ponto P, uma linha M é desenhada através de P e intercepta L. Em seguida, uma linha N é desenhada através de P que intercepta L. Agora, uma linha N é desenhada através de P que intercepta M, formando um ângulo igual a aquele que L forma com M.
N é paralelo a L.
Suponha que L e N não sejam paralelos e se cruzem em um ponto A. Seja B um ponto em L além de A. Considere a linha O que passa por B e P. Então, O cruza M em ângulos que somam menos de dois em linha reta.
Então, por 1,5 a linha O deve cruzar a linha L no outro lado de M, então L e O se cruzam em dois pontos, o que contradiz o Postulado 1. Portanto, L e N devem ser paralelos.
Ainda sem comentários