O heptadecágono é um polígono regular com 17 lados e 17 vértices. Sua construção pode ser feita no estilo euclidiano, ou seja, utilizando apenas régua e compasso. Foi o grande gênio matemático Carl Friedrich Gauss (1777-1855), com apenas 18 anos, que encontrou o procedimento para sua construção em 1796.
Ao que parece, Gauss sempre foi muito inclinado a esta figura geométrica, a tal ponto que desde o dia em que descobriu a sua construção decidiu ser matemático. Também é dito que ele queria que o heptadecágono fosse gravado em sua lápide.
Gauss também encontrou a fórmula para determinar quais polígonos regulares têm a possibilidade de serem construídos com régua e compasso, já que alguns não possuem construção euclidiana exata..
Índice do artigo
Quanto às suas características, como qualquer polígono, a soma de seus ângulos internos é importante. Em um polígono regular de n lados, a soma é dada por:
Sa (n) = (n -2) * 180º.
Para o heptadecágono, o número de lados n isso é 17, o que significa que a soma de seus ângulos internos é:
Sa (17) = (17 - 2) * 180º = 15 * 180º = 2700º.
Essa soma, expressa em radianos, é assim:
Sa (17) = (17 - 2) * π = 15 * π = 15π
A partir das fórmulas acima, pode ser facilmente deduzido que cada ângulo interno de um heptadecágono tem uma medida exata α dada por:
α = 2700º / 17 = (15/17) π radianos
Conclui-se que o ângulo interno na forma aproximada é:
α ≈ 158.824º
Diagonais e perímetro são outros aspectos importantes. Em qualquer polígono, o número de diagonais é:
D = n (n - 3) / 2 e no caso do heptadecágono, como n = 17, é então que D = 119 diagonais.
Por outro lado, se o comprimento de cada lado do heptadecágono for conhecido, então o perímetro do heptadecágono regular é encontrado simplesmente adicionando 17 vezes esse comprimento, ou o que é equivalente a 17 vezes o comprimento d Em cada lado:
P = 17 d
Às vezes, apenas o raio é conhecido r do heptadecágono, por isso é necessário desenvolver uma fórmula para este caso.
Para tanto, o conceito de apótema. O apótema é o segmento que vai do centro do polígono regular ao ponto médio de um lado. O apótema em relação a um lado é perpendicular a esse lado (ver figura 2).
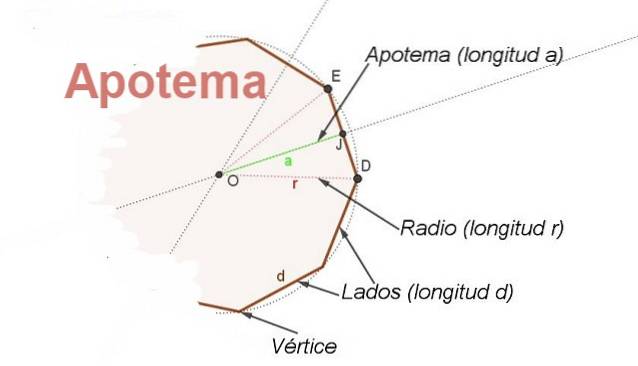
Além disso, o apótema é a bissetriz do ângulo com o vértice central e os lados em dois vértices consecutivos do polígono, o que permite encontrar uma relação entre o raio r e o lado d.
Se é chamado β para o ângulo central CORÇA e levando em consideração que o apotema OJ é a bissetriz que você tem EJ = d / 2 = r Sen (β / 2), de onde há uma relação para encontrar o comprimento d do lado de um polígono conhecido seu raio r e seu ângulo central β:
d = 2 r Sen (β / 2)
No caso do heptadecágono β = 360º / 17 Então você tem:
d = 2 r Sen (180º / 17) ≈ 0,3675 r
Por fim, obtém-se a fórmula para o perímetro do heptadecágono, conhecido seu raio:
P = 34 r Sen (180º / 17) ≈ 6,2475 r
O perímetro de um heptadecágono é próximo ao perímetro da circunferência que o circunda, mas seu valor é menor, ou seja, o perímetro do círculo circunscrito é Pcir = 2π r ≈ 6,2832 r.
Para determinar a área do heptadecágono, nos referiremos à figura 2, que mostra os lados e o apótema de um polígono regular de n lados. Nesta figura o triângulo EOD tem uma área igual à base d (lado do polígono) vezes a altura para (apótema poligonal) dividido por dois:
Área EOD = (d x a) / 2
Tão conhecido o apótema para do heptadecágono e do lado d sua área é:
Área do heptadecágono = (17/2) (d x a)
Para obter uma fórmula para a área do heptadecágono conhecendo o comprimento de seus dezessete lados, é necessário obter uma relação entre o comprimento do apótema. para e o lado d.
Com referência à figura 2, a seguinte relação trigonométrica é obtida:
Castanho (β / 2) = EJ / OJ = (d / 2) / a, sendo β para o ângulo central CORÇA. Então, o apótema para pode ser calculado se o comprimento for conhecido d do lado do polígono e do ângulo central β:
a = (d / 2) Cotan (β / 2)
Se esta expressão for substituída pelo apótema, na fórmula para a área do heptadecágono obtida na seção anterior, temos:
Área do heptadecágono = (17/4) (ddois) Cotan (β / 2)
Sendo β = 360º / 17 para o heptadecágono, então finalmente temos a fórmula desejada:
Área do heptadecágono = (17/4) (ddois) Cotan (180º / 17)
Nas seções anteriores, uma relação foi encontrada entre o lado d de um polígono regular e seu raio r, sendo esta relação a seguinte:
d = 2 r Sen (β / 2)
Esta expressão para d é introduzido na expressão obtida na seção anterior para a área. Se forem feitas as substituições e simplificações pertinentes, obtém-se a fórmula que permite calcular a área do heptadecágono:
Área do heptadecágono = (17/2) (rdois) Sen (β) = (17/2) (rdois) Sen (360º / 17)
Uma expressão aproximada para a área é:
Área do heptadecágono = 3,0706 (rdois)
Como esperado, essa área é ligeiramente menor do que a área do círculo que circunscreve o heptadecágono. PARAcirc = π rdois ≈ 3,1416 rdois. Para ser mais preciso, é 2% menor que o de seu círculo circunscrito.
Para que um heptadecágono tenha lados de 2 cm, que valor deve ter o raio e o diâmetro da circunferência circunscrita? Encontre também o valor do perímetro.
Para responder à pergunta, é necessário lembrar a relação entre o lado e o raio de um polígono regular de n lados:
d = 2 r Sen (180º / n)
Para o heptadecágono n = 17, pelo que d = 0,3675 r, ou seja, o raio do heptadecágono é r = 2 cm / 0,3675 = 5,4423 cm ou
10,8844 cm de diâmetro.
O perímetro de um heptadecágono lateral de 2 cm é P = 17 * 2 cm = 34 cm.
Qual é a área de um heptadecágono regular com um lado de 2 cm?
Devemos nos referir à fórmula mostrada na seção anterior, que nos permite encontrar a área de um heptadecágono quando ele tem o comprimento d do seu lado:
Área do heptadecágono = (17/4) (ddois) / Castanho (180º / 17)
Ao substituir d = 2 cm na fórmula acima, você obtém:
Área = 90,94 cm
Ainda sem comentários