
Identidades trigonométricas (exemplos e exercícios)
As identidades trigonométricas são relações entre proporções trigonométricas, que são verdadeiras para qualquer valor da variável. Por exemplo:
tan θ = sin θ / cos θ
É uma identidade trigonométrica que relaciona três razões do ângulo θ, a tangente, o seno e o cosseno do referido ângulo.

Essa identidade é verdadeira para todos os valores, exceto aqueles que tornam 0 o denominador. O cos θ é 0 para θ = ± π / 2, ± 3π / 2, ± 5π / 2 ... Outro exemplo de identidade trigonométrica é:
sin x. sec x. ctg x = 1
Índice do artigo
- 1 demonstração
- 2 tipos de identidades trigonométricas
- 2.1 - Identidades trigonométricas fundamentais
- 2.2 - Identidades pitagóricas
- 2.3 - Fórmulas para o cosseno e seno de adição / subtração de ângulos
- 2.4 - Fórmulas para o ângulo duplo
- 2.5 - Fórmulas para o meio ângulo
- 3 exercícios resolvidos
- 3.1 - Exercício 1
- 3.2 - Exercício 2
- 4 referências
Demonstração
Existem duas maneiras básicas de mostrar que uma identidade trigonométrica é verdadeira:
1- Transformar um dos membros da igualdade no outro, por meio de convenientes manipulações algébricas.
2- Desenvolver ambos os membros da igualdade separadamente, até que as respectivas expressões finais de cada um sejam exatamente as mesmas.
Na identidade proposta, vamos transformar o lado esquerdo da igualdade, para o qual expressamos ctg x e sec x em termos de seno e cosseno da seguinte maneira:
ctg x = cos x / sin x
seg x = 1 / cos x
Substituímos essa expressão no lado esquerdo da identidade e simplificamos:
sin x. (1 / cos x). (cos x / sin x) = (sin x. cos x / cos x. sen x) = 1
E a veracidade da identidade já foi verificada.
Tipos de identidades trigonométricas
Existem várias classes de identidades trigonométricas. Descreveremos resumidamente os principais a seguir:
- Identidades trigonométricas fundamentais
Nós distinguimos dois tipos de identidades fundamentais:
I) Aqueles que são expressos através das relações básicas seno, cosseno e tangente:
- seg x = 1 / cos x
- cosec x / 1 / sin x
- ctg x = 1 / tg x
- tg x = sin x / cos x
- ctg x = cos x / sin x
II) As derivadas de paridade. Sabemos por seu gráfico que sin x é uma função ímpar, o que significa que:
sin (-x) = - sin x
Por sua vez, cos x é uma função par, portanto:
cos (-x) = cos x
Então:
tg (-x) = sin (-x) / cos (-x) = -sen x / cos x
Igualmente:
- cotg (-x) = -ctg x
- seg (-x) = seg x
- cosec (-x) = - cosec x
- Identidades pitagóricas
Eles são obtidos a partir da aplicação do teorema de Pitágoras ao triângulo retângulo das pernas aeb e à hipotenusa c. Vamos ver:
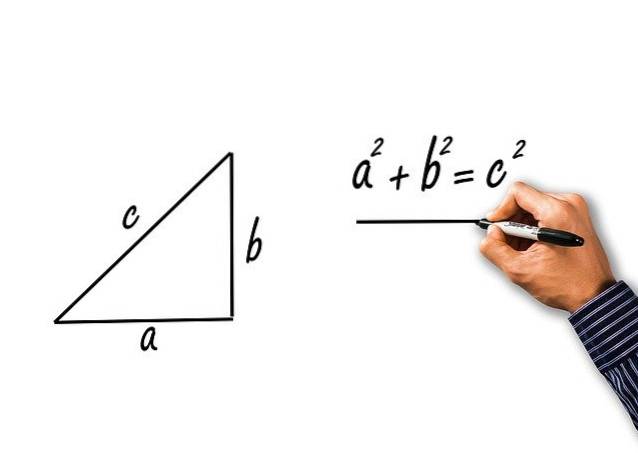
O teorema de Pitágoras afirma que:
cdois = adois + bdois
Dividindo tudo por cdois:
cdois / cdois = (adois / cdois) + (Bdois / cdois)
O termo à esquerda é 1 e lembrando que o seno e o cosseno do ângulo agudo α são definidos como:
sin α = a / c
cos α = b / c
Resultado:
1 = (sin α)dois + (cos α)dois
Esta identidade é conhecida como identidade fundamental.
O procedimento pode ser realizado dividindo-se por umdois e Bdois, o que dá origem a mais duas identidades:
sdois α = 1 + tgdois α
colheitadois α = 1 + ctgdois α
- Fórmulas para o cosseno e seno da adição / subtração de ângulos
As principais identidades trigonométricas para cosseno, seno e tangente de adição e subtração são as seguintes:


Prova de pecado (α + β) e cos (α + β)
Essas identidades podem ser comprovadas geometricamente ou também pela fórmula de Euler:
eiα = cos α + i sen α
Vamos ver o que acontece com a fórmula ao substituir a soma de dois ângulos α e β:
ei (α +β) = cos (α + β) + i sen (α + β)
Esta expressão é complexa, sua parte real é cos (α + β) e sua parte imaginária é i sin (α + β). Guardamos este resultado para uso posterior e nos concentramos no desenvolvimento da parte exponencial:
ei (α +β) = eiα ⋅ eiβ = (cos α + i sen α). (cos β + i sen β) =
= cos α⋅cos β + cos α⋅i sen β + i⋅sen α cos β - sen α⋅sen β
A parte real desta expressão é aquela que não é multiplicada pela unidade imaginária "i":
cos α⋅cos β - sen α. sin β
A parte imaginária, portanto, é:
i (cos α⋅sen β + sin α⋅cos β)
Para que duas expressões complexas sejam iguais, a parte real de uma deve ser igual à parte real da outra. O mesmo acontece com as partes imaginárias.
Pegamos o resultado salvo e o comparamos com este:
cos α. cos β - sen α. sin β = cos (α + β)
i (cos α⋅sen β + sin α⋅cos β) = i sin (α + β)
sin (α + β) = (cos α. sin β + sin α⋅cos β)
- Fórmulas para o ângulo duplo
Nas fórmulas anteriores, pegamos β = α e desenvolvemos:
sin (α + α) = sin 2 α = sin α⋅cos α + cos α. sin α = 2⋅ sin α ⋅ cos α
cos (α + α) = cos 2 α = cos α⋅cos α - sen α⋅sen α = cosdois α - pecado dois α
tg (α + α) = tg 2 α = [tg α + tg α] / [1- tg α⋅tg α] = 2tg α / 1- tgdois α
Se na segunda expressão substituirmos cosdois α = 1 - pecadodois α é obtido:
cos 2 α = cosdois α - (1- cosdois α) = 2 cosdois α -1
- Fórmulas para o meio ângulo
Nesta última expressão, vamos substituir α / 2 por α, o seguinte permanece:
cos α = 2 cos dois(α / 2) -1
Resolvendo para:


Exercícios resolvidos
- Exercício 1
Mostre que:

Vamos trabalhar o termo esquerdo algebricamente para que se pareça com o direito. Uma vez que sin x aparece no termo certo, a primeira etapa é expressar cosdoisx em termos de sen x de modo que tudo esteja em termos da mesma razão trigonométrica:
Então 1 - o pecado é fatoradodois x porque é uma diferença de quadrados perfeitos. Para fazer isso, ele limpa a identidade fundamental:
porquedoisx = 1 - pecadodois x
1 - sendois x = (1- sen x) (1 + senx)
E a fatoração é substituída na expressão original:

O termo (1-senx) é simplificado e uma igualdade permanece:
1 + sen x = 1 + senx
- Exercício 2
Resolva a seguinte equação trigonométrica e dê a solução para valores entre 0 e 360º:
tg x + segdois x = 3
Solução
No termo da esquerda existem duas relações trigonométricas, portanto é necessário reduzir tudo a uma única, para podermos resolver o desconhecido. O termo secdois x é expresso por meio de uma das identidades pitagóricas:
sdois α = 1 + tgdois α
A substituição na equação permanece:
tg x + 1 + tgdois x = 3
Reorganizando os termos:
tgdois x + tg x + 1 = 3
Esta equação é resolvida fazendo a mudança da variável:
tg x = u
oudois + u + 1 - 3 = 0 → udois + u - 2 = 0
Esta equação quadrática é facilmente resolvida pela fatoração:
(u +2) (u-1) = 0
Portanto você1 = -2 e udois = 1, que é equivalente a:
tg x1 = -2
tg xdois = 1
Finalmente:
x1 = arctg (-2) = 296,6º
xdois = arctg (1) = 45º
Referências
- Carena, M. 2019. Manual de Matemática Pré-Universitária. Universidade Nacional do Litoral.
- Figuera, J. 1999. Mathematics. 1ª Diversificado. Bolivarian Collegiate Editions.
- Hoffman, J. Selection of Mathematics Topics. Volume 4.
- Jiménez, R. 2008. Algebra. Prentice Hall.
- Wikipedia. Identidades e fórmulas trigonométricas. Recuperado de: es.wikipedia.org.
- Zapata, F. 4 maneiras de resolver uma equação quadrática. Recuperado de: francesphysics.blogspot.com.
- Zill, D. 1984. Algebra and Trigonometry. Colina Mcgraw.



Ainda sem comentários