
Fórmulas de indução magnética, como é calculado e exemplos
O indução magnética ou a densidade do fluxo magnético é uma alteração do ambiente causada pela presença de correntes elétricas. Eles modificam a natureza do espaço que os rodeia, criando um campo vetor.
O vetor indução magnética, densidade de fluxo magnético ou simplesmente campo magnético B, tem três características distintas: uma intensidade expressa por um valor numérico, uma direção e também um sentido dado em cada ponto do espaço. É destacado em negrito para distingui-lo de quantidades puramente numéricas ou escalares.
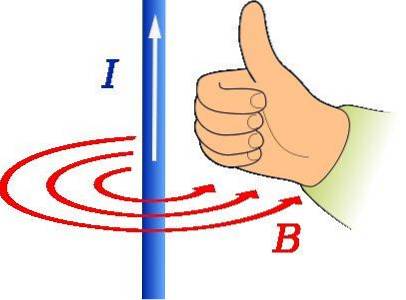
A regra do polegar direito é usada para encontrar a direção e direção do campo magnético causado por um fio condutor de corrente, conforme mostrado na figura acima.
O polegar da mão direita deve apontar na direção da corrente. Em seguida, a rotação dos quatro dedos restantes indica a forma de B, que na figura é representado pelos círculos vermelhos concêntricos.
Nesse caso, o endereço de B é tangencial à circunferência concêntrica com o fio e é no sentido anti-horário.
O indução magnética B No Sistema Internacional, Tesla (T) é medido, porém é mais frequente medi-lo em outra unidade chamada Gauss (G). Ambas as unidades foram nomeadas respectivamente em homenagem a Nikola Tesla (1856-1943) e Carl Friedrich Gauss (1777-1855) por suas contribuições extraordinárias para a ciência da eletricidade e do magnetismo..
Índice do artigo
- 1 Quais são as propriedades de indução magnética ou densidade de fluxo magnético?
- 2 Lei de Biot-Savart
- 3 fórmulas
- 4 Como é calculado?
- 4.1 Exemplo
- 5 referências
Quais são as propriedades de indução magnética ou densidade de fluxo magnético?
Uma bússola colocada perto do fio energizado sempre se alinhará com B. O físico dinamarquês Hans Christian Oersted (1777-1851) foi o primeiro a notar esse fenômeno no início do século 19.
E quando a corrente cessa, a bússola aponta novamente para o norte geográfico, como sempre. Mudando cuidadosamente a posição da bússola, um mapa da forma do campo magnético é obtido.
Este mapa tem sempre a forma de círculos concêntricos ao fio, conforme descrito no início. Desta forma, você pode visualizar B.
Mesmo que o fio não seja reto, o vetor B ele formará círculos concêntricos ao seu redor. Para determinar a forma do campo, imagine apenas segmentos muito pequenos de arame, tão pequenos que parecem retilíneos e circundados por círculos concêntricos..
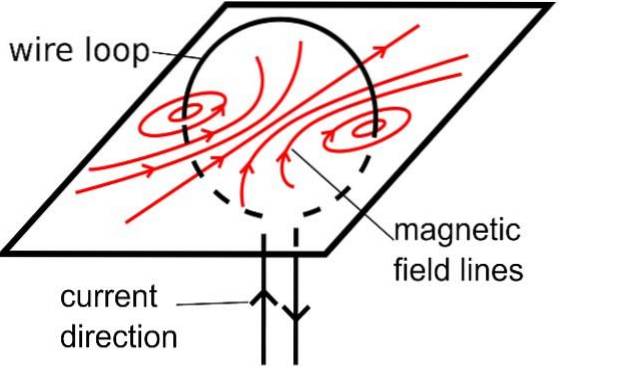
Isso aponta para uma propriedade importante das linhas do campo magnético. B: não têm começo nem fim, são sempre curvas fechadas.
Lei de Biot-Savart
O século 19 marcou o início da era da Eletricidade e do Magnetismo na ciência. Por volta do ano de 1820, os físicos franceses Jean Marie Biot (1774-1862) e Felix Savart (1791-1841) descobriram a lei que leva seu nome e que nos permite calcular o vetor B.
Eles fizeram as seguintes observações sobre a contribuição para o campo magnético produzido por um segmento de fio de comprimento diferencial dl que carrega uma corrente elétrica eu:
- A magnitude de B diminui com o inverso do quadrado da distância até o fio (isso faz sentido: longe do fio a intensidade de B deve ser menor do que pontos próximos).
- A magnitude de B é proporcional à intensidade da corrente eu que passa pelo fio.
- O endereço de B é tangencial à circunferência do raio r centrado no fio e no sentido de B é dado, como dissemos, pela regra do polegar direito.
O produto vetorial ou produto vetorial é a ferramenta matemática apropriada para expressar o último ponto. Para estabelecer um produto vetorial, são necessários dois vetores, que são definidos da seguinte forma:
- deu é o vetor cuja magnitude é o comprimento do segmento diferencial dl
- r é o vetor que vai do fio ao ponto onde você deseja encontrar o campo
Fórmulas
Tudo isso pode ser combinado em uma expressão matemática:

A constante de proporcionalidade necessária para estabelecer a igualdade é a permeabilidade magnética do espaço livre μou = 4π.10-7 T.m / A
Esta expressão é a lei de Biot e Savart, que nos permite calcular o campo magnético de um segmento de corrente..
Esse segmento, por sua vez, deve fazer parte de um circuito maior e mais fechado: uma distribuição de corrente.
A condição de o circuito estar fechado é necessária para que uma corrente elétrica flua. A corrente elétrica não pode fluir em circuitos abertos.
Finalmente, para encontrar o campo magnético total da referida distribuição de corrente, todas as contribuições de cada segmento diferencial são adicionadas deu. Isso é equivalente a integração em toda a distribuição:

Para aplicar a lei de Biot-Savart e calcular o vetor de indução magnética, é necessário considerar alguns pontos muito importantes:
- O produto cruzado entre dois vetores sempre resulta em outro vetor.

- É conveniente encontrar o produto vetorial antes para passar à resolução do integral, então o integral de cada um dos componentes obtidos separadamente é resolvido.
- É necessário traçar um quadro da situação e estabelecer um sistema de coordenadas adequado.
- Sempre que for observada a existência de alguma simetria, ela deve ser utilizada para economizar tempo de cálculo.
- Quando existem triângulos, o teorema de Pitágoras e o teorema do cosseno são de grande ajuda para estabelecer a relação geométrica entre as variáveis..
Como é calculado?
Com um exemplo prático do cálculo de B para um fio reto, essas recomendações se aplicam.
Exemplo
Calcule o vetor de campo magnético que um fio retilíneo muito longo produz em um ponto P no espaço, de acordo com a figura mostrada.

A partir da figura, você deve:
- O fio é direcionado na direção vertical, com a corrente I fluindo para cima. Esta direção é + y no sistema de coordenadas, cuja origem está no ponto O.
- Nesse caso, de acordo com a regra do polegar direito, B no ponto P é direcionado para o interior do papel, por isso é denotado por um pequeno círculo e um “x” na figura. Este endereço será tomado como -z.
- O triângulo retângulo cujas pernas são Y Y R, relacionar ambas as variáveis de acordo com o teorema de Pitágoras: rdois= Rdois+Ydois
Tudo isso é substituído no integral. O produto vetorial ou cruz é indicado por sua magnitude mais sua direção e seu sentido:
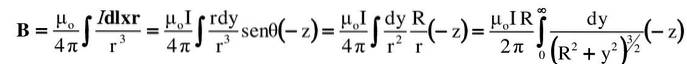
A integral proposta é encontrada em uma tabela de integrais ou é resolvida por uma substituição trigonométrica apropriada (o leitor pode verificar o resultado usando y = Rtg θ):
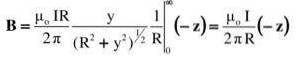
O resultado está de acordo com o que era esperado: a magnitude do campo diminui com a distância R e aumenta proporcionalmente com a intensidade da corrente I.
Embora um fio infinitamente longo seja uma idealização, a expressão obtida é uma boa aproximação para o campo de um fio longo..
Com a lei de Biot e Savart é possível encontrar o campo magnético de outras distribuições altamente simétricas, como um loop circular que transporta corrente, ou fios tortos combinando segmentos retilíneos e curvilíneos..
Obviamente, para resolver analiticamente a integral proposta, o problema deve ter um alto grau de simetria. Caso contrário, a alternativa é resolver numericamente a integral.
Referências
- Serway, R., Jewett, J. (2008). Física para Ciências e Engenharia. Volume 2. México. Editores do Cengage Learning. 367-372.



Ainda sem comentários