O Lei Beer-Lambert (Beer-Bouguer) é aquele que relaciona a absorção da radiação eletromagnética de uma ou mais espécies químicas, com sua concentração e a distância que a luz percorre nas interações partícula-fóton. Esta lei reúne duas leis em uma.
A lei de Bouguer (embora o reconhecimento tenha recaído mais sobre Heinrich Lambert), estabelece que uma amostra absorverá mais radiação quando as dimensões do meio ou material absorvente forem maiores; especificamente, sua espessura, que é a distância eu que a luz viaja ao entrar e sair.
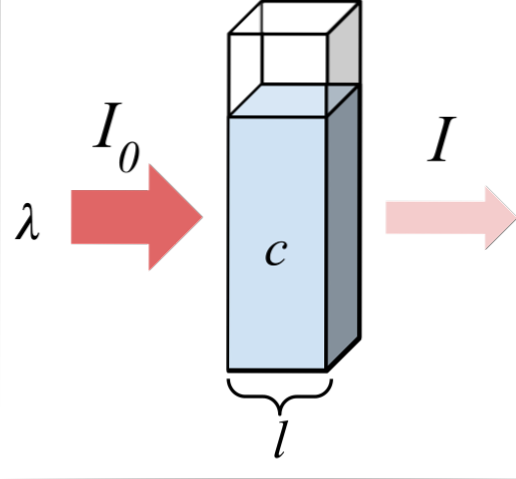
A imagem superior mostra a absorção da radiação monocromática; isto é, feito de um único comprimento de onda, λ. O meio absorvente está dentro de uma célula óptica, cuja espessura é eu, e contém espécies químicas com uma concentração c.
O feixe de luz tem uma intensidade inicial e final, designada pelos símbolos I0 e eu, respectivamente. Observe que depois de interagir com o meio absorvente, I é menor que I0, o que mostra que houve absorção de radiação. Quanto mais velhos eles são c Y eu, menor serei eu em relação a mim0; ou seja, haverá mais absorção e menos transmitância.
Índice do artigo
A imagem acima engloba perfeitamente esta lei. A absorção de radiação em uma amostra aumenta ou diminui exponencialmente em função de c ou eu. Para compreender plena e facilmente a lei, é necessário contornar seus aspectos matemáticos.
Como acabei de mencionar, eu0 e I são as intensidades do feixe de luz monocromático antes e depois da luz, respectivamente. Alguns textos preferem usar os símbolos P0 e P, que se referem à energia da radiação e não à sua intensidade. Aqui, a explicação será continuada usando as intensidades.
Para linearizar a equação desta lei, deve-se aplicar o logaritmo, geralmente a base 10:
Log (I0/ I) = εlc
O termo (eu0/ I) indica o quanto a intensidade do produto de radiação de absorção diminui. A lei de Lambert considera apenas l (εl), enquanto a lei de Beer ignora l, mas coloca c em vez disso (εc) A equação superior é a união de ambas as leis e, portanto, é a expressão matemática geral para a lei de Beer-Lambert.
A absorbância é definida pelo termo Log (I0/ EU). Assim, a equação é expressa da seguinte forma:
A = εlc
Onde ε é o coeficiente de extinção ou absortividade molar, que é uma constante em um determinado comprimento de onda.
Observe que se a espessura do meio absorvente for mantida constante, como ε, a absorbância A dependerá apenas da concentração c, de espécies absorventes. Além disso, é uma equação linear, y = mx, onde Y é A, e x isso é c.
À medida que a absorbância aumenta, a transmitância diminui; isto é, quanta radiação consegue ser transmitida após a absorção. Eles são, portanto, inversos. sim eu0/ I indica o grau de absorção, I / I0 é igual a transmitância. Sabendo disso:
Eu / eu0 = T
(EU0/ I) = 1 / T
Log (I0/ I) = Log (1 / T)
Mas, Log (eu0/ I) também é igual à absorbância. Portanto, a relação entre A e T é:
A = Log (1 / T)
E aplicando as propriedades dos logaritmos e sabendo que Log1 é igual a 0:
A = -LogT
As transmitâncias são geralmente expressas em porcentagens:
% T = I / I0∙ 100
Como afirmado anteriormente, as equações correspondem a uma função linear; portanto, espera-se que, ao representá-los, eles forneçam uma linha.
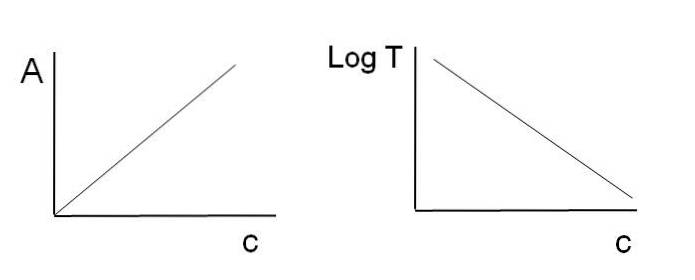
Observe que à esquerda da imagem acima está a linha obtida pelo gráfico de A em relação c, e à direita a linha correspondente ao gráfico de LogT contra c. Um tem inclinação positiva e o outro negativo; quanto maior a absorbância, menor a transmitância.
Graças a essa linearidade, a concentração das espécies químicas absorventes (cromóforos) pode ser determinada se for conhecida a quantidade de radiação que elas absorvem (A), ou a quantidade de radiação transmitida (LogT). Quando esta linearidade não é observada, diz-se que está enfrentando um desvio, positivo ou negativo, da lei de Beer-Lambert..
Em termos gerais, algumas das aplicações mais importantes desta lei são mencionadas abaixo:
-Se uma espécie química apresenta cor, é um candidato exemplar a ser analisado por técnicas colorimétricas. Estes baseiam-se na lei de Beer-Lambert e permitem determinar a concentração dos analitos em função das absorbâncias obtidas em espectrofotômetro..
-Permite a construção de curvas de calibração, com as quais, levando em consideração o efeito de matriz da amostra, é determinada a concentração da espécie de interesse..
-É amplamente utilizado para análise de proteínas, pois vários aminoácidos possuem absorções significativas na região ultravioleta do espectro eletromagnético..
-Reações químicas ou fenômenos moleculares que envolvem uma mudança na cor podem ser analisados usando valores de absorbância em um ou mais comprimentos de onda..
-Usando análise multivariada, misturas complexas de cromóforos podem ser analisadas. Desta forma, a concentração de todos os analitos pode ser determinada, e também, as misturas podem ser classificadas e diferenciadas umas das outras; por exemplo, descartar se dois minerais idênticos vêm do mesmo continente ou país específico.
Qual é a absorbância de uma solução exibindo uma transmitância de 30% em um comprimento de onda de 640 nm??
Para resolvê-lo, basta ir às definições de absorbância e transmitância.
% T = 30
T = (30/100) = 0,3
E sabendo que A = -LogT, o cálculo é direto:
A = -Log 0,3 = 0,5228
Observe que faltam unidades.
Se a solução do exercício anterior consiste em uma espécie W cuja concentração é 2,30 ∙ 10-4 M, e supondo que a célula tenha 2 cm de espessura: qual deve ser sua concentração para obter uma transmitância de 8%??
Isso poderia ser resolvido diretamente com esta equação:
-LogT = εlc
Mas, o valor de ε é desconhecido. Portanto, deve ser calculado com os dados anteriores e pressupõe-se que permaneça constante em uma ampla faixa de concentrações:
ε = -LogT / lc
= (-Log 0,3) / (2 cm x 2,3 ∙ 10-4 M)
= 1136,52 M-1∙ cm-1
E agora, você pode prosseguir para o cálculo com% T = 8:
c = -LogT / εl
= (-Log 0,08) / (1136,52 M-1∙ cm-1 x 2cm)
= 4,82 ∙ 10-4 M
Então, basta que a espécie W dobre sua concentração (4,82 / 2,3) para reduzir sua porcentagem de transmitância de 30% para 8%..
Ainda sem comentários