
Fórmula da lei de Faraday, unidades, experimentos, exercícios,
O Lei de faraday no eletromagnetismo afirma que um fluxo de campo magnético variável é capaz de induzir uma corrente elétrica em um circuito fechado.
Em 1831, o físico inglês Michael Faraday fez experiências com condutores móveis dentro de um campo magnético e também com campos magnéticos variáveis que passavam por condutores fixos..
Faraday percebeu que se variasse o fluxo do campo magnético ao longo do tempo, ele seria capaz de estabelecer uma voltagem proporcional a essa variação. Se ε é a tensão ou força eletromotriz induzida (fem induzida) e Φ é o fluxo do campo magnético, na forma matemática pode ser expresso:
| ε | = ΔΦ / Δt
Onde o símbolo Δ indica variação da quantidade e as barras na fem indicam o valor absoluto desta. Por ser um circuito fechado, a corrente pode fluir em uma direção ou na outra.
O fluxo magnético, produzido por um campo magnético em uma superfície, pode variar de várias maneiras, por exemplo:
-Movendo uma barra magnética através de um laço circular.
-Aumentar ou diminuir a intensidade do campo magnético que passa pelo circuito.
-Deixando o campo fixo, mas por meio de algum mecanismo alterar a área do loop.
-Combinando os métodos acima.

Índice do artigo
- 1 Fórmulas e unidades
- 1.1 Lei de Lenz
- 2 experimentos Faraday
- 2.1 Variação do fluxo magnético por rotação
- 3 referências
Fórmulas e unidades
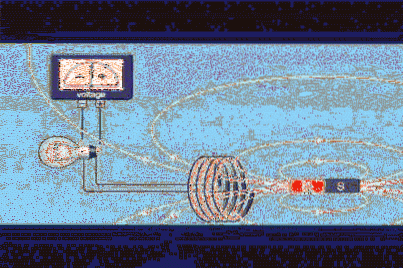
Suponha que você tenha um circuito fechado de área A, como um loop circular ou enrolamento igual ao da figura 1, e que você tenha um ímã que produz um campo magnético B.
O fluxo do campo magnético Φ é uma quantidade escalar que se refere ao número de linhas de campo que cruzam a área A. Na figura 1 estão as linhas brancas que saem do pólo norte do ímã e retornam pelo sul.
A intensidade do campo será proporcional ao número de linhas por unidade de área, então podemos ver que nos pólos é muito intenso. Mas podemos ter um campo muito intenso que não produz fluxo no loop, o que podemos alcançar mudando a orientação deste (ou do ímã).
Para levar em consideração o fator de orientação, o fluxo do campo magnético é definido como o produto escalar entre B Y n, sendo n o vetor normal unitário à superfície do loop e que indica sua orientação:
Φ = B•n A = BA.cosθ
Onde θ é o ângulo entre B Y n. Se por exemplo B Y n são perpendiculares, o fluxo do campo magnético é zero, pois nesse caso o campo é tangente ao plano do loop e não pode passar por sua superfície.
Ao invés sim B Y n são paralelos, significa que o campo é perpendicular ao plano do loop e as linhas passam por ele o mais longe possível.
A unidade no Sistema Internacional para F é o weber (W), onde 1 W = 1 T.mdois (leia "tesla por metro quadrado").
Lei de Lenz
Na figura 1, podemos ver que a polaridade da voltagem muda conforme o ímã se move. A polaridade é estabelecida pela lei de Lenz, que estabelece que a tensão induzida deve se opor à variação que a produz.
Se, por exemplo, o fluxo magnético produzido pelo ímã aumenta, uma corrente é estabelecida no condutor que circula criando seu próprio fluxo, que se opõe a esse aumento..
Se, pelo contrário, o fluxo gerado pelo íman diminui, a corrente induzida circula de forma que o seu próprio fluxo neutraliza essa diminuição..
Para levar em conta este fenômeno, um sinal negativo é colocado antes da lei de Faraday e não é mais necessário colocar as barras de valor absoluto:
ε = -ΔΦ / Δt
Esta é a lei Faraday-Lenz. Se a variação do fluxo for infinitesimal, os deltas são substituídos por diferenciais:
ε = -dΦ / dt
A equação acima é válida para um loop. Mas se tivermos uma bobina de N voltas, o resultado é muito melhor, porque a fem é multiplicada por N vezes:
ε = - N (dΦ / dt)
Experimentos Faraday
Para que a corrente ligue a lâmpada a ser produzida, deve haver um movimento relativo entre o ímã e o laço. Esta é uma das formas em que o fluxo pode variar, pois desta forma muda a intensidade do campo que passa pelo loop..
Assim que o movimento do ímã cessa, a lâmpada apaga-se, mesmo que o ímã fique parado no meio do laço. O que é necessário para fazer circular a corrente que liga a lâmpada é que o fluxo do campo varie.
Quando o campo magnético varia com o tempo, podemos expressá-lo como:
B = B (t).
Mantendo constante a área A do loop e deixando-a fixa em um ângulo constante, que no caso da figura é 0º, então:


Se for possível alterar a área do loop, deixando sua orientação fixa e colocando-a no meio de um campo constante, a fem induzida é dada por:

Uma maneira de conseguir isso é colocar uma barra que desliza em um trilho condutor a uma determinada velocidade, conforme mostrado na figura a seguir.

A barra e o trilho, mais uma lâmpada ou um resistor conectado com fios condutores, formam um circuito fechado em forma de loop retangular..
Ao deslizar a barra, o comprimento x aumenta ou diminui, e com isso a área do loop muda, o que é suficiente para criar um fluxo variável.
Variação do fluxo magnético por rotação
Como dissemos antes, se o ângulo entre B e o normal do loop é feito para variar, o fluxo de campo muda de acordo com:
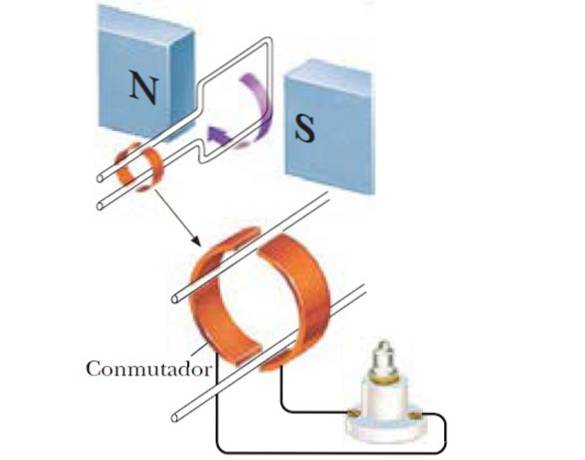

Assim, um gerador senoidal é obtido, e se em vez de uma única bobina um número N de bobinas são usados, a fem induzida é maior:


Uma bobina circular de N voltas e raio R, gira com frequência angular ω no meio de um campo magnético de magnitude B. Encontre uma expressão para a fem máxima induzida na bobina.
Solução
A expressão para a fem induzida pela rotação é aplicada quando a bobina tem N voltas, sabendo que:
-A área da bobina é A = πRdois
-O ângulo θ varia em função do tempo, pois θ = ωt
É importante notar que primeiro θ = ωt é substituído na lei de Faraday e em breve é derivado em relação ao tempo:
ε = -NBA (cos θ) '= -NB (πRdois). [cos (ωt)] '= NBω (πRdois) sin (ωt)
Uma vez que a fem máxima é solicitada, ela ocorre sempre que sin ωt = 1, então finalmente:
εmax = NBω (πRdois)
Referências
- Figueroa, D. 2005. Série: Física para Ciências e Engenharia. Volume 6. Eletromagnetismo. Editado por Douglas Figueroa (USB).
- Giambattista, A. 2010. Física. Segunda edição. Colina Mcgraw.
- Giancoli, D. 2006. Física: Princípios com Aplicações. 6º. Ed. Prentice Hall.
- Resnick, R. 1999. Physics. Vol. 2. 3ª Ed. Em espanhol. Compañía Editorial Continental S.A. por C.V.
- Sears, Zemansky. 2016. Física Universitária com Física Moderna. 14º. Ed. Volume 2.



Ainda sem comentários