
Lei de gauss

Qual é a lei de Gauss?
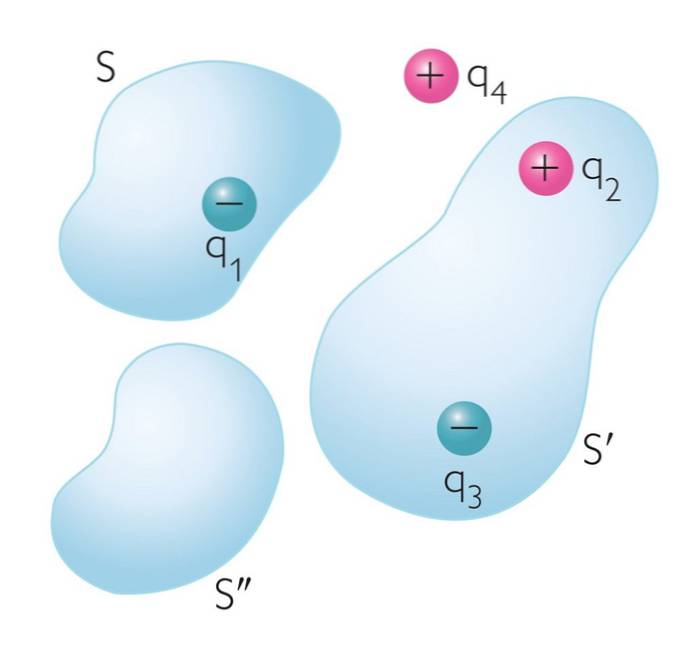
O lei de gauss estabelece que o fluxo do campo elétrico através de uma superfície fechada imaginária é proporcional ao valor líquido de carga das partículas encontradas dentro da referida superfície.
Denotando o fluxo elétrico através de uma superfície fechada como ΦE e a carga líquida envolvida pela superfície por Qenc, então, a seguinte relação matemática é estabelecida:
ΦE = c ∙ Qenc
Onde c é a constante de proporcionalidade.
Explicação da lei de Gauss
Para entender o significado da lei de Gauss, é necessário explicar os conceitos envolvidos em sua afirmação: carga elétrica, campo elétrico e fluxo do campo elétrico através de uma superfície..
Carga elétrica
A carga elétrica é uma das propriedades fundamentais da matéria. Um objeto carregado pode ter um dos dois tipos de carga: positiva ou negativa, embora normalmente os objetos sejam neutros, ou seja, possuem a mesma quantidade de carga negativa que positiva..
Dois objetos carregados do mesmo tipo se repelem mesmo quando não há contato entre eles e eles estão no vácuo. Ao contrário, quando cada um dos corpos tem cargas de signos diferentes, eles se atraem. Esse tipo de interação à distância é conhecido como interação elétrica..
No sistema internacional de unidades SI, a carga elétrica é medida em coulombs (C). O portador de carga elementar negativa é o elétron com carga de -1,6 x 10-19C e o portador de carga elementar positivo é o próton com um valor de carga +1,6 x 10-19C. Corpos normalmente carregados têm entre 10-9C Y 10-3C.
Campo elétrico
Um corpo eletricamente carregado altera o espaço em seu ambiente, preenchendo-o com algo invisível chamado campo elétrico. Para saber que este campo está presente, é necessária uma carga de ponto de teste positiva.
Se a carga de teste é colocada em um local onde existe um campo elétrico, uma força aparece sobre ela em uma determinada direção, que é a mesma do campo elétrico. A intensidade do campo é a força da carga de teste dividida pela quantidade de carga da carga de teste. Então, as unidades do campo elétrico E no Sistema Internacional de unidades são Newton Entre coulomb: [E] = N / C.
Cargas pontuais positivas produzem um campo radial externo, enquanto cargas negativas produzem um campo radial interno. Além disso, o campo produzido por uma carga pontual decai com o inverso do quadrado da distância até a referida carga.
Linhas de campo elétrico
Michael Faraday (1791 - 1867) foi o primeiro a ter uma imagem mental do campo elétrico, imaginando-o como linhas que seguem a direção do campo. No caso de uma carga pontual positiva, essas linhas são radiais a partir do centro para fora. Onde as linhas estão mais próximas, o campo é mais intenso e menos intenso onde elas estão mais afastadas.
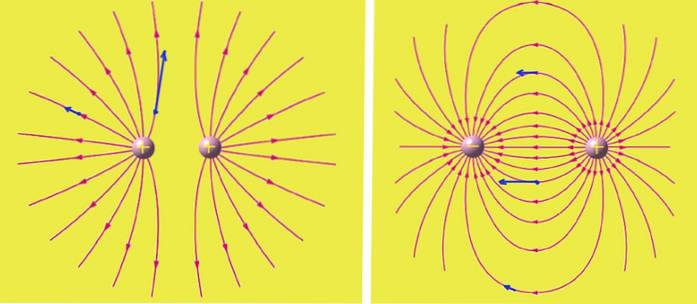
Cargas positivas são as fontes de onde emergem as linhas de campo elétrico, enquanto as cargas negativas são os sumidouros das linhas..
As linhas de campo elétrico não se fecham sobre si mesmas. Num conjunto de cargas as linhas saem das cargas positivas e entram nas positivas, mas também podem chegar ou vir do infinito.
Eles também não se cruzam e em cada ponto no espaço o vetor do campo elétrico é tangente à linha do campo e proporcional à densidade das linhas ali..

Fluxo de campo elétrico
As linhas de campo elétrico se assemelham às linhas de corrente de um rio que flui suavemente, daí o conceito de fluxo de campo elétrico ter nascido..
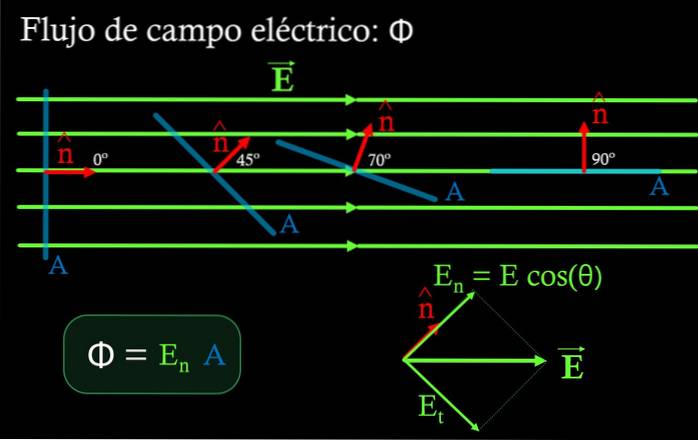
Em uma região onde o campo elétrico é uniforme, o fluxo Φ através de uma superfície plana é o produto da componente normal do campo En a esta superfície, multiplicado pela área PARA da mesma:
Φ = En ∙ A
Componente En é obtido multiplicando a magnitude do campo elétrico pelo cosseno do ângulo formado entre o campo e o vetor normal da unidade para a área de superfície PARA. (veja a figura 4).
Aplicações da lei de Gauss
A lei de Gauss pode ser aplicada para determinar o campo elétrico produzido por distribuições de carga com um alto grau de simetria.
Campo elétrico de uma carga pontual
Uma carga pontual produz um campo elétrico radial que sai se a carga for positiva e entra em caso contrário..
Escolhendo como superfície gaussiana uma esfera imaginária de raio R e concêntrica à carga Q, em todos os pontos da superfície dessa esfera o campo elétrico é de igual magnitude e sua direção é sempre normal à superfície. Portanto, neste caso, o fluxo do campo elétrico é o produto da magnitude do campo e da área total da superfície esférica:
Φ = E ∙ A = E ∙ 4πRdois
Por outro lado, a lei de Gauss afirma que: Φ = c ∙ Q, sendo a constante de proporcionalidade c. Ao trabalhar em unidades do sistema de medição internacional, a constante c é o inverso da permissividade do vácuo, e a lei de Gauss é formulada assim:
Φ = (1 / εou) ∙ Q
Incorporando o resultado obtido para o fluxo à lei de Gauss, temos:
E ∙ 4πRdois = (1 / εou) ∙ Q
E pela magnitude de E resultado:
E = (1 / 4πεou) ∙ (Q / Rdois)
O que concorda totalmente com a lei de Coulomb do campo elétrico de uma carga pontual.
Treinamento
Exercício 1
Duas cargas pontuais ficam dentro de uma superfície gaussiana S arbitrariamente. Um deles é conhecido por ter um valor de +3 nC (3 nano-coulomb). Se o fluxo líquido do campo elétrico através da superfície gaussiana for 113 (N / C) mdois, Qual será o valor da outra carga?
Solução
A lei de Gauss afirma que
ΦE = (1 / εou) ∙ Qenc
Portanto, a carga líquida incluída é:
Qenc = ΦE ∙ εou
Substituindo os resultados dos dados:
Qenc = 113 (N / C) mdois ∙ 8,85 x 10-12 (Cdois m-dois N-1) = 1 x 10-9 C = 1 nC.
Mas Qenc = + Q - q, onde a carga positiva tem um valor conhecido de +3 nC, portanto, a carga será necessariamente -2 nC.
Exercício 2
Na figura 2 há um arranjo (à esquerda) de duas cargas positivas, cada uma com um valor + q e outro arranjo (à direita) com uma carga + q e a outra -q. Cada arranjo é encerrado em uma caixa imaginária com todas as suas bordas de 10 cm. Se | q | = 3 μC, encontre o fluxo do campo elétrico líquido através da caixa para cada arranjo.
Solução
No primeiro arranjo, o fluxo líquido é:
ΦE = (1 / εou) ∙ (+ q + q) = 678000 (N / C) mdois
No arranjo da direita, o fluxo líquido através da caixa imaginária contendo o par de cargas é zero..
Referências
- Cosenza, M. Electromagnetism. Universidade dos Andes.
- Díaz, R. Eletrodinâmica: notas de aula. universidade nacional da Colômbia.
- Figueroa, D. (2005). Série: Física para Ciência e Engenharia. Volume 6. Eletromagnetismo. Editado por Douglas Figueroa (USB).
- Jackson, J. D. Classical Electrodynamics. 3º. Ed. Wiley.
- Tarazona, C. Introdução à Eletrodinâmica. Editorial Universidade Manuela Beltrán.



Ainda sem comentários