
Fórmulas, exemplos, aplicações, exercícios da lei de Hooke
O Lei de Hooke destaca que a deformação experimentada por um objeto elástico é diretamente proporcional à força aplicada a ele. A constante de proporcionalidade depende da natureza do objeto, de sua geometria e do material com o qual é feito..
Todos os materiais têm propriedades elásticas em maior ou menor grau, de modo que cumprem a lei de Hooke desde que retornem às suas dimensões originais, uma vez que a força cesse. Molas e elásticos são bons exemplos de objetos que atendem à lei de Hooke, mas também são pinos de aço que fazem parte de uma ponte.

Tomando uma mola ou mola como exemplo, para mantê-la esticada ou comprimida, é necessário aplicar uma força de magnitude F. Segundo a lei de Hooke, a mola sofrerá uma deformação x:
F ∝ x
A constante de proporcionalidade, que por ser uma mola é chamada rigidez da mola constante, é denotado como k, portanto:
F = k⋅x
Nas unidades do Sistema Internacional, a força está em newtons (N) e a deformação em metros (m). Portanto, a constante da mola tem unidades de N / m. A constante da mola representa a força que deve ser aplicada para deformá-la em 1 m de comprimento.
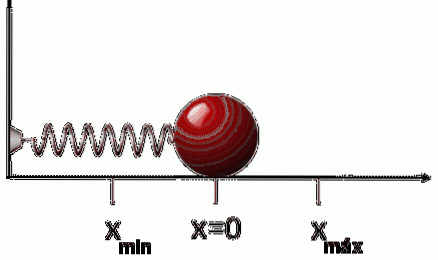
Se, após esticar ou comprimir a mola, ela for liberada, ela se moverá na direção oposta à força aplicada. Isso significa que se esticarmos, ele comprime e vice-versa. Daí a força FR o que a primavera exerce isso é:
FR = -k⋅x
O sinal negativo indica o referido: que a força se opõe ao deslocamento, portanto essa força é conhecida como força restauradora.
Índice do artigo
- 1 Fórmula e equações
- 1.1 Trabalho feito para esticar ou comprimir uma mola
- 2 exemplos de molas
- 2.1 Mola de compressão
- 2.2 Molas de extensão e torção
- 2.3 Materiais para fazer molas
- 3 Aplicações da Lei de Hooke
- 4 exercícios resolvidos
- 4.1 - Exercício 1
- 4.2 - Exercício 2
- 5 referências
Fórmula e equações
A relação entre força e deslocamento em uma mola foi descoberta por Robert Hooke (1635-1703), notável físico inglês conhecido por sua rivalidade com Isaac Newton. Hooke foi um cientista versátil que se aventurou com sucesso em diferentes campos da ciência: mecânica, biologia, astronomia e arquitetura..

Hooke percebeu que se a força aplicada a uma mola não for muito grande, a mola se deforma proporcionalmente à força e, uma vez que essa força desaparece, a mola retorna ao seu comprimento natural.
Assim, a lei de Hooke na forma gráfica é na forma de uma linha reta, a inclinação da qual é a constante da mola. A imagem a seguir mostra a força exercida na mola para esticá-la - ou comprimi-la - em função da posição x. Observe também que a força não depende do comprimento natural da mola, mas de seu deslocamento..
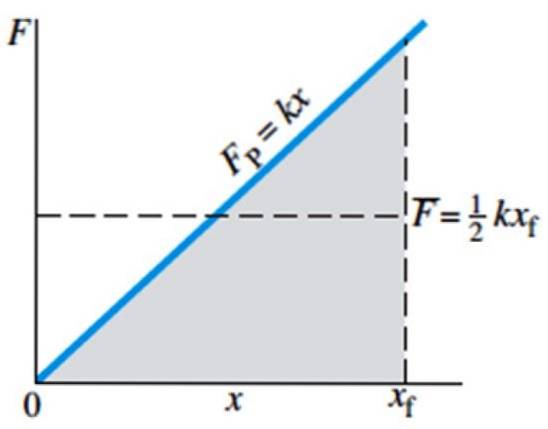
A força média é indicada no gráfico pela barra F e é igual a ½ kxF, onde xF é a posição final da mola.
Tanto a força exercida na mola quanto a força que ela exerce em um objeto amarrado a ela são forças variáveis. Quanto mais você deseja esticar ou comprimir a mola, mais força deve ser aplicada para alcançá-la..
Trabalho feito para esticar ou comprimir uma mola
Quando uma força deformadora é aplicada à mola, é feito um trabalho que é armazenado na mola e pode ser usado posteriormente..
Trabalho mecânico é definido como a área sob o gráfico da força F em função da posição x. Para calcular o trabalho W que uma força variável F (x) faz ao mover um objeto da posição x1 até a posição xdois devemos calcular a integral definida:
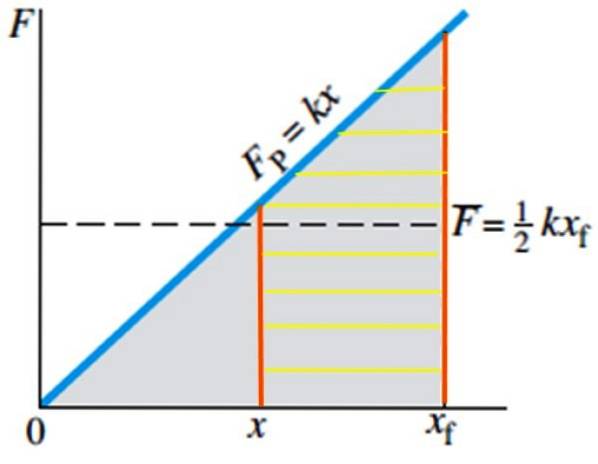
No caso do trabalho necessário para trazer uma mola de sua posição de equilíbrio para a posição xF É muito simples, pois a área a ser calculada é a do triângulo sombreado em cinza na figura 4, cuja fórmula é conhecida:
Área do triângulo = ½ base. altura
Portanto, o trabalho necessário é:
W = ½ xF . (kxF) = ½ k (xF)dois
E se você quiser calcular o trabalho necessário para trazer a mola da posição x para a posição xF, seria equivalente a calcular a área do trapézio hachurado na figura 5:
W = ½ k (xF)dois - ½ k xdois

Exemplos de molas
Dependendo da aplicação a que se destinam, as molas podem ser helicoidais, cilíndricas, cônicas, espirais, de seção transversal circular (as mais comuns), quadradas ou retangulares..
Uma classificação muito utilizada é de acordo com o tipo de esforço a que vão ser submetidos: são molas de torção, flexão, compressão e extensão. Os últimos são usados extensivamente e alguns funcionam igualmente para tensão e compressão..
Mola de compressão
Um exemplo de mola de compressão é aquela usada no brinquedo chamado pogo ou vara de salto. Essas molas armazenam muita energia potencial quando são comprimidas e a liberam aos poucos à medida que voltam à posição de equilíbrio. Desta forma, os rebotes não são muito abruptos.

Molas de extensão e torção
As molas do trampolim são do tipo de mola de extensão e são fabricadas com bobinas bem enroladas, com dois ganchos nas extremidades. Eles são capazes de reter muita energia potencial, que então liberam quando alguém sobe e começa a pular no tapete, que também tem sua própria resposta elástica, como todos os materiais..
As molas de torção são muito comuns, pois servem para fazer prendedores de roupa. Em vez de ganchos nas extremidades, eles se dobram em um ângulo para resistir às forças de torção.

Materiais para fazer molas
Os materiais mais adequados para fazer molas são aqueles com um resistência final (resistência final) alta, ou seja, suportam um grande esforço antes de quebrar. Também é desejável que o material tenha um alto limite de escoamento, para que não perca suas qualidades elásticas com pequenos esforços..
As molas reforçadas são feitas de ligas, incluindo aço de alto carbono, cobre, níquel e bronze.
Aplicações da Lei de Hooke
Como as molas têm a virtude de armazenar energia potencial quando esticadas ou comprimidas, elas são capazes de funcionar movendo coisas como mecanismos..
Desta forma, as molas têm uma infinidade de aplicações, desde pequenos objetos do dia-a-dia, passando por automóveis, até máquinas de todos os tipos. As molas são usadas para:
-Amortece vibrações.
-Fabrique mecanismos retráteis: canetas, prendedores de roupa, grampos de cabelo.
-Faça balanças de mola ou dinamômetros
E também fazem parte do mecanismo de:
-Relógios.
-Trampolins.
-Fechaduras.
-Brinquedos.
-Armas.
-Medidores de agulha, por exemplo, o galvanômetro, usados para medir correntes, tensões e resistências.
Exercícios resolvidos
- Exercício 1
Uma força de magnitude 5,0 N é aplicada a uma mola, fazendo com que um comprimento de 3,5 cm seja esticado de seu comprimento natural..
a) Quanto estica quando a força aplicada é de 7 N?
b) Encontre o trabalho realizado pela força aplicada para esticar a mola 3,5 cm de seu comprimento natural.
Solução para
Sabendo que a mola é esticada 3,5 cm aplicando 5,0 N, podemos calcular sua constante:
k = F / x = 5,0 N / 3,5 cm = 1,43 N / cm.
Quando uma força de 7 N é aplicada, o seguinte alongamento é obtido:
x = F / k = 7,0 N / 1,43 N / m = 4,9 cm
Solução b
O trabalho necessário para deformar uma mola é dado por:
W = ½ kxdois = 0,5 x 1,43 N / cm x (3,5 cm)dois = 8,76 N. cm = 8,76 N. 1 x 10 -dois m = 0,0876 J.
- Exercício 2
Uma mola de massa desprezível e 10 cm de comprimento está suspensa em um suporte. Se uma massa de 2 kg é pendurada nele, a mola é esticada para 15 cm. Calcular:
a) A constante da mola
b) O tamanho da mola quando uma massa de 3 kg é suspensa.
Solução para
O trecho da mola é x = 15 - 10 cm = 5 cm
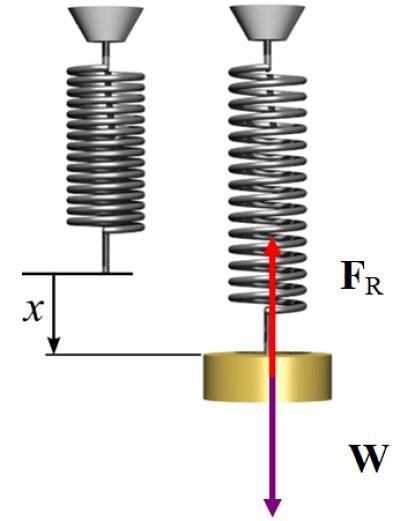
Como o sistema está em equilíbrio estático, a força exercida pela mola durante o alongamento é direcionada verticalmente para cima, para compensar o peso, que é direcionado para baixo, então:
FR = W → kx = mg
k = 2 x 9,8 N / 5 x 10 -dois m = 392 N / m
Solução b
Quando um peso de 3 kg é suspenso, a nova força é W = 3 x 9,8 N = 29,4 N
Nesse caso, o alongamento é:
x = mg / k = 29. 4 N / 392 N / m = 0,075 m = 7,5 cm
Referências
- Bauer, W. 2011. Physics for Engineering and Sciences. Volume 1. Mc Graw Hill.
- Blog de mecanismos criativos. Quatro tipos diferentes de molas. Recuperado de: creativemechanisms.com.
- Figueroa, D. (2005). Série: Física para Ciência e Engenharia. Volume 2. Dynamics. Editado por Douglas Figueroa (USB).
- Giancoli, D. 2006. Física: Princípios com Aplicações. 6º. Ed. Prentice Hall.
- .



Ainda sem comentários