
Unidades e fórmulas da lei de Ohm, cálculo, exemplos, exercícios
O Lei de Ohm, em sua forma macroscópica, indica que a tensão e a intensidade da corrente em um circuito são diretamente proporcionais, sendo a resistência a constante de proporcionalidade. Denotando essas três quantidades como V, I e R respectivamente, a lei de Ohm afirma que: V = I.R.
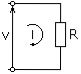
Da mesma forma, a lei de Ohm é generalizada para incluir elementos de circuito que não são puramente resistivos em circuitos de corrente alternada, desta forma assume a seguinte forma: V = I. Z.

Onde Z é a impedância, que também representa a oposição à passagem de corrente alternada por um elemento de circuito, por exemplo, um capacitor ou uma indutância.
Deve-se notar que nem todos os materiais e elementos do circuito estão de acordo com a lei de Ohm. Aqueles em que é válido são chamados de elementos ôhmico, e em que não é cumprido, eles são não ôhmico ou não linear.
Resistores elétricos comuns são do tipo ôhmico, mas diodos e transistores não, visto que a relação entre tensão e corrente não é linear neles..
A Lei de Ohm deve seu nome ao físico e matemático alemão nascido na Bavária George Simon Ohm (1789-1854), que passou sua carreira estudando o comportamento de circuitos elétricos. A unidade de resistência elétrica no Sistema Internacional SI foi nomeada em sua homenagem: o ohm, que também é expresso pela letra grega Ω.
Índice do artigo
- 1 Como é calculado?
- 1.1 A resistência de um condutor
- 2 exemplos
- 2.1 Experimente para verificar a lei de Ohm
- 2.2 Analogia hidráulica da lei de Ohm
- 3 exercícios
- 3.1 - Exercício 1
- 3.2 - Exercício 2
- 4 referências
Como é calculado?
Embora a forma macroscópica da lei de Ohm seja a mais conhecida, uma vez que liga quantidades que são facilmente mensuráveis em laboratório, o forma microscópica relaciona duas grandezas vetoriais importantes: o campo elétrico E e a densidade atual J:
J = σ.E
Onde σ é a condutividade elétrica do material, uma propriedade que indica como é fácil conduzir corrente. Por sua parte J é um vetor cuja magnitude é o quociente entre a intensidade da corrente I e a área da seção transversal A através da qual circula.
É lógico supor que existe uma conexão natural entre o campo elétrico dentro de um material e a corrente elétrica que circula por ele, de modo que quanto maior a corrente, mais corrente.
Mas a corrente não é um vetor, pois não tem direção no espaço. Em vez do vetor J é perpendicular -ou normal- à área da seção transversal do condutor e sua direção é a da corrente.
Desta forma da lei de Ohm chegamos à primeira equação, assumindo um condutor de comprimento ℓ e seção transversal A, e substituindo as magnitudes de J Y E para:
J = I / A
E = V / ℓ
J = σ.E → I / A = σ. (V / ℓ)
V = (ℓ / σ.A) .I
O inverso da condutividade é chamado resistividade e é denotado pela letra grega ρ:
1 / σ = ρ
Portanto:
V = (ρℓ / A) .I = R.I
A resistência de um condutor
Na equação V = (ρℓ / A) .I, a constante (ρℓ / A) é a resistência, portanto:
R = ρℓ / A
A resistência do condutor depende de três fatores:
-Sua resistividade ρ, típica do material com o qual é feito.
-O comprimento ℓ.
-A área A de sua seção transversal.
Quanto maior ℓ, maior a resistência, pois os portadores de corrente têm mais oportunidades de colidir com outras partículas dentro do condutor e perder energia. E, ao contrário, quanto maior A, mais fácil é para os portadores atuais se moverem de maneira ordenada através do material..
Por fim, na estrutura molecular de cada material reside a facilidade com que uma substância permite a passagem da corrente elétrica. Assim, por exemplo, metais como cobre, ouro, prata e platina, com baixa resistividade, são bons condutores, enquanto madeira, borracha e óleo não o são, por isso apresentam resistividade mais elevada..
Exemplos
Aqui estão dois exemplos ilustrativos da lei de Ohm.
Experimente verificar a lei de Ohm
Uma experiência simples ilustra a lei de Ohm, para isso é necessário um pedaço de material condutor, uma fonte de tensão variável e um multímetro.
Uma tensão V é estabelecida entre as extremidades do material condutor, que deve ser variada aos poucos. Com a fonte de alimentação variável podem ser ajustados os valores dessa tensão, que são medidos com o multímetro, bem como a corrente I que circula pelo condutor..
Os pares de valores V e I são registrados em uma tabela e um gráfico em papel milimetrado é construído com eles. Se a curva resultante for uma linha reta, o material é ôhmico, mas se for qualquer outra curva, o material é não ôhmico.
No primeiro caso, pode-se determinar a inclinação da linha, que equivale à resistência R do condutor ou seu inverso, a condutância.
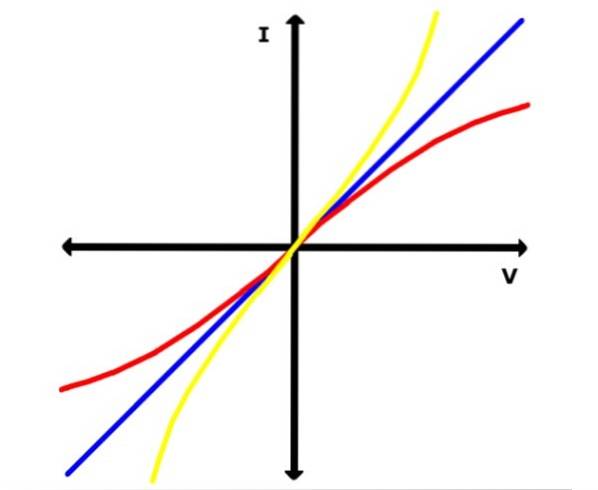
Na imagem abaixo, a linha azul representa um desses gráficos para um material ôhmico. Enquanto isso, as curvas amarela e vermelha são feitas de materiais não ôhmicos, como um semicondutor, por exemplo..
Analogia hidráulica da lei de Ohm
É interessante saber que a corrente elétrica na lei de Ohm se comporta de maneira semelhante à da água que flui por um cano. O físico inglês Oliver Lodge foi o primeiro a propor a simulação do comportamento da corrente utilizando elementos da hidráulica..
Por exemplo, os tubos representam os condutores, uma vez que a água circula por eles e a corrente, por eles. Quando há uma constrição na tubulação, a passagem de água é difícil, então isso seria equivalente a uma resistência elétrica.
A diferença de pressão nas duas extremidades do tubo permite que a água flua, o que proporciona uma diferença de altura ou uma bomba d'água, e da mesma forma, a diferença de potencial (a bateria) é o que mantém a carga em movimento., Equivalente ao fluxo ou volume de água por unidade de tempo.
Uma bomba de pistão desempenharia o papel de uma fonte de tensão alternada, mas a vantagem de colocar uma bomba d'água é que o circuito hidráulico seria fechado, assim como um circuito elétrico deve estar para que a corrente flua.

Resistores e interruptores
O equivalente a uma chave em um circuito, seria uma torneira. É interpretado desta forma: se o circuito está aberto (torneira fechada), a corrente, como a água, não pode fluir.
Por outro lado, com o interruptor fechado (torneira totalmente aberta) tanto a corrente quanto a água podem fluir sem problemas através do condutor ou tubo.
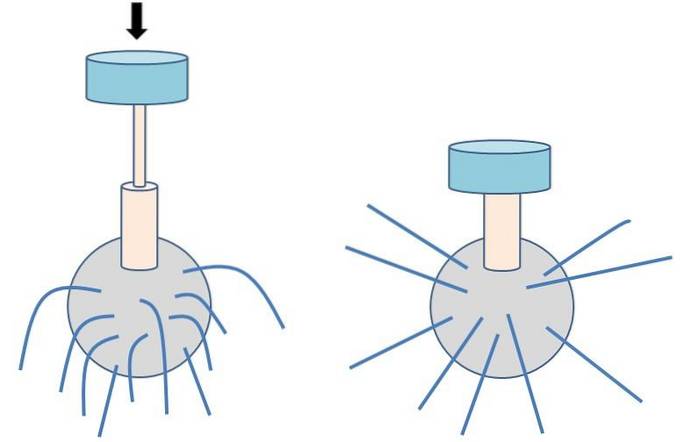
A torneira ou válvula também pode representar uma resistência: quando a torneira está totalmente aberta, equivale a ter uma resistência zero ou um curto-circuito. Se fechar completamente é como ter o circuito aberto, enquanto parcialmente fechado é como ter uma resistência de um determinado valor (ver figura 3).
Treinamento
- Exercício 1
Sabe-se que um ferro elétrico requer 2A a 120V para funcionar corretamente. Qual é a sua resistência?
Solução
Resolva a resistência da lei de Ohm:
R = V / I = 120 V / 2 A = 60 Ω
- Exercício 2
Um fio com diâmetro de 3 mm e comprimento de 150 m tem resistência elétrica de 3,00 Ω a 20 ° C. Encontre a resistividade do material.
Solução
A equação R = ρℓ / A é apropriado, portanto, a área da seção transversal precisa ser encontrada primeiro:
A = π(D / 2)dois = π (3 x 10-3 m / 2)dois = 4,5π x 10 -6 mdois
Finalmente, ao substituir você obtém:
ρ = A.R / ℓ = 4,5π x 10 -6 mdois x 3 Ω / 150 m = 2,83 x 10 -7 Ω.m
Referências
- Resnick, R. 1992. Physics. Terceira edição ampliada em espanhol. Volume 2. Compañía Editorial Continental S.A. por C.V.
- Sears, Zemansky. 2016. Física Universitária com Física Moderna. 14º. Ed. Volume 2. 817-820.
- Serway, R., Jewett, J. 2009. Física para Ciência e Engenharia com Física Moderna. 7ª Edição. Volume 2. Cengage Learning. 752-775.
- Tippens, P. 2011. Physics: Concepts and Applications. 7ª Edição. Colina Mcgraw.
- Sevilla University. Departamento de Física Aplicada III. Densidade e intensidade da corrente. Recuperado de: us.es.
- Walker, J. 2008. Physics. 4º Ed. Pearson. 725-728


Ainda sem comentários