
Explicação das leis de Gossen com exemplos
As Leis de Gossen, Criadas pelo economista alemão Hermann Gossen (1810-1858), são três leis da economia relevantes relacionadas à diminuição da utilidade marginal, custo marginal de aquisição e escassez..
Gossen foi o primeiro a explicar a lei da utilidade marginal decrescente, ou a primeira lei de Gossen, com base em observações gerais do comportamento humano. Esta lei afirma que o valor da mesma fruição diminui continuamente à medida que se avança sem interrupção nessa fruição, até que a satisfação seja alcançada..

A segunda lei, a lei da utilidade equi-marginal, explica o comportamento do consumidor quando ele tem recursos limitados, mas desejos ilimitados..
O problema fundamental em uma economia é que os desejos humanos são ilimitados, mas não existem recursos adequados para satisfazer todos os desejos humanos. Portanto, um indivíduo racional tenta otimizar os recursos escassos disponíveis para alcançar a satisfação máxima..
A terceira lei se refere ao valor econômico dos produtos, decorrente de uma escassez anterior.
Gossen se esforçou para encontrar cada uma dessas leis em todos os tipos de atividades econômicas.
Índice do artigo
- 1 Primeira Lei de Gossen
- 1.1 Exemplo
- 2 Segunda Lei de Gossen
- 2.1 Exemplo
- 3 Terceira Lei de Gossen
- 4 referências
Primeira Lei de Gossen
É conhecida como a lei da utilidade marginal decrescente. Afirma que quando um indivíduo consome mais de um produto, a utilidade total aumenta a uma taxa decrescente.
No entanto, após um certo estágio, a utilidade total também começa a diminuir e a utilidade marginal torna-se negativa. Isso significa que o indivíduo não precisa mais do produto..
Ou seja, o desejo de um indivíduo por um determinado produto fica saturado quando ele o consome cada vez mais..
Exemplo
Suponha que você esteja com fome e coma algumas laranjas. Comer a primeira laranja é muito útil. A utilidade marginal da segunda laranja é certamente menor do que a da primeira.
Da mesma forma, a utilidade marginal da terceira laranja é menor do que a da segunda, e assim por diante.
Após um determinado estágio, a utilidade marginal torna-se zero e, além desse estágio, torna-se negativa. Isso ocorre porque ele fica saciado à medida que mais e mais laranjas são consumidas..
Para entender melhor, você pode ver a tabela 1. Os números são hipotéticos e representam a utilidade marginal de consumir laranjas para uma pessoa.
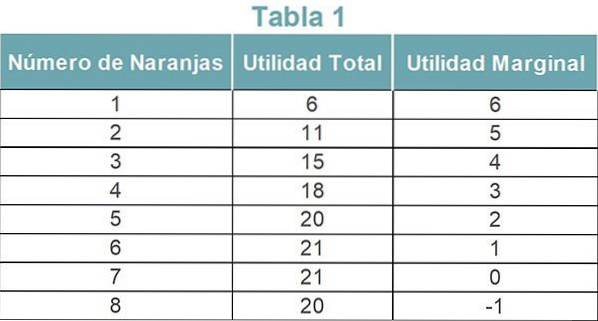
Lucro total
A utilidade total é obtida somando a utilidade marginal de cada unidade de laranja consumida. De acordo com a Tabela 1, a utilidade total das primeiras seis laranjas é 21 (21 = 6 + 5 + 4 + 3 + 2 + 1).
Utilidade marginal
A utilidade marginal da enésima unidade do produto é a diferença entre a utilidade total da enésima unidade e a utilidade total da (n-1) -ésima unidade do produto. UMn = UTn - UT (n-1) onde,
MUn = utilidade marginal da enésima unidade.
UTn = Lucro total da enésima unidade.
UT (n-1) = Lucro total da unidade (n-1) -ésima.
No exemplo da Tabela 1, a utilidade marginal da quarta laranja é CU4 = TU4-TU3 = 18-15 = 3.
A figura a seguir detalha as trajetórias das curvas de utilidade total e utilidade marginal.
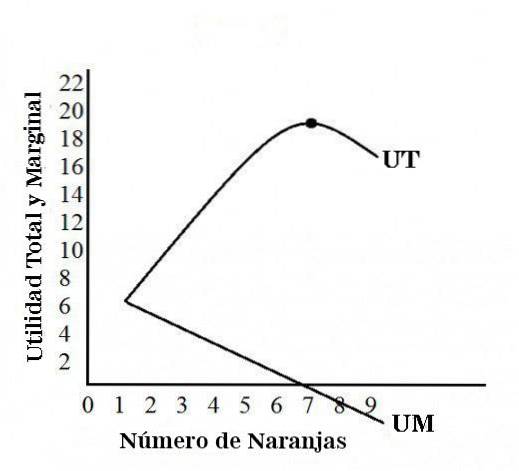
A curva de utilidade total aumenta inicialmente e, após um determinado estágio, começa a diminuir. É neste estágio que a curva de utilidade marginal entra na zona negativa..
Segunda lei de Gossen
A segunda lei diz que cada pessoa vai gastar seu dinheiro em produtos diferentes, de forma que a quantidade de todos os prazeres seja igual.
Desta forma, Gossen explicou que o máximo prazer seria alcançado a partir de um nível uniforme de satisfação. A segunda lei de Gossen é conhecida como a lei da utilidade equi-marginal.
Suponha que uma pessoa possua $ 200. A lei explica como a pessoa distribui os $ 200 entre seus diferentes desejos para maximizar sua satisfação..
O ponto em que a satisfação do consumidor é mais alta com os recursos fornecidos é conhecido como equilíbrio do consumidor..
Exemplo
Suponha que haja dois produtos X e Y. O recurso do consumidor é $ 8. O preço unitário do produto X é $ 1. O preço unitário do produto Y é $ 1.
O consumidor gasta seus $ 8 comprando o produto X. Como o preço unitário do produto X é $ 1, ele pode comprar 8 unidades.
A Tabela 2 mostra a utilidade marginal de cada unidade do produto X. Como a lei é baseada no conceito de utilidade marginal decrescente, ela diminui com cada unidade subsequente..
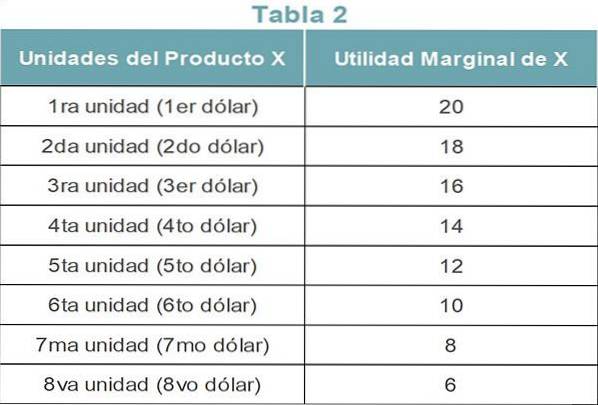
Agora considere que o consumidor gasta seus $ 8 comprando o produto Y. A Tabela 3 mostra a utilidade marginal de cada unidade do produto Y.
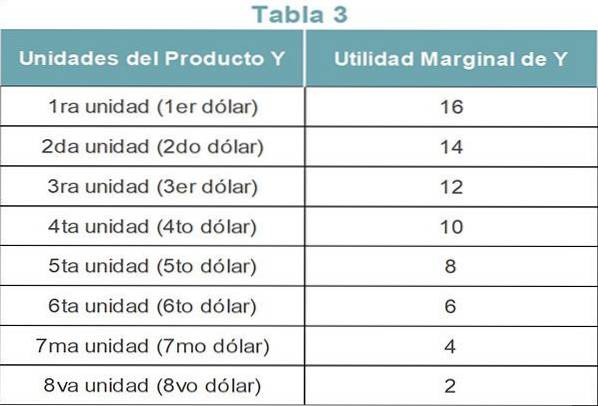
Se o consumidor planeja alocar seus $ 8 entre os produtos X e Y, a Tabela 4 mostra como o consumidor gasta sua renda com os dois produtos..
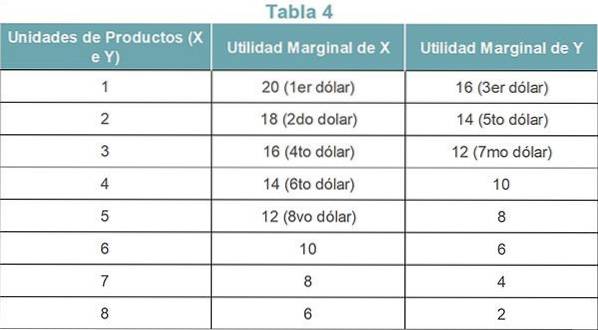
Aplicação da segunda lei
Como a primeira unidade do produto X dá o maior lucro (20), ela gasta o primeiro dólar em X. O segundo dólar também vai para o produto X, pois dá 18, o segundo maior.
Tanto a primeira unidade do produto Y quanto a terceira unidade do produto X oferecem a mesma quantidade de lucro. O consumidor prefere comprar o produto Y, porque já gastou dois dólares no produto X.
Da mesma forma, o quarto dólar é gasto em X, o quinto dólar em Y, o sexto dólar em X, o sétimo dólar em Y e o oitavo dólar em X.
Assim, o consumidor compra 5 unidades do produto X e 3 unidades do produto Y. Ou seja, 5 unidades do produto X e 3 unidades do produto Y o deixam com a melhor quantidade de utilidade total.
De acordo com a lei da utilidade eqüi-marginal, o consumidor está em equilíbrio neste ponto, com satisfação máxima. Para entender isso, a utilidade total dos produtos consumidos pode ser calculada.
Lucro total = UTx + UTy = (20 + 18 + 16 + 14 + 12) + (16 + 14 + 12) = 122. Qualquer outra combinação de produtos deixaria o cliente com um lucro total menor.
Terceira lei de Gossen
Essa lei indica que a escassez é uma pré-condição necessária para a existência de valor econômico. Ou seja, um produto tem valor apenas quando sua demanda excede seu fornecimento.
Usando a lógica de Gossen, uma vez que a utilidade marginal diminui com o consumo, um produto só pode ter uma utilidade marginal positiva ou "valor" se a oferta disponível for menor do que o necessário para gerar saciedade. Caso contrário, o desejo será saciado e, portanto, seu valor será zero.
Os argumentos de Gossen sobre o valor baseiam-se nas duas leis anteriores. Segundo ele, valor é um termo relativo. Depende da relação entre o objeto e o sujeito.
À medida que a quantidade aumenta, o valor de cada unidade adicionada diminui, até se tornar zero.
Referências
- Kirti Shailes (2018). Primeira e segunda lei de Gossen do prazer humano. Discussão de Economia. Retirado de: economicsdiscussion.net.
- Sundaram Ponnusamy (2014). A Lei da Utilidade Marginal Diminutiva ou Primeira Lei de Gossen. Owlcation. Retirado de: owlcation.com.
- Sundaram Ponnusamy (2016). A Lei da Utilidade Equi-Marginal ou Segunda Lei de Gossen. Owlcation. Retirado de: owlcation.com.
- Economics Concepts (2015). Lei da utilidade marginal decrescente. Retirado de: economicsconcepts.com.
- Wikipedia, a enciclopédia livre (2018). Leis de Gossen. Retirado de: en.wikipedia.org.



Ainda sem comentários