
Elementos de álgebra de blocos, exemplos, exercícios resolvidos
O álgebra de blocos refere-se ao conjunto de operações que são executadas por meio de blocos. Esses e alguns outros elementos servem para representar esquematicamente um sistema e visualizar facilmente sua resposta a uma determinada entrada..
Em geral, um sistema contém diversos elementos elétricos, eletrônicos e eletromecânicos, sendo que cada um deles, com sua respectiva função e posição no sistema, bem como a forma como se relacionam, é delineado através de blocos funcionais.
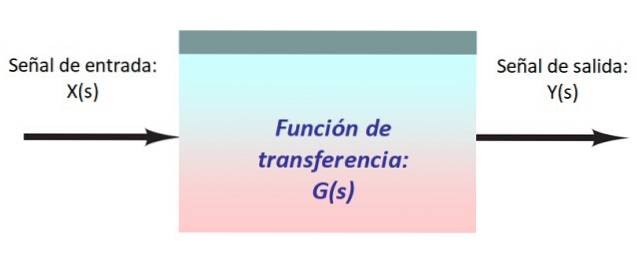
Na figura acima existe um sistema muito simples, constituído por um sinal de entrada X (s), que entra no bloco com a função de transferência G (s) que o modifica e produz a saída Y (s).
É conveniente representar os sinais e sua trajetória no sistema por meio de setas que entram e saem de cada bloco. Normalmente, o fluxo do sinal é direcionado da esquerda para a direita.
A vantagem desse tipo de esquema é o auxílio visual que ele fornece para a compreensão do sistema, embora não seja uma representação física do sistema. Na verdade, o diagrama de blocos não é único, pois dependendo do ponto de vista, vários diagramas do mesmo sistema podem até ser desenhados..
Também pode acontecer que um mesmo diagrama sirva a vários sistemas que não necessariamente se relacionam entre si, desde que descreva de forma adequada o seu comportamento. Existem diferentes sistemas cuja resposta é semelhante em muitos aspectos, por exemplo, um circuito LC (indutor-capacitor) e um sistema massa-mola..
Índice do artigo
- 1 O que é um diagrama de blocos?
- 2 elementos do diagrama de blocos
- 2.1 O sinal
- 2.2 O bloco
- 2.3 Ponto de Soma
- 2.4 Ponto de ramificação
- 3 exemplos de regras de álgebra de bloco
- 3.1 Blocos em cascata
- 3.2 Blocos em paralelo
- 3.3 Mova um somador para a esquerda
- 3.4 Mova um somador para a direita
- 3.5 Movendo um ponto de ramificação da esquerda para a direita
- 3.6 Mova um ponto de ramificação da direita para a esquerda
- 3.7 Sistema de feedback
- 3.8 Sistema com feedback e transdutor
- 4 exercícios resolvidos
- 4.1 Exercício 1
- 4.2 Exercício 2
- 5 referências
O que é um diagrama de blocos?
Os sistemas são geralmente mais complicados do que o da Figura 1, mas a álgebra de blocos fornece uma série de regras simples para manipular o esquema do sistema e reduzi-lo à sua versão mais simples..
Conforme explicado no início, o diagrama usa blocos, setas e círculos para estabelecer a relação entre cada componente do sistema e o fluxo de sinais que passam por ele..
A álgebra de blocos permite que você compare dois ou mais sinais adicionando, subtraindo e multiplicando-os, bem como analisando a contribuição que cada componente faz para o sistema.
Graças a isso, é possível reduzir todo o sistema a um único sinal de entrada, uma única função de transferência que descreve totalmente a ação do sistema e a saída correspondente..
Elementos do diagrama de blocos
Os elementos do diagrama de blocos são os seguintes:
O sinal
Os sinais são de natureza muito variada, por exemplo, é comum que seja uma corrente elétrica ou uma voltagem, mas pode ser luz, som e muito mais. O importante é que contenha informações sobre um determinado sistema.
O sinal é denotado por uma letra maiúscula se for uma função da variável s da transformada de Laplace: X (s) (ver figura 1) ou com letras minúsculas se for função do tempo t, como x (t).
No diagrama de blocos, o sinal de entrada é representado por uma seta direcionada para o bloco, enquanto o sinal de saída, denotado como Y (s) ou y (t), é indicado por uma seta saindo.
Ambos os sinais de entrada e saída são únicos e a direção do fluxo de informações é determinada pela direção da seta. E a álgebra é a mesma para qualquer uma das duas variáveis.
O bloco
O bloco é representado por um quadrado ou retângulo (ver figura 1) e pode ser usado para realizar operações ou implementar a função de transferência, que geralmente é denotada pela letra maiúscula G. Esta função é um modelo matemático que descreve a resposta oferecido pelo sistema para um sinal de entrada.
A função de transferência pode ser expressa em termos de tempo t como G (t) ou a variável s como G (s).
Quando o sinal de entrada X (s) atinge o bloco, ele é multiplicado pela função de transferência e transformado no sinal de saída Y (s). Matematicamente, é expresso assim:
Y (s) = X (s) .G (s)
De forma equivalente, a função de transferência é a razão entre a transformada de Laplace do sinal de saída e a transformada de Laplace do sinal de entrada, desde que as condições iniciais do sistema sejam nulas:
G (s) = Y (s) / X (s)
Ponto de soma
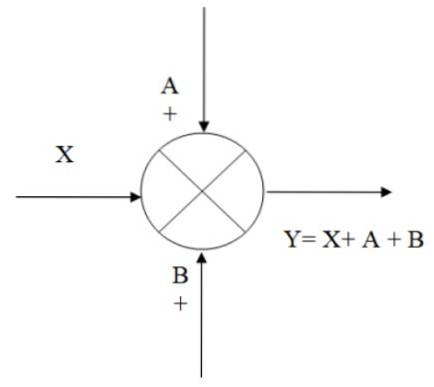
O ponto de adição, ou somador, é simbolizado por um círculo com uma cruz dentro. É usado para combinar, por meio de adição e subtração, dois ou mais sinais. No final da seta que simboliza o sinal, um sinal + é colocado diretamente se o referido sinal for adicionado ou um sinal - se for subtraído..
Na figura a seguir há um exemplo de como funciona o somador: temos o sinal de entrada X, ao qual se somam os sinais A e B, obtendo-se como resultado a saída Y, que é algebricamente equivalente a:
Y = X + A + B
Ponto de ramificação
Também é chamado ponto de bifurcação. Nele, o sinal que sai de um bloco é distribuído para outros blocos ou para um somador. É representado por um ponto colocado na seta de sinal e sai outra seta que redireciona o sinal para outra parte.
Exemplos de regras de álgebra de blocos
Conforme explicado anteriormente, a ideia é expressar o sistema usando o diagrama de blocos e reduzi-lo para encontrar a função de transferência que o descreve. A seguir estão as regras de álgebra de blocos para simplificar os diagramas:
Blocos em cascata
Quando você tem um sinal que passa sucessivamente pelos blocos G1, Gdois, G3..., é reduzido a um único bloco cuja função de transferência é o produto de G1, Gdois, G3...
No exemplo a seguir, o sinal X (s) entra no primeiro bloco e sua saída é:
Y1(s) = X (s) .G1(s)

Vire Y1(s) entrar no bloco Gdois(s), cuja saída é:
Ydois(s) = X (s) .G1(s). Gdois(s)
O procedimento é válido para n blocos em cascata:
Yn (s) = X (s). G1(s) .Gdois(s) ... Gn(s)
Blocos paralelos
No diagrama à esquerda, o sinal X (s) se ramifica para entrar nos blocos G1(s) e Gdois(s):
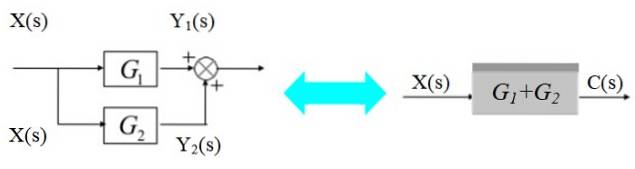
Os respectivos sinais de saída são:
Y1(s) = X (s) .G1(s)
Ydois(s) = X (s) .Gdois(s)
Esses sinais são somados para obter:
C (s) = Y1(s) + Ydois(s) = X (s). [G1(s) + Gdois(s)]
Conforme mostrado no diagrama à direita.
Mova um somador para a esquerda
Um somador pode ser deslocado para a esquerda do bloco da seguinte forma:
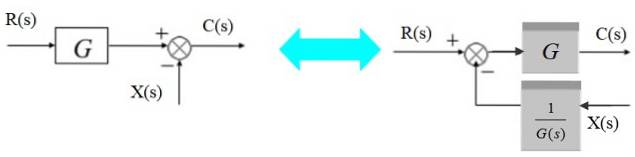
À esquerda, o sinal de saída é:
C (s) = R (s). G (s) - X (s)
Equivalentemente à direita:
C (s) = [R (s) - X (s) / G (s)]. G (s)
Mova um somador para a direita
O somador pode ser movido para a direita do bloco assim:
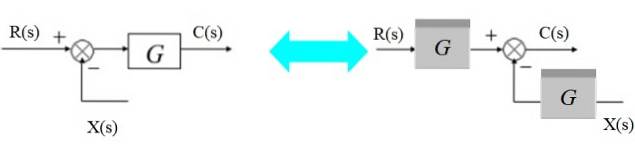
À esquerda temos: [R (s) - X (s)]. G (s) = C (s)
E à direita:
R (s). G (s) - X (s). G (s) = C (s)
Mova um ponto de ramificação da esquerda para a direita
Para mover o ponto de ramificação da esquerda para a direita do bloco, basta observar que a saída C (s) para a direita é o produto X (s) .G (s). Já que você deseja convertê-lo para X (s) novamente, multiplique pelo inverso de G (s).
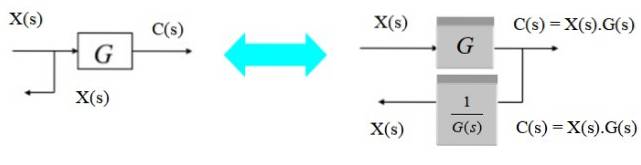
Mova um ponto de ramificação da direita para a esquerda
Alternativamente, o ponto de ramificação pode ser deslocado da direita para a esquerda da seguinte forma:

Como na saída do ramal queremos obter C (s), basta inserir um novo bloco G (s) em um ponto do ramal à esquerda do bloco original.
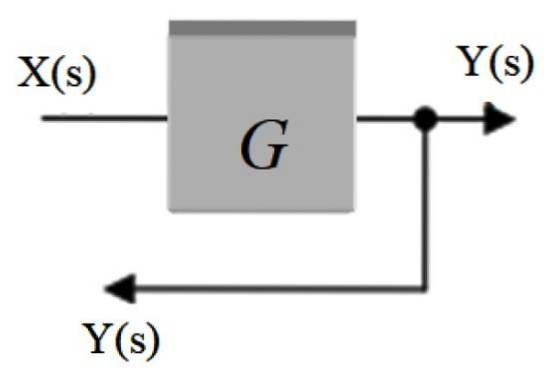
Sistema de feedback
No sistema a seguir, o sinal de saída C (s) é realimentado através do somador à esquerda:
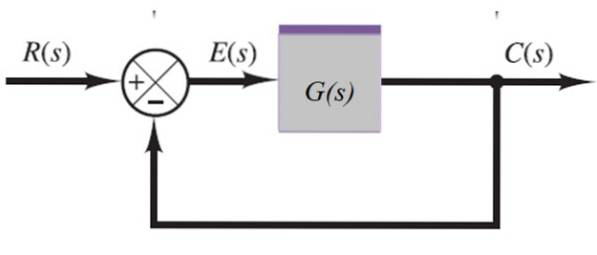
C (s) = E (s) .G (s)
Mas:
E (s) = R (s) -C (s)
Substituindo essa expressão na equação anterior, ela permanece: C (s) = [R (s) -C (s)]. G (s), a partir do qual C (s) pode ser resolvido:
C (s) + C (s) .G (s) = R (s) .G (s) → C (s). [1 + G (s)] = R (s) .G (s)
C (s) = R (s). G (s) / [1 + G (s)]
Ou alternativamente:
C (s) / R (s) = G (s) / [1 + G (s)]
Na forma gráfica, depois de simplificado permanece:
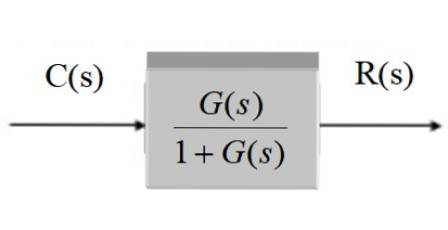
Sistema com feedback e transdutor
O transdutor consiste na função de transferência H (s):
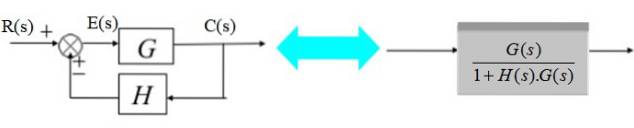
No diagrama à direita, o sinal de saída C (s) é:
C (s) = E (s). G (s) com E (s) = R (s) - C (s). H (s)
Então:
C (s) = [R (s) - C (s). H (s)]. G (s)
C (s) [1+ H (s) .G (s)] = R (s) .G (s)
Portanto, C (s) pode ser resolvido por:
C (s) = G (s) .R (s) / [1+ H (s) .G (s)]
E a função de transferência será:
G (s) / [1+ H (s) .G (s)]
Conforme mostrado no diagrama simplificado à direita.
Exercícios resolvidos
Exercício 1
Encontre a função de transferência do seguinte sistema:
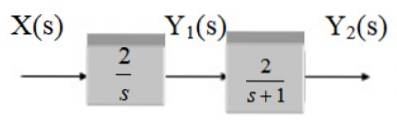
Solução
Trata dois blocos em cascata, pois a função de transferência é o produto das funções G1 e Gdois.
Se tem que:
G1 = 2 / s
Gdois = 2 / (s + 1)
Portanto, a função de transferência procurada é:
G (s) = 4 / [s (s + 1)]
Exercício 2
Reduza o seguinte sistema:
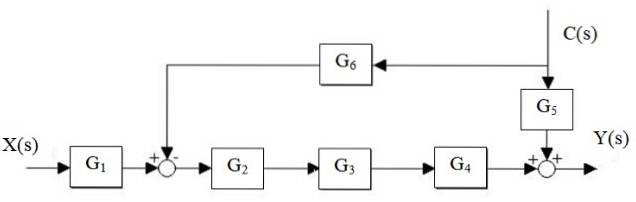
Solução
Primeiro, a cascata G é reduzidadois, G3 e G4, e o G paralelo é separado5 e G6:

Em seguida, o somador à esquerda do bloco Gdois ⋅G3 ⋅ G4 move-se para a direita:
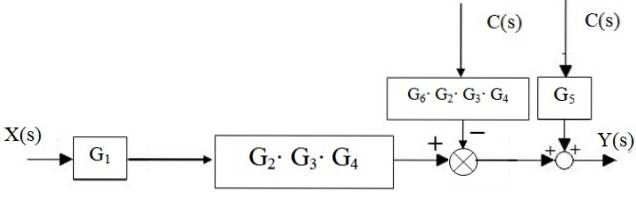
Os somadores à direita são reduzidos a apenas um, assim como os blocos em cascata:
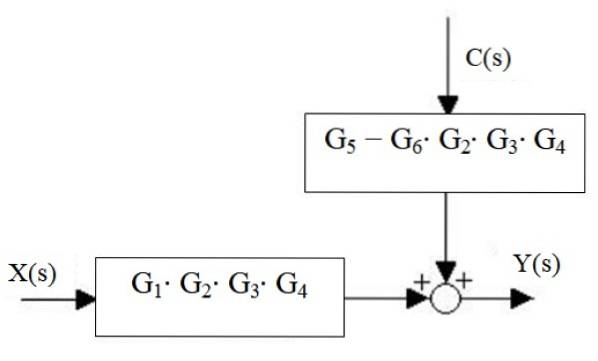
Finalmente, a saída do sistema é:
Y (s) = X (s) ⋅G1⋅ Gdois ⋅G3 ⋅ G4 + C (s) ⋅ [G5 - G6 ⋅ Gdois ⋅G3 ⋅ G4]
Referências
- Alaydi, J. Control system block diagram. Recuperado de: site.iugaza.edu.ps.
- Bolton, W. 2006. Engenharia de controle. 2ª Edição. Alfa Ômega.
- Cwalinsky, J. Introduction to system block algebra. Recuperado de: cedengineering.com.
- Dademuchconnection. Diagrama de blocos. Recuperado de: dademuch.com.
- Ogata, K. 2010. Modern control engineering. 5 ª. Edição. Pearson.



Ainda sem comentários