
Características da linha perpendicular, exemplos, exercícios
UMA linha perpendicular É aquele que forma um ângulo de 90º em relação a outra linha, curva ou superfície. Observe que quando duas linhas são perpendiculares e estão no mesmo plano, quando se cruzam formam quatro ângulos idênticos, cada um de 90º.
Se um dos ângulos não for 90º, as linhas são ditas oblíquas. Linhas perpendiculares são comuns em design, arquitetura e construção, por exemplo, a rede de tubos na imagem a seguir.

A orientação das linhas perpendiculares pode ser diversa, como as mostradas abaixo:
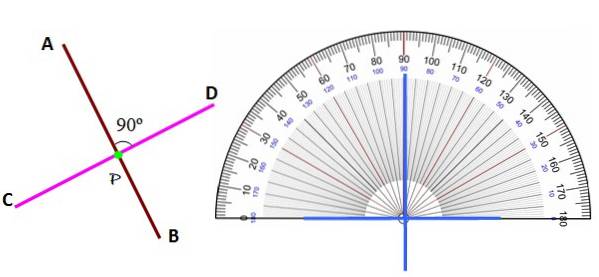
Independentemente da posição, as linhas perpendiculares entre si são reconhecidas identificando o ângulo entre elas como 90º, com a ajuda do transferidor.
Observe que, ao contrário das linhas paralelas no plano, que nunca se cruzam, as linhas perpendiculares sempre o fazem em um ponto P, chamado pé de uma das linhas sobre a outra. Portanto, duas linhas perpendiculares também são mata-borrões.
Qualquer linha tem infinitas perpendiculares a ela, pois apenas movendo o segmento AB para a esquerda ou direita sobre o segmento CD, teremos novas perpendiculares com outro pé.
No entanto, a perpendicular que passa apenas pelo ponto médio de um segmento é chamada bissetriz do referido segmento.
Índice do artigo
- 1 Exemplos de linhas perpendiculares
- 1.1 Mais exemplos de linhas perpendiculares
- 2 exercícios
- 2.1 - Exercício 1
- 2.2 - Exercício 2
- 3 referências
Exemplos de linhas perpendiculares
Linhas perpendiculares são comuns na paisagem urbana. Na imagem a seguir (figura 3), apenas algumas das muitas linhas perpendiculares que podem ser vistas na fachada simples deste edifício e seus elementos como portas, dutos, degraus e outros foram destacados:

O bom é que três linhas perpendiculares entre si nos ajudam a estabelecer a localização de pontos e objetos no espaço. Eles são os eixos coordenados identificados como Eixo X, Eixo y Y eixo z, claramente visível no canto de uma sala retangular como a que está abaixo:
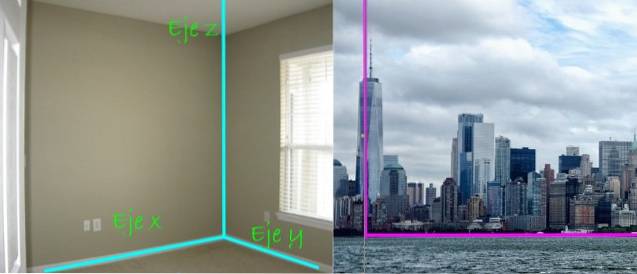
Na vista panorâmica da cidade, à direita, também se nota a perpendicularidade entre o arranha-céu e o solo. O primeiro, diríamos, é encontrado ao longo do eixo z, enquanto o solo é um plano, que neste caso é o plano xy.
Se o solo constitui o plano xy, o arranha-céu também é perpendicular a qualquer avenida ou rua, o que garante sua estabilidade, já que uma estrutura inclinada é instável.
E nas ruas, onde quer que haja esquinas retangulares, existem linhas perpendiculares. Muitas avenidas e ruas têm traçado perpendicular, desde que o terreno e as características geográficas o permitam..
Para expressar brevemente a perpendicularidade entre linhas, segmentos ou vetores, o símbolo ⊥ é usado. Por exemplo, se a linha L1 é perpendicular à linha Ldois, nós escrevemos:
eu1 ⊥ Ldois
Mais exemplos de linhas perpendiculares
- No desenho as linhas perpendiculares estão muito presentes, já que muitos objetos comuns são baseados em quadrados e retângulos. Esses quadriláteros são caracterizados por apresentarem ângulos internos de 90º, pois seus lados são paralelos dois a dois:
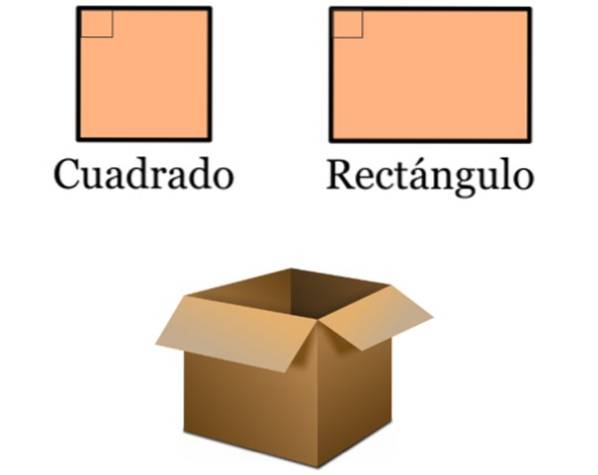
- Os campos nos quais são praticados diversos esportes são demarcados por numerosos quadrados e retângulos. Estes, por sua vez, contêm linhas perpendiculares.
- Dois dos segmentos que formam um triângulo retângulo são perpendiculares entre si. Estes são chamados pernas, enquanto a linha restante é chamada hipotenusa.
- As linhas do vetor de campo elétrico são perpendiculares à superfície de um condutor em equilíbrio eletrostático.
- Para um condutor carregado, as linhas e superfícies equipotenciais são sempre perpendiculares às do campo elétrico.
- Em sistemas de tubulação ou conduíte usados para transportar diferentes tipos de fluidos, como o gás mostrado na Figura 1, cotovelos em ângulo reto são comuns. Portanto, formam linhas perpendiculares, como é o caso de uma sala de caldeiras:

Treinamento
- Exercício 1
Desenhe duas linhas perpendiculares usando uma régua e compasso.
Solução
É muito simples de fazer, seguindo estas etapas:
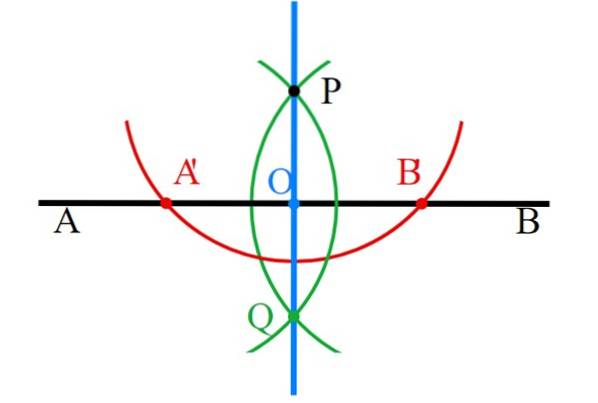
-A primeira linha é desenhada, chamada AB (preta).
-Acima (ou abaixo se preferir) marque o ponto P P, através do qual a perpendicular passará. Se P está logo acima (ou abaixo) do meio de AB, essa perpendicular é a bissetriz do segmento AB.
-Com a bússola centrada em P, desenhe um círculo que corta AB em dois pontos, chamados A 'e B' (vermelho).
-A bússola é aberta em A'P, é centralizada em A 'e um círculo é desenhado que passa por P (verde).
-Repita o passo anterior, mas agora abrindo a medida do comprimento do segmento B'P (verde). Ambos os arcos de circunferência se cruzam no ponto Q abaixo de P e, claro, no último.
-Os pontos P e Q são unidos com a régua e a linha perpendicular (azul) está pronta.
-Por fim, todas as construções auxiliares devem ser cuidadosamente apagadas, deixando apenas as perpendiculares..
- Exercício 2
Duas linhas L1 e eudois são perpendiculares se suas respectivas encostas m1 e mdois conhecer este relacionamento:
m1 = -1 / mdois
Dada a linha y = 5x - 2, encontre uma linha perpendicular a ela e que passe pelo ponto (-1, 3).
Solução
-Primeiro, encontre a inclinação da reta perpendicular m⊥, conforme indicado na declaração. A inclinação da linha original é m = 5, o coeficiente que acompanha “x”. Então:
m⊥= -1/5
-Em seguida, a equação da linha perpendicular é construída e⊥, substituindo o valor encontrado anteriormente:
Y⊥= -1 / 5x + b
-A seguir, o valor de b é determinado, com a ajuda do ponto dado pela afirmação, (-1,3), uma vez que a reta perpendicular deve passar por ele:
y = 3
x = -1
Substituindo:
3 = -1/5 (-1) + b
Resolva o valor de b:
b = 3- (1/5) = 14/5
-Finalmente, a equação definitiva é construída:
Y⊥= -1 / 5x + 14/5
Referências
- Baldor, A. 2004. Geometria plana e espacial. Publicações Culturais.
- Clemens, S. 2001. Geometria com aplicações e resolução de problemas. Addison wesley.
- Matemática é Fun. Linhas perpendiculares. Recuperado de: mathisfun.com.
- Monterey Institute. Linhas perpendiculares. Recuperado de: montereyinstitute.org.
- Wikipedia. Linhas perpendiculares. Recuperado de: es.wikipedia.org.



Ainda sem comentários