UMA magnitude do vetor é qualquer expressão representada por um vetor que possui valor numérico (módulo), direção, direção e ponto de aplicação. Alguns exemplos de quantidades vetoriais são deslocamento, velocidade, força e o campo elétrico.
A representação gráfica de uma grandeza vetorial consiste em uma seta cuja ponta indica sua direção e direção, seu comprimento é o módulo e o ponto de partida é a origem ou ponto de aplicação..
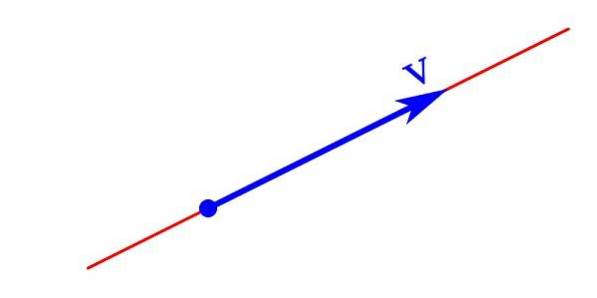
A quantidade vetorial é representada analiticamente por uma letra com uma seta no topo apontando para a direita em uma direção horizontal. Também pode ser representado por uma carta escrita em negrito V cujo módulo ǀVǀ está escrito em itálico V.
Uma das aplicações do conceito de magnitude vetorial está no projeto de rodovias e estradas, especificamente no projeto de suas curvaturas. Outra aplicação é o cálculo do deslocamento entre dois locais ou a mudança de velocidade de um veículo.
Índice do artigo
Uma quantidade vetorial é qualquer entidade representada por um segmento de reta, orientado no espaço, que possui as características de um vetor. Essas características são:
Módulo: É o valor numérico que indica o tamanho ou intensidade da magnitude do vetor.
Direção: É a orientação do segmento de linha no espaço que o contém. O vetor pode ter direção horizontal, vertical ou inclinada; norte, sul, leste ou oeste; nordeste, sudeste, sudoeste ou noroeste.
Senso: Indicado pela ponta de seta no final do vetor.
Ponto de aplicação: É a origem ou ponto de atuação inicial do vetor.
Os vetores são classificados como colineares, paralelos, perpendiculares, concorrentes, coplanares, livres, deslizantes, opostos, lentes de equipe, fixos e unitários..
Colinear: Eles pertencem ou agem na mesma linha reta, eles também são chamados linearmente dependente e pode ser vertical, horizontal e inclinado.
Paralelo: Eles têm a mesma direção ou inclinação.
Perpendicular: dois vetores são perpendiculares entre si quando o ângulo entre eles é de 90 °.
Concorrente: São vetores que, ao deslizarem ao longo de sua linha de ação, coincidem no mesmo ponto no espaço.
Coplanários: Eles atuam em um avião, por exemplo, o avião xy.
Livre: Eles se movem em qualquer ponto do espaço, mantendo seu módulo, direção e sentido.
Sliders: Eles se movem ao longo da linha de ação determinada por sua direção.
Opostos: Eles têm o mesmo módulo e direção, e a direção oposta.
Teamlenses: Eles têm o mesmo módulo, direção e sentido.
Fixo: Eles têm o ponto de aplicação invariável.
Unitário: Vetores cujo módulo é a unidade.
Uma quantidade vetorial no espaço tridimensional é representada em um sistema de três eixos mutuamente perpendiculares (X e Z) chamado triédrico ortogonal.
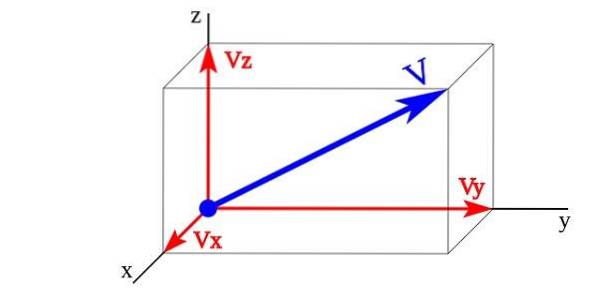
Na imagem os vetores Vx, Vy, Vz são os componentes vetoriais do vetor V cujos vetores unitários são x,Y,z. A magnitude do vetor V é representado pela soma de seus componentes vetoriais.
V = Vx + Vy + Vz
A resultante de várias quantidades vetoriais é a soma vetorial de todos os vetores e substitui esses vetores em um sistema.
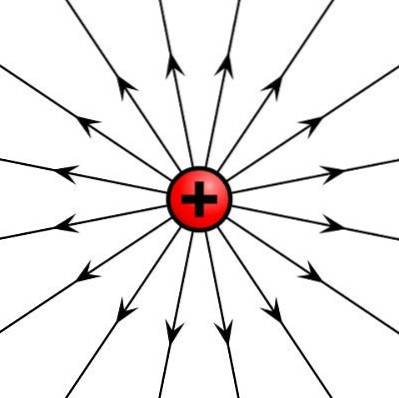
O campo vetorial é a região do espaço em que a magnitude do vetor corresponde a cada um de seus pontos. Se a magnitude que se manifesta é uma força agindo sobre um corpo ou sistema físico, então o campo vetorial é um campo de forças.
O campo vetorial é representado graficamente por linhas de campo que são linhas tangentes da magnitude do vetor em todos os pontos da região. Alguns exemplos de campos vetoriais são o campo elétrico criado por uma carga elétrica pontual no espaço e o campo de velocidade de um fluido.
Adicionando vetores: É o resultado de dois ou mais vetores. Se tivermos dois vetores OU Y P a soma é OU + P = Q. O vetor Q é o vetor resultante que é obtido graficamente pela tradução da origem do vetor PARA ao final do vetor B.
Subtração vetorial: A subtração de dois vetores O e P isso é OU - P = Q. O vetor Q é obtido adicionando ao vetor OU é o contrário -P. O método gráfico é o mesmo da soma com a diferença que o vetor oposto é transferido para o extremo.
Produto escalar: O produto de uma quantidade escalar para por uma magnitude de vetor P é um vetor mP que tem a mesma direção do vetor P. Se a magnitude escalar é zero, o produto escalar é um vetor zero.
A posição de um objeto ou partícula em relação a um sistema de referência é um vetor que é dado por suas coordenadas retangulares X e Z, e é representado por seus componentes vetoriais XI, eĵ, zk. Vetores eu, ĵ, k eles são vetores unitários.
Uma partícula em um ponto (X e Z) tem um vetor de posição r = XI + eĵ + zk. O valor numérico do vetor de posição é r= √ (xdois + Ydois + zdois) A mudança na posição da partícula de uma posição para outra em relação a um referencial é o vetor Deslocamento Δr e é calculado com a seguinte expressão vetorial:
Δr = rdois - r1
Aceleração média (param) é definido como a mudança na velocidade v em um intervalo de tempo Δt e a expressão para calcular é param= Δv / Δt, sendo Δv o vetor de mudança de velocidade.
Aceleração instantânea (para) é o limite da aceleração média param quando Δt torna-se tão pequeno que tende a zero. A aceleração instantânea é expressa em função de seus componentes vetoriais
para =paraxeu +paraY ĵ+ parazk
A força de atração gravitacional exercida por uma massa M, localizado na origem, em outra massa m em um ponto no espaço x, Y, z é um campo vetorial denominado campo de força gravitacional. Essa força é dada pela expressão:
F= (- mMG /r)ȓ
r = XI + eĵ + zk
F = é a magnitude física da força gravitacional
G = é a constante de gravitação universal
ȓ = é o vetor posição da massa m
Ainda sem comentários