
Características, postulados, limitações do modelo atômico de Bohr

O Modelo atômico de Bohr é a concepção da estrutura do átomo do físico dinamarquês Niels Bohr (1885-1962), publicada em 1913. No átomo de Bohr, os elétrons ao redor do núcleo ocupam apenas algumas órbitas permitidas, graças a uma restrição chamada quantização.
Para Bohr, a imagem do átomo como um sistema solar em miniatura, com elétrons orbitando ao redor do núcleo, não era totalmente consistente com o fato de que cargas elétricas, quando aceleradas, irradiam energia..
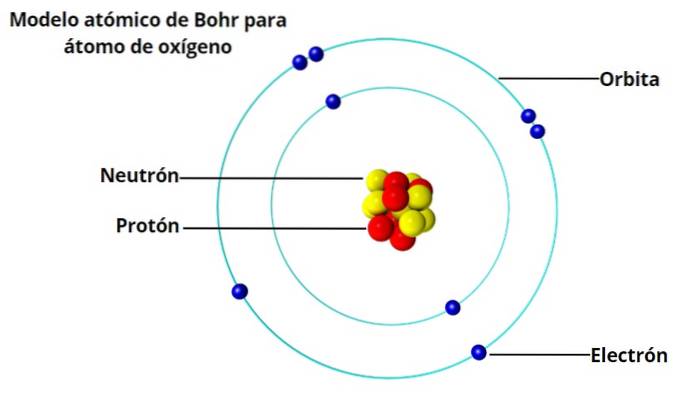
Esse átomo não seria estável, porque mais cedo ou mais tarde acabaria entrando em colapso porque os elétrons espiralariam em direção ao núcleo. E então, os padrões de luz característicos que o hidrogênio e outros gases emitem quando aquecidos já eram conhecidos há 50 anos..
O padrão ou espectro consiste em uma série de linhas brilhantes de certos comprimentos de onda muito específicos. E o átomo de hidrogênio não entra em colapso por emitir luz.
Para explicar por que o átomo é estável apesar de ser capaz de irradiar energia eletromagnética, Bohr propôs que o momento angular só poderia adotar certos valores e, portanto, também a energia. Isso é o que significa quantização.
Aceitando que a energia foi quantizada, o elétron teria a estabilidade necessária para não correr em direção ao núcleo destruindo o átomo..
E o átomo apenas irradia energia luminosa quando o elétron faz a transição de uma órbita para outra, sempre em quantidades discretas. Desta forma, a presença de padrões de emissão no hidrogênio é explicada..
Bohr então compôs uma visão do átomo integrando conceitos familiares da mecânica clássica com os recém-descobertos, como a constante de Planck, o fóton, o elétron, o núcleo atômico (Rutherford foi o mentor de Bohr) e os espectros de problema mencionados acima..
Índice do artigo
- 1 Principais características do modelo Bohr
- 1.1 Cálculo do raio da órbita do elétron
- 2 postulados do modelo atômico de Bohr
- 2.1 Elétrons descrevem caminhos circulares
- 2.2 O momento angular é quantizado
- 2.3 Elétrons emitem ou absorvem fótons ao passar de um estado de energia para outro
- 3 limitações
- 4 artigos de interesse
- 5 referências
Principais características do modelo Bohr
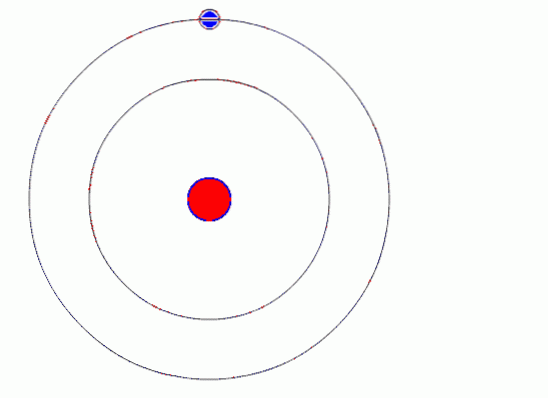
O modelo atômico de Bohr assume que o elétron se move em uma órbita circular ao redor do núcleo pela ação da força de atração eletrostática de Coulomb e propõe que o momento angular do elétron é quantizado.
Vamos ver como integrar os dois conceitos de forma matemática:
Seja L a magnitude do momento angular, m a massa do elétron, v a velocidade do elétron er o raio da órbita. Para calcular L, temos:
L = m⋅r⋅v
Bohr propôs que L era igual a múltiplos inteiros da constante h / 2π, onde h é o Constante de Planck, introduzida há pouco pelo físico Max Planck (1858-1947) ao resolver o problema da energia emitida por um corpo negro, objeto teórico que absorve toda a luz incidente.
Seu valor é h = 6,626 × 10-34 J ・ s, enquanto a h / 2π é denotado como ħ, o que é lido "Barra H".
Portanto, o momento angular L permanece:
m⋅r⋅v = nħ, com n = 1,2, 3 ...
E a partir desta condição são deduzidos os raios das órbitas permitidas para o elétron, como veremos a seguir..
Cálculo do raio da órbita do elétron
A seguir, assumiremos o mais simples dos átomos: o hidrogênio, que consiste em um único próton e um elétron, ambos com carga de magnitude e.
A força centrípeta que mantém o elétron em sua órbita circular é fornecida pela atração eletrostática, cuja magnitude F é:
F = kedois/ rdois
Onde k é a constante eletrostática da lei de Coulomb er a distância elétron-próton. Sabendo que em um movimento circular, a aceleração centrípeta emc é dado pela razão entre o quadrado da velocidade e a distância r:
parac = vdois / r
Pela segunda lei de Newton, a força resultante é o produto da massa me da aceleração:
mvdois/ r = kedois/ rdois
Simplificando o raio r, obtemos:
m⋅vdoisr = kedois
Combinando esta expressão com a do momento angular, temos um sistema de equações, dado por:
1) mvdoisr = kedois
2) r = n ħ/ mv
A ideia é resolver o sistema e determinar r, o raio da órbita permitida. Um pouco de álgebra elementar leva à resposta:
r = (nħ)dois / k⋅m⋅edois
Com n = 1, 2, 3, 4, 5 ...
Para n = 1, temos o menor dos raios, chamado Raio de Bohr paraou com um valor de 0,529 × 10-10 m. Os raios das outras órbitas são expressos em termos de paraou.
Desta forma, Bohr introduz o número quântico principal n, observando que os raios permitidos são uma função da constante de Planck, da constante eletrostática e da massa e carga do elétron.
Postulados do modelo atômico de Bohr

Bohr combina habilmente a mecânica newtoniana com novas descobertas que ocorreram continuamente durante a segunda metade do século XIX e o início do século XX. Entre eles o revolucionário conceito de "quantum", do qual o próprio Planck afirmava não estar muito convencido..
Por meio de sua teoria, Bohr conseguiu explicar satisfatoriamente as séries do espectro do hidrogênio e prever as emissões de energia na faixa do ultravioleta e infravermelho, que ainda não haviam sido observadas..
Podemos resumir seus postulados da seguinte forma:
Elétrons descrevem caminhos circulares
O elétron gira em torno do núcleo em uma órbita circular estável, com movimento circular uniforme. O movimento se deve à atração eletrostática que o núcleo exerce sobre ele.
O momento angular é quantizado
O momento angular do elétron é quantizado de acordo com a expressão:
L = mvr = nħ
Onde n é um inteiro: n = 1, 2, 3, 4 ..., o que leva ao fato de que o elétron só pode estar em certas órbitas definidas, cujos raios são:
r = (n ħ)dois / k m edois
Os elétrons emitem ou absorvem fótons ao passar de um estado de energia para outro
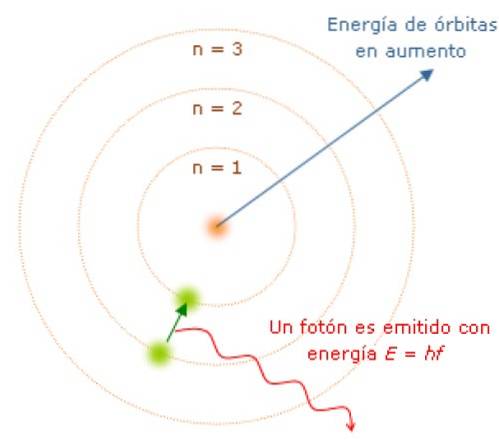
Uma vez que o momento angular é quantizado, também o é a energia E. Pode-se mostrar que E é dado por:


O elétron volt, ou eV, é outra unidade de energia, amplamente utilizada na física atômica. O sinal negativo na energia garante a estabilidade da órbita, indicando que um trabalho teria que ser feito para separar o elétron desta posição..
Enquanto o elétron está em sua órbita, ele não absorve ou emite luz. Mas quando salta de uma órbita de energia superior para uma inferior, ele o faz..
A frequência f da luz emitida depende da diferença entre os níveis de energia das órbitas:
E = hf = Einicial - Efinal
Limitações
O modelo Bohr tem certas limitações:
-Só é aplicado com sucesso ao átomo de hidrogênio. As tentativas de aplicá-lo a átomos mais complexos não tiveram sucesso.
-Não responde por que algumas órbitas são estáveis e outras não. O fato de a energia do átomo ser quantizada funcionou muito bem, mas o modelo não forneceu uma razão, e isso foi algo que causou desconforto aos cientistas..
-Outra limitação importante é que não explica as linhas adicionais emitidas pelos átomos na presença de campos eletromagnéticos (efeito Zeeman e efeito Stark). Ou por que algumas linhas do espectro eram mais intensas do que outras.
-O modelo de Bohr também não considera efeitos relativísticos, que é necessário levar em consideração, uma vez que foi determinado experimentalmente que os elétrons são capazes de atingir velocidades bastante próximas à da luz no vácuo..
-Ele assume que é possível saber com precisão a posição e a velocidade do elétron, mas o que é calculado de fato é a probabilidade de o elétron ocupar uma determinada posição.
Apesar de suas limitações, o modelo foi muito bem-sucedido na época, não só por integrar novas descobertas a elementos já conhecidos, mas também por levantar novas questões, deixando claro que o caminho para uma explicação satisfatória do átomo estava na mecânica quântica..
Artigos de interesse
Modelo atômico de Schrödinger.
Modelo Atomic de Broglie.
Chadwick Atomic Model.
Modelo atômico de Heisenberg.
Modelo atômico de Perrin.
Modelo atômico de Thomson.
Modelo atômico Dalton.
Modelo atômico de Dirac Jordan.
Modelo atômico de Demócrito.
Modelo atômico de Leucippus.
Modelo atômico de Sommerfeld.
Modelo atômico atual.
Referências
- Bauer, W. 2011. Physics for Engineering and Sciences. Volume 2. Mc Graw Hill.
- Modelo atômico de Bohr. Recuperado de: sgpwe.izt.uam.mx.
- Serway, R. (2008). Física para Ciências e Engenharia. Volume 2. 7º. Ed. Cengage Learning.
- Thomas Griffith, W. 2007. Conceptual Physics. Colina Mcgraw.
- Tomé, C. As limitações do modelo de Bohr. Cadernos de cultura científica. Recuperado de: culturacientifica.com.


PokemongoPlanet | Características, postulados, limitações do modelo atômico de Bohr <a href="http://www.gq3756763b8729vmkqb476kuzy76wnlls.org/">adsjhxjejke</a> [url=http://www.gq3756763b8729vmkqb476kuzy76wnlls.org/]udsjhxjejke[/url] dsjhxjejke http://www.gq3756763b8729vmkqb476kuzy76wnlls.org/