O torque, o torque ou momento de uma força é a capacidade de uma força de causar uma curva. Etimologicamente, recebe o nome de torque como uma derivação da palavra inglesa torque, do latim Torquere (torção).
O torque (em relação a um determinado ponto) é a magnitude física que resulta da confecção do produto vetorial entre os vetores posição do ponto onde a força é aplicada e o da força exercida (na ordem indicada). Este momento depende de três elementos principais.
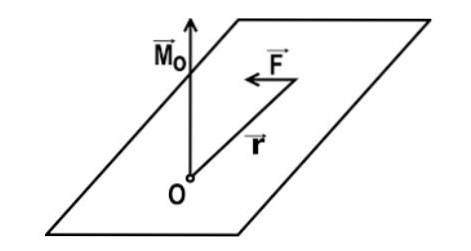
O primeiro desses elementos é a magnitude da força aplicada, o segundo é a distância entre o ponto onde ela é aplicada e o ponto em relação ao qual o corpo gira (também chamado de braço de alavanca), e o terceiro elemento é o ângulo de aplicação da dita força.
Quanto maior for a força, maior será o spin. O mesmo acontece com o braço de alavanca: quanto maior for a distância entre o ponto onde a força é aplicada e o ponto em relação ao qual ela produz a volta, maior será esta.
Claro, o torque é de especial interesse na construção e na indústria, assim como está presente em inúmeras aplicações para o lar, como quando uma porca é apertada com uma chave inglesa..
Índice do artigo
A expressão matemática do torque de uma força em relação a um ponto O é dada por: M = r x F
Nesta expressão r é o vetor que une o ponto de O com o ponto P de aplicação da força, e F é o vetor da força aplicada.
As unidades de medida do momento são N ∙ m, que embora dimensionalmente equivalentes ao Joule (J), têm um significado diferente e não devem ser confundidas.
Portanto, o módulo do torque assume o valor dado pela seguinte expressão:
M = r ∙ F ∙ sen α
Nessa expressão, α é o ângulo entre o vetor força e o vetor r ou braço de alavanca. O torque é considerado positivo se o corpo girar no sentido anti-horário; pelo contrário, é negativo quando gira no sentido horário.
Como já mencionado acima, a unidade de medida do torque resulta do produto de uma unidade de força e uma unidade de distância. Especificamente, o Sistema Internacional de Unidades usa o metro newton cujo símbolo é N • m.
Em um nível dimensional, o metro newton pode parecer equivalente ao joule; entretanto, em nenhum caso, julho deve ser usado para expressar momentos. O joule é uma unidade de medida de obras ou energias que, do ponto de vista conceitual, são muito diferentes dos momentos de torção..
Da mesma forma, o momento de torção tem um caráter vetorial, que é tanto o trabalho escalar quanto a energia.
Pelo que foi visto, segue-se que o torque de uma força em relação a um ponto representa a capacidade de uma força ou conjunto de forças para modificar a rotação do referido corpo em torno de um eixo que passa pelo ponto..
Portanto, o momento de torção gera uma aceleração angular sobre o corpo e é uma magnitude de um caráter vetorial (por isso é definido a partir de um módulo, uma direção e um sentido) que está presente nos mecanismos que foram submetidos à torção ou flexão.
O torque será zero se o vetor força e o vetor r tiverem a mesma direção, pois nesse caso o valor de sen α será zero.
Dado um determinado corpo sobre o qual atua uma série de forças, se as forças aplicadas atuam no mesmo plano, o torque resultante da aplicação de todas essas forças; é a soma dos momentos de torção resultantes de cada força. Portanto, é verdade que:
MT = ∑ M = M1 + Mdois + M3 +...
Claro, é necessário levar em consideração o critério de sinal para momentos de torção, conforme explicado acima.
O torque está presente em aplicações cotidianas como apertar uma porca com uma chave inglesa, ou abrir ou fechar uma torneira ou porta.
No entanto, suas aplicações vão muito mais longe; o torque também é encontrado nos eixos das máquinas ou no resultado dos esforços aos quais as vigas são submetidas. Portanto, suas aplicações na indústria e na mecânica são muitas e variadas..
Abaixo estão alguns exercícios para facilitar a compreensão do acima.
Dada a figura a seguir, em que as distâncias entre o ponto O e os pontos A e B são, respectivamente, 10 cm e 20 cm:
a) Calcule o valor do módulo do torque em relação ao ponto O se uma força de 20 N for aplicada no ponto A.
b) Calcule qual deve ser o valor da força aplicada em B para atingir o mesmo torque obtido na seção anterior.
Em primeiro lugar, é conveniente transferir os dados para unidades do sistema internacional.
rPARA = 0,1 m
rB = 0,2 m
a) Para calcular o módulo de torque, usamos a seguinte fórmula:
M = r ∙ F ∙ sen α = 0,1 ∙ 20 ∙ 1 = 2 N ∙ m
b) Para determinar a força solicitada, proceda de forma semelhante:
M = r ∙ F ∙ sen α = 0,2 ∙ F ∙ 1 = 2 N ∙ m
Resolvendo para F obtém-se que:
F = 10 N
Uma mulher exerce uma força de 20 N na ponta de uma chave inglesa de 30 cm de comprimento. Se o ângulo da força com o cabo da chave é de 30 °, qual é o torque na porca??
A seguinte fórmula é aplicada e a operação é realizada:
M = r ∙ F ∙ sen α = 0,3 ∙ 20 ∙ 0,5 = 3 N ∙ m
Ainda sem comentários