O movimento de linha uniforme ou em velocidade constante é aquele em que a partícula se move ao longo de uma linha reta e com velocidade constante. Desta forma, o móvel viaja distâncias iguais em tempos iguais. Por exemplo, se em 1 segundo você viajar 2 metros, após 2 segundos você terá viajado 4 metros e assim por diante.
Para fazer uma descrição precisa do movimento, seja ele retilíneo uniforme ou qualquer outro, é necessário estabelecer um ponto de referência, também denominado fonte, em relação ao qual o celular muda de posição.
Se o movimento ocorre inteiramente ao longo de uma linha reta, também é importante saber em que direção o corpo em movimento o percorre.
Em uma linha horizontal, é possível que o móbile vá para a direita ou para a esquerda. A distinção entre as duas situações é feita por sinais, sendo a convenção usual a seguinte: para a direita sigo (+) e para a esquerda sigo (-).
Quando a velocidade é constante, o móvel não muda sua direção ou sentido, e também a magnitude de sua velocidade permanece inalterada..
Índice do artigo
As principais características do movimento retilíneo uniforme (MRU) são as seguintes:
-O movimento sempre ocorre ao longo de uma linha reta.
-Um celular com MRU viaja distâncias ou espaços iguais em tempos iguais.
-A velocidade permanece inalterada tanto em magnitude quanto em direção e sentido.
-MRU não tem aceleração (sem mudança na velocidade).
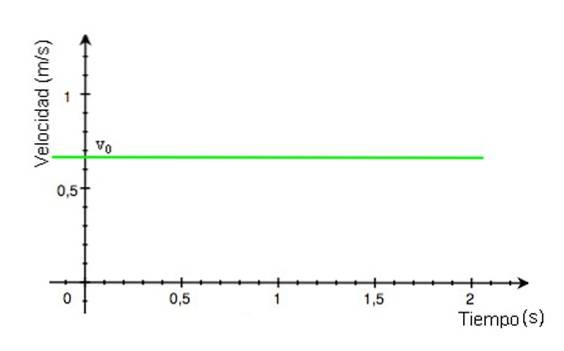
-Desde a velocidade v permanece constante ao longo do tempo t, o gráfico de sua magnitude em função do tempo é uma linha reta. No exemplo da figura 2, a linha é colorida de verde e o valor da velocidade é lido no eixo vertical, aproximadamente +0,68 m / s.
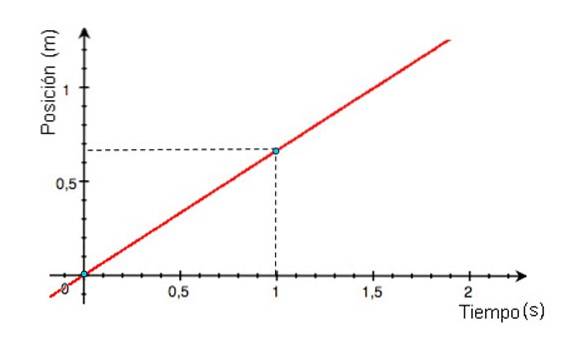
-O gráfico da posição x em relação ao tempo é uma linha reta, cuja inclinação é igual à velocidade do móvel. Se a linha do gráfico x vs t for horizontal, o móvel está em repouso, se a inclinação for positiva (gráfico da figura 3), a velocidade também é positiva.
Saiba a distância percorrida pelo celular quando o gráfico v vs. estiver disponível. t é muito simples. A distância percorrida é igual à área sob a linha e dentro do intervalo de tempo desejado.
Suponha que você queira saber a distância percorrida pelo celular na figura 2 no intervalo entre 0,5 e 1,5 segundos.
Esta área é a do retângulo sombreado da figura 4. É calculada encontrando o resultado da multiplicação da base do retângulo pela sua altura, cujos valores são lidos no gráfico.
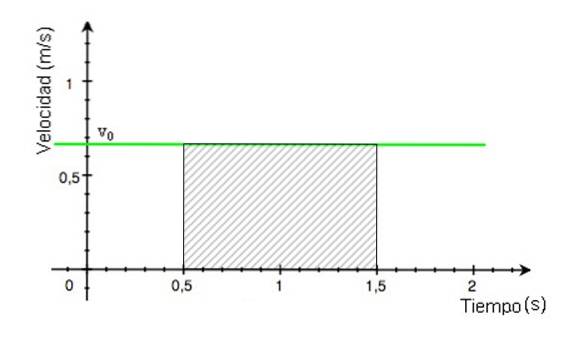
Distância percorrida = (1,5 - 0,5) x 0,68 m = 0,68 m
A distância é sempre uma quantidade positiva, independentemente de estar indo para a direita ou para a esquerda..
No MRU, a velocidade média e a velocidade instantânea são sempre as mesmas e, uma vez que seu valor é a inclinação do gráfico x vs t correspondente a uma linha, as equações correspondentes em função do tempo são as seguintes:
-Posição em função do tempo: x (t) = xou + vt
xou representa a posição inicial do móbile, muitas vezes coincide com a origem do sistema de referência, mas nem sempre é o caso. Esta equação também é conhecida como equação de itinerário.
-Velocidade em função do tempo: v (t) = constante
Quando v = 0 significa que o celular está em repouso. O descanso é um caso particular de movimento.
-Aceleração em função do tempo: a (t) = 0
No movimento retilíneo uniforme não há mudanças na velocidade, portanto, a aceleração é zero.
Ao resolver um exercício, certifique-se de que a situação corresponde ao modelo a ser utilizado. Em particular, antes de usar as equações MRU, é necessário certificar-se de que elas são aplicáveis.
Os seguintes exercícios resolvidos são problemas com dois celulares.
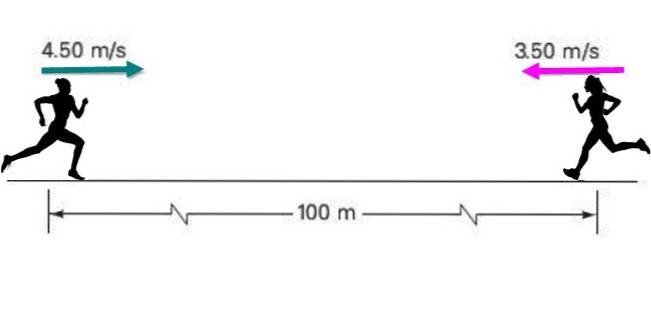
Dois atletas se aproximam com velocidade constante de 4,50 m / se 3,5 m / s respectivamente, inicialmente separados por uma distância de 100 metros, conforme indicado na figura.
Se cada um mantiver sua velocidade constante, descubra: a) Quanto tempo levam para se encontrarem? b) Qual será a posição de cada um naquele momento?
A primeira coisa é indicar a origem do sistema de coordenadas que servirá de referência. A escolha depende da preferência de quem resolve o problema..
Normalmente x = 0 é escolhido logo no ponto de partida dos celulares, pode ser no corredor esquerdo ou direito, pode até ser escolhido no meio de ambos.
a) Vamos escolher x = 0 no corredor esquerdo ou corredor 1, portanto a posição inicial deste é x01 = 0 e para o corredor 2 será x02 = 100 m. O corredor 1 se move da esquerda para a direita com velocidade v1 = 4,50 m / enquanto o corredor 2 faz isso da direita para a esquerda com uma velocidade de -3,50 m / s.
x1 = x01 + v1t1 = 4,50t1
xdois = x02 + vdoistdois = 100 -3,50tdois
Como o tempo é o mesmo para ambos t1 = tdois = t , quando se encontrarem, a posição de ambos será a mesma, portanto x1 = xdois. Coincidindo:
4,50t = 100 -3,50t
É uma equação de primeiro grau para o tempo, cuja solução é t = 12,5 s.
b) Os dois corredores estão na mesma posição, portanto, esta substituindo o tempo obtido na seção anterior em qualquer uma das equações de posição. Por exemplo, podemos usar o do corretor 1:
x1 = 4,50t1 = 56,25 m
O mesmo resultado é obtido substituindo t = 12,5 s na equação da posição para o corredor 2.
A lebre desafia a tartaruga a correr uma distância de 2,4 km e, para ser justa, dá-lhe meia hora de vantagem. No jogo, a tartaruga se move a uma taxa de 0,25 m / s, que é o máximo que ela consegue correr. Após 30 minutos, a lebre corre a 2 m / se alcança a tartaruga rapidamente.
Depois de continuar por mais 15 minutos, ela acha que tem tempo para tirar uma soneca e ainda assim vencer a corrida, mas adormece por 111 minutos. Quando acorda, corre com todas as forças, mas a tartaruga já cruza a linha de chegada. Achar:
a) Com que vantagem a tartaruga vence?
b) O instante de tempo em que a lebre ultrapassa a tartaruga
c) O momento em que a tartaruga ultrapassa a lebre.
A corrida começa em t = 0. A posição da tartaruga: xT = 0,25t
O movimento da lebre tem as seguintes partes:
-Descanse pela vantagem que deu à tartaruga: 0 < t < 30 minutos:
-Corra para alcançar a tartaruga e continue correndo um pouco depois de ultrapassá-la; no total são 15 minutos de movimento.
-Durma 111 minutos (descanso)
-Acorde tarde demaisarrancada final)
2,4 km = 2400 m
A duração da corrida foi: t = 2400 m / 0,25 m / s = 9600 s = 160 min. A partir desse momento tiramos 111 minutos do cochilo e 30 minutos à frente, o que perfaz 19 minutos (1140 segundos). Isso significa que você correu por 15 minutos antes de dormir e 4 minutos depois de acordar para o sprint.
Nesse tempo, a lebre percorreu a seguinte distância:
deu = 2 m / s. (15,60 s) + 2 m / s (4,60 s) = 1800 m + 480 m = 2280 m.
Como a distância total foi de 2.400 metros, subtraindo os dois valores, verifica-se que a lebre estava a 120 metros de alcançar a meta..
A posição da lebre antes de adormecer é xeu = 2 (t - 1800), considerando o atraso de 30 minutos = 1800 segundos. Correspondendo a xT e xeu encontramos o tempo em que estão:
2 (t - 1800) = 0,25t
2t -0,25 t = 3600
t = 2057,14 s = 34,29 min
No momento em que a lebre é alcançada pela tartaruga, ela adormece a 1.800 metros do início:
1800 = 0,25t
t = 7200 s = 120 min
O MRU é o movimento mais simples que se pode imaginar e por isso é o primeiro a ser estudado em cinemática, mas muitos movimentos complexos podem ser descritos como uma combinação deste e de outros movimentos simples..
Se uma pessoa sai de casa e dirige até chegar a uma longa estrada reta ao longo da qual viaja na mesma velocidade por um longo tempo, seu movimento pode ser descrito globalmente como um MRU, sem entrar em maiores detalhes.
Claro, a pessoa precisa fazer algumas curvas antes de entrar e sair da rodovia, mas usando este modelo de movimento, a duração da viagem pode ser estimada sabendo a distância aproximada entre o ponto de partida e o ponto de chegada..
Na natureza, a luz tem um movimento retilíneo uniforme cuja velocidade é de 300.000 km / s. Da mesma forma, o movimento do som no ar pode ser assumido como retilíneo uniforme com uma velocidade de 340 m / s em muitas aplicações..
Ao analisar outros problemas, por exemplo, o movimento dos portadores de carga dentro de um fio condutor, a aproximação MRU também pode ser usada para dar uma ideia do que acontece dentro do condutor..
Ainda sem comentários