
Características de movimento retilíneo uniformemente acelerado, fórmulas
O movimento retilíneo uniformemente acelerado É aquele que segue em linha reta e em que o móbile aumenta ou diminui sua velocidade a uma taxa constante. Esta taxa é a magnitude que descreve a taxa com a qual a velocidade muda e é chamada aceleração.
No caso de movimento retilíneo uniformemente acelerado ou variado (MRUV), a aceleração constante é responsável por alterar a magnitude da velocidade. Em outros tipos de movimento, a aceleração também é capaz de mudar a direção e o sentido da velocidade, ou mesmo apenas mudar a direção, como no movimento circular uniforme..

Uma vez que a aceleração representa a mudança na velocidade ao longo do tempo, suas unidades no Sistema Internacional são m / sdois (metros em segundos ao quadrado). Assim como a velocidade, a aceleração pode receber um sinal positivo ou negativo, dependendo se a velocidade aumenta ou diminui..
Uma aceleração de, digamos, +3 m / sdois significa que para cada segundo que passa, a velocidade do móvel aumenta em 3 m / s. Se no início do movimento (em t = 0) a velocidade do móbile era +1 m / s, depois de um segundo será de 4 m / se após 2 segundos será de 7 m / s.
No movimento retilíneo uniformemente variado, as variações na velocidade que os objetos em movimento experimentam diariamente são levadas em consideração. Este é um modelo mais realista do que o movimento retilíneo uniforme. Mesmo assim, ainda é bastante limitado, pois restringe o celular a viajar apenas em linha reta.
Índice do artigo
- 1 recursos
- 1.1 Distância percorrida do gráfico v vs. t
- 2 Fórmulas e equações
- 3 exercícios resolvidos
- 3.1 - Exercício resolvido 1
- 3.2 - Exercício resolvido 2
- 4 aplicativos
- 5 referências
Caracteristicas
Estas são as principais características do movimento retilíneo uniformemente acelerado:
-O movimento sempre ocorre ao longo de uma linha reta.
-A aceleração do celular é constante, tanto em magnitude quanto em direção e sentido.
-A velocidade móvel aumenta (ou diminui) linearmente.
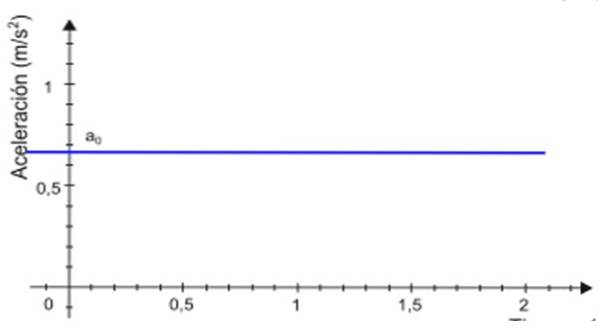
-Desde a aceleração para permanece constante ao longo do tempo t, o gráfico de sua magnitude em função do tempo é uma linha reta. No exemplo mostrado na figura 2, a linha é colorida em azul e o valor de aceleração é lido no eixo vertical, aproximadamente +0,68 m / sdois.
-O gráfico de velocidade v cerca de t é uma linha reta (em verde na figura 3), cuja inclinação é igual à aceleração do móbile. No exemplo, a inclinação é positiva.

-O corte com o eixo vertical indica a velocidade inicial, neste caso é de 0,4 m / s.
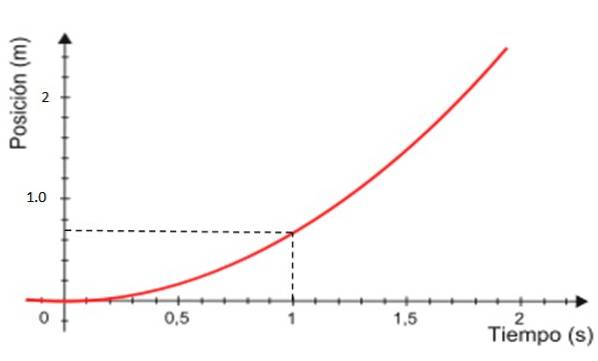
-Finalmente, o gráfico da posição x versus tempo é a curva mostrada em vermelho na figura 4, que é sempre uma parábola.
Distância percorrida do gráfico v vs. t
Tendo o gráfico v vs. t, calcular a distância percorrida pelo celular é muito fácil. A distância percorrida é igual à área sob a linha que está dentro do intervalo de tempo desejado.
No exemplo mostrado, suponha que você queira saber a distância percorrida pelo celular entre 0 e 1 segundo. Usando este gráfico, veja a Figura 5.
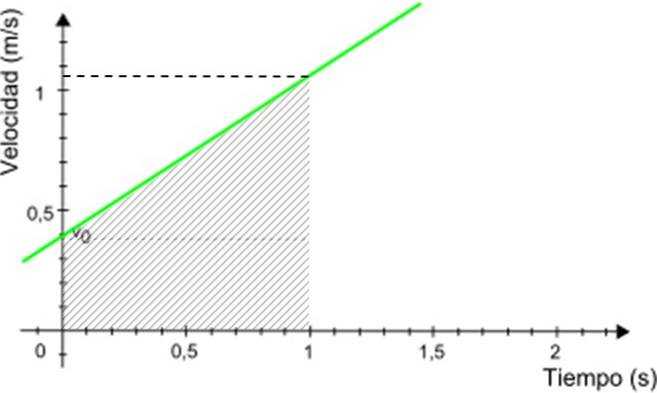
A distância procurada é numericamente equivalente à área do trapézio sombreado na figura 3. A área do trapézio é dada por: (base maior + base menor) x altura / 2
Distância percorrida = (0,4 + 1,05) x 1/2 m = 0,725 m
Também é possível dividir a área sombreada em um triângulo e um retângulo, calcular as áreas correspondentes e adicioná-las. A distância percorrida é positiva, mesmo que a partícula vá para a direita ou para a esquerda.
Fórmulas e equações
Tanto a aceleração média quanto a aceleração instantânea têm o mesmo valor no MRUV, portanto:
-Aceleração: para = constante
Quando a aceleração é igual a 0 o movimento é retilíneo uniforme, já que a velocidade seria constante neste caso. O sinal de para Pode ser positivo ou negativo.
Uma vez que a aceleração é a inclinação da linha v versus t, a equação v (t) é:
-Velocidade em função do tempo: v (t) = vou + no
Onde vou é o valor da velocidade inicial do celular
-Posição em função do tempo: x (t) = xou + vou t + ½atdois
Quando você não tem tempo, mas em vez disso tem velocidades e deslocamentos, existe uma equação muito útil que é obtida resolvendo o tempo de v (t) = vou + no e substituindo-o na última equação. Se trata de:
-Equação que não contém tempo: vdois = voudois +2.a.Δx
Exercícios resolvidos
Ao resolver um exercício de cinemática, é importante certificar-se de que a situação está adaptada ao modelo a ser usado. Por exemplo, as equações de movimento retilíneo uniforme não são válidas para movimento acelerado.
E aqueles do movimento acelerado não valem para um movimento circular ou curvilíneo, por exemplo. O primeiro desses exercícios resolvidos a seguir combina dois móbiles com movimentos diferentes. Para resolvê-lo corretamente, é necessário ir ao modelo de movimento adequado.
-Exercício 1 resolvido
Para saber a profundidade de um poço, a criança deixa cair uma moeda e ao mesmo tempo ativa o cronômetro, que pára logo após ouvir a moeda caindo na água. Sua leitura foi de 2,5 segundos. Sabendo que a velocidade do som no ar é 340 m / s, calcule a profundidade do poço.
Solução
Ser h a profundidade do poço. A moeda percorre esta distância em queda livre, um movimento vertical uniformemente variado, com velocidade inicial 0, à medida que a moeda é jogada, e aceleração descendente constante igual a 9,8 m / sdois. Tomar um tempo tm em fazer isso.
Assim que a moeda atinge a água, o som do clique sobe até o ouvido da criança, que para o cronômetro ao ouvi-lo. Não há razão para acreditar que a velocidade do som muda conforme ele sobe no poço, então o movimento do som é retilíneo uniforme. O som demora um pouco ts para chegar à criança.
Equação de movimento da moeda:
h = ½.g.tm dois = 4,9 tm dois
Onde eles foram substituídos x Y para da equação para a posição dada na seção anterior, por h Y g.
Equação de movimento para som:
h = vs . ts = 340 ts
É sobre a equação familiar distância = velocidade x tempo. Com essas duas equações, temos três incógnitas: h, tm e ts. Nas vezes em que há relacionamento, sabe-se que tudo leva 2,5 segundos para acontecer, portanto:
tm + ts = 2,5 s
Equacionando as duas equações:
4,9 tm dois = 340 ts
Limpando um dos tempos e substituindo:
4,9 tm dois= 340. (2,5 - tm)
Ao desenvolver o termo à direita e transpor os termos, obtemos:
4,9 tm dois+340 tm - 850 = 0
Esta é uma equação quadrática com duas soluções: 2,416 e -71,8. Escolhe-se a solução positiva, que é a que faz sentido, já que o tempo não pode ser negativo e em qualquer caso deve ser inferior a 2,5 segundos. Para este tempo é obtido substituindo a profundidade do poço:
4,9 tm dois= 4,9 x 2,416dois m = 28,6 m
-Exercício resolvido 2
Um carro viajando a 90 km / h está se aproximando de uma rua transversal com um semáforo. Quando estiver a 70 m dali, acende-se a luz amarela, que dura 4 segundos. A distância entre o semáforo e a próxima esquina é de 50 m.
O motorista tem estas duas opções: a) freio a - 4 m / sdois ou b) acelerar para + 2 m / sdois. Qual das duas opções permite ao motorista parar ou atravessar toda a avenida antes que o semáforo fique vermelho?
Solução
A posição inicial do motorista é x = 0 apenas quando ele vê a luz amarela acender. É importante converter as unidades corretamente: 90 km / h é igual a 25 m / s.
De acordo com a opção a), nos 4 segundos que dura o sinal amarelo, o motorista se desloca:
x (t) = vou t + ½atdois= 25,4 -½. (- 4) .4doism = 68 m (Para 2 metros antes do semáforo)
Analisando a opção b), temos:
x (t) = vou t + ½atdois= 25.t + ½.2.tdois
Enquanto dura a luz amarela, o motorista se desloca desta forma:
x = 25,4 + ½,2,4doism = 116 m
Porém, 116 m é menor que a distância disponível para chegar à próxima esquina, que é 70 + 50 m = 120 m, portanto, ele não pode atravessar a rua inteira antes que o sinal vermelho acenda. A ação recomendada é frear e ficar a 2 metros do semáforo.
Formulários
As pessoas vivenciam os efeitos da aceleração diariamente: ao viajar de carro ou ônibus, pois estes precisam frear e acelerar continuamente para adaptar a velocidade aos obstáculos da estrada. A aceleração também é sentida ao subir ou descer em um elevador.
Parques de diversão são lugares onde as pessoas pagam para experimentar os efeitos da aceleração e se divertir.
Na natureza, o movimento retilíneo uniformemente variado é observado quando um objeto é largado livremente ou quando é jogado verticalmente para cima e aguardado para retornar ao solo. Se a resistência do ar for desprezada, o valor da aceleração é o da gravidade: 9,8 m / s2.
Referências
- Bauer, W. 2011. Physics for Engineering and Sciences. Volume 1. Mc Graw Hill. 40-45.
- Figueroa, D. Série de Física para Ciências e Engenharia. Volume 3. Edição. Cinemática. 69-85.
- Giancoli, D. Física: Princípios com Aplicações. 6º. Ed Prentice Hall. 19-36.
- Hewitt, Paul. 2012. Ciência Física Conceitual. 5º. Ed. Pearson. 14-18.
- Kirkpatrick, L. 2007. Physics: A Look at the World. 6ta Edição reduzida. Cengage Learning. 15-19.
- Wilson, J. 2011. Physics 10. Pearson Education. 116-119


Ainda sem comentários