
Movimento relativo em uma dimensão, em duas dimensões, exercícios
O movimento relativo de uma partícula ou de um objeto é aquele que é observado em relação a um determinado ponto de referência que o observador escolheu, que pode ser fixo ou em movimento. Velocidade sempre se refere a algum sistema de coordenadas usado para descrevê-lo.
Por exemplo, o passageiro de um carro em movimento e que viaja confortavelmente adormecido em seu assento está em repouso em relação ao motorista, mas não para um observador parado na calçada que vê o carro passar..

Então o movimento é sempre relativo, mas acontece que em geral o sistema de coordenadas ou referência é escolhido tendo sua origem na Terra ou no solo, local considerado estacionário. Dessa forma, a preocupação se concentra em descrever o movimento do objeto em estudo..
É possível descrever a velocidade do copiloto adormecido em comparação com um passageiro viajando em outro carro? A resposta é sim. Existe liberdade para escolher o valor de (xou, You, zou): a origem do sistema de referência. A seleção é arbitrária e depende da preferência do observador, bem como da facilidade que ela proporciona para a resolução do problema..
Índice do artigo
- 1 Movimento relativo em uma dimensão
- 1.1 - Exemplo trabalhado 1
- 2 Movimento relativo em duas e três dimensões
- 2.1 - Exercício resolvido 2
- 2.2 - Exercício resolvido 3
- 3 referências
Movimento relativo em uma dimensão
Quando o movimento ocorre em linha reta, os móbiles têm velocidades na mesma direção ou na direção oposta, ambas vistas por um observador em pé na Terra (T). O observador se move em relação aos celulares? Sim, com a mesma velocidade que carregam, mas na direção oposta.
Como um celular se move em relação ao outro? Para descobrir, as velocidades são adicionadas vetorialmente.
-Exemplo trabalhado 1
Referindo-se à figura mostrada, indique a velocidade relativa do carro 1 em relação ao carro 2 em cada situação.
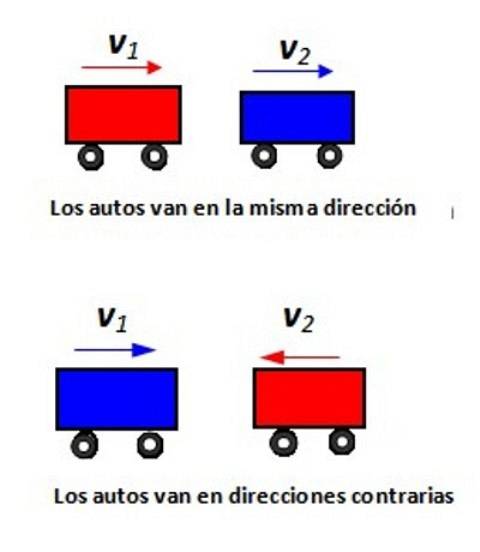
Solução
Iremos atribuir um sinal positivo às velocidades à direita e um sinal negativo à esquerda. Se um celular for para a direita a 80 km / h, um passageiro neste celular verá o observador na Terra se mover a - 80 km / h.
Suponha que tudo aconteça ao longo do eixo x. Na figura a seguir, o carro vermelho está se movendo a +100 km / h (visto de T) e está prestes a ultrapassar o carro azul viajando a +80 km / h (visto também de T). Quão rápido um passageiro no carro azul se aproxima do carro vermelho?
Os rótulos são: v 1/2 velocidade do carro 1 em relação ao carro 2, v1 / T velocidade do carro em relação a T, vT / 2 velocidade de T em relação a 2. Adição de vetor:
v1/2 = v1 / T + vT / 2 = (+100 km / h - 80 km / h) x= 20 km / h x
Podemos fazer sem a notação vetorial. Observe os subscritos: multiplicando os dois da direita você deve obter o da esquerda.
E quando eles vão para o outro lado? Agora v1 / T = + 80 km / he v2 / T = -100 km / h, portanto vT / 2 = + 100 km / h. O passageiro do carro azul verá a abordagem do carro vermelho:
v1/2 = v1 / T + vT / 2 = +80 km / h +100 km / h = 180 km / h
Movimento relativo em duas e três dimensões
No esquema a seguir, r é a posição do avião vista do sistema X e Z, r'é a posição do sistema X e Z ' Y R é a posição do sistema com prêmio em relação ao sistema sem prêmio. Os três vetores formam um triângulo em que R + r'= r, portanto r'= r - R.
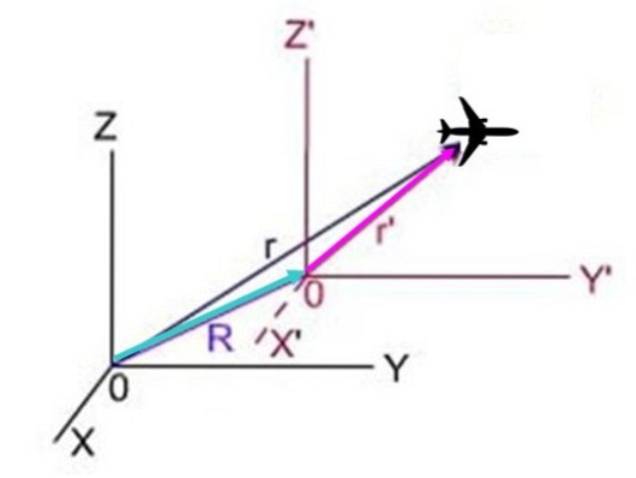
Uma vez que a derivada em relação ao tempo da posição é precisamente a velocidade, resulta:
v'= v - ou
Nesta equação v'é a velocidade do avião em relação ao sistema X e Z ', v é a velocidade em relação ao sistema X e Z Y ou é a velocidade constante do sistema primário em relação ao sistema não acionado.
-Exercício resolvido 2
Um avião está indo para o norte com velocidade no ar de 240 km / h. De repente, o vento começa a soprar de oeste para leste a uma velocidade de 120 km / dependendo da terra.
Encontre: a) A velocidade do avião com respeito ao solo, b) O desvio experimentado pelo piloto c) A correção que o piloto deve fazer para poder mirar diretamente ao norte e a nova velocidade com respeito ao solo, uma vez a correção foi feita.
Solução
a) Existem os seguintes elementos: plano (A), solo (T) e vento (V).
No sistema de coordenadas em que o norte é a direção + y e a direção oeste-leste é + x, temos as velocidades fornecidas e seus respectivos rótulos (subscritos):
v AV = 240 km / h (+Y); v V / T = 120 km / h (+x); v NO = ?
A soma vetorial adequada é:
v NO = v AV + v V / T = 240 km / h (+Y) + 120 km / h (+x)
A magnitude deste vetor é: v NO = (240 dois+ 120dois)1/2 km / h = 268,3 km / h
b) θ = arctg (v AV / v V / T) = arctg (240/120) = 63,4º Norte de Leste ou 26,6º Nordeste.
c) Para continuar para o norte com este vento, você precisará apontar a proa da aeronave para o noroeste, de modo que o vento o empurre diretamente para o norte. Neste caso, a velocidade do avião visto do solo será na direção + y, enquanto a velocidade do avião em relação ao vento será de noroeste (não precisa necessariamente ser 26,6º).
Pelo teorema de Pitágoras:
v NO = (240 dois- 120dois)1/2 km / h = 207,8 km / h
α = arctg (v V / T / v NO ) = arctg (120 / 207,8) = 30º Noroeste
-Exercício resolvido 3
Uma pessoa leva 2 minutos para descer uma escada rolante estacionária. Se a escada funcionar, a pessoa leva 1 minuto para descer enquanto está parada. Quanto tempo leva para a pessoa descer com a escada correndo?
Solução
Existem três elementos a serem considerados: a pessoa (P), a escada (E) e o solo (S), cujas velocidades relativas são:
vEDUCAÇAO FISICA : velocidade da pessoa em relação à escada; vISSO É: velocidade da escada em relação ao solo; vP / S: velocidade da pessoa em relação ao solo.
Visto do solo por um observador fixo, a pessoa que desce a escada (E) tem uma velocidade v P / S dado por:
v P / S = vEDUCAÇAO FISICA + vISSO É
A direção positiva está descendo a escada. Ser t o tempo que leva para descer e eu a distância. A magnitude da velocidade da pessoa v P / S isso é:
vP / S = L / t
t1 é o tempo que leva para descer com a escada parada: v EDUCAÇAO FISICA = L / t1
E Tdois aquele que o leva para baixo ainda na escada móvel: v ISSO É = L / tdois
Combinando as expressões:
L / t = L / t1 + L / tdois
Substituindo valores numéricos e resolvendo t:
1 / t = 1 / t1 + 1 / tdois = 1/2 + 1/1 = 1,5
Portanto, t = 1 / 1,5 minutos = 40 segundos.
Referências
- Bauer, W. 2011. Physics for Engineering and Sciences. Volume 1. Mc Graw Hill. 84-88.
- Figueroa, D. Série de Física para Ciências e Engenharia. Volume 3. Edição. Cinemática. 199-232.
- Giancoli, D. 2006. Física: Princípios com Aplicações. 6º. Ed. Prentice Hall. 62-64.
- Movimento relativo. Recuperado de :ourses.lumenlearning.com
- Wilson, J. 2011. Physics 10. Pearson Education. 166-168.



Ainda sem comentários