
Características, vantagens e desvantagens do método de custo mínimo

O método de menor custo é um procedimento usado para obter a solução inicial viável para um problema de transporte. Usado quando a prioridade é reduzir os custos de distribuição do produto.
O método de menor custo busca atingir o menor custo de transporte entre vários centros de demanda (os destinos) e vários centros de abastecimento (as fontes)..

A capacidade de produção ou abastecimento de cada fonte, bem como a necessidade ou demanda de cada destino são conhecidas e fixas..
O custo de transporte de uma unidade do produto de cada origem até cada destino também é conhecido..
O produto deve ser transportado de diversas origens para diferentes destinos de forma a atender a demanda de cada destino e, ao mesmo tempo, minimizar o custo total do transporte..
Outros métodos podem ser usados se a prioridade for economia de tempo em vez de economia de custos.
Índice do artigo
- 1 recursos
- 1.1 Etapas do método de menor custo
- 1.2 Aplicativos
- 2 vantagens
- 3 desvantagens
- 4 exemplo
- 4.1 Explicação do método
- 5 referências
Caracteristicas
A alocação ótima de um produto de várias origens para destinos diferentes é chamada de problema de transporte..
- Os modelos de transporte tratam do transporte de um produto fabricado em diferentes plantas ou fábricas (fontes de abastecimento) para vários armazéns (destinos de demanda).
- O objetivo é atender às necessidades dos destinos dentro das limitações da capacidade produtiva das fábricas, com um custo mínimo de transporte..
Etapas do método de menor custo
Passo 1
A célula que contém o menor custo de transporte em toda a tabela é selecionada. Essa célula é atribuída a tantas unidades quanto possível. Essa quantidade pode ser limitada por restrições de oferta e demanda..
Caso várias células tenham o menor custo, será selecionada a célula onde a alocação máxima pode ser feita.
Em seguida, procedemos ao ajuste da oferta e da demanda que está na linha e coluna afetadas. É ajustado subtraindo-se o valor atribuído à célula.
Passo 2
A linha ou coluna em que a oferta ou demanda foi esgotada (seja zero) é eliminada.
Caso ambos os valores, oferta e demanda, sejam iguais a zero, qualquer linha ou coluna pode ser eliminada, arbitrariamente.
etapa 3
As etapas anteriores são repetidas com o próximo custo mais baixo e continuam até que todo o fornecimento disponível nas diferentes origens ou toda a demanda dos diferentes destinos seja satisfeita..
Formulários
- Minimize os custos de transporte das fábricas para os armazéns ou dos armazéns para as lojas de varejo.
- Determine o local de menor custo de uma nova fábrica, depósito ou escritório de vendas.
- Determine o cronograma de produção de custo mínimo que atenda a demanda da empresa com limitações de produção.
Vantagem
O método de menor custo é considerado para produzir resultados mais precisos e ideais em comparação com o do canto noroeste.
Isso ocorre porque o método do canto noroeste apenas leva em consideração os requisitos de fornecimento e disponibilidade, com o canto superior esquerdo como subsídio inicial, independentemente do custo de envio..
Por outro lado, o método de custo mínimo inclui os custos de transporte durante a realização das atribuições..
- Ao contrário do método do canto noroeste, este método fornece uma solução precisa, pois considera o custo de transporte ao mapear.
- O método de menor custo é um método muito simples de usar.
- É muito simples e fácil calcular a solução ótima com este método.
- O método de menor custo é muito fácil de entender.
Desvantagens
- Para obter a solução ideal, certas regras devem ser seguidas. No entanto, o método de menor custo não os segue passo a passo.
- O método de menor custo não segue nenhuma regra sistemática quando há empate no menor custo.
- O método de menor custo permite a seleção por meio da observação da equipe, o que pode criar mal-entendidos para obter a solução ideal.
- Ele não tem a capacidade de fornecer nenhum tipo de critério para determinar se a solução obtida com esse método é ou não a mais ótima..
- As quantidades de ofertas e demandas são sempre as mesmas, pois não variam com o tempo..
- Não leva em consideração outros tipos de fatores a serem atribuídos, mas apenas o dos custos de transporte.
Exemplo
O conceito de método de menor custo pode ser entendido por meio do seguinte problema:
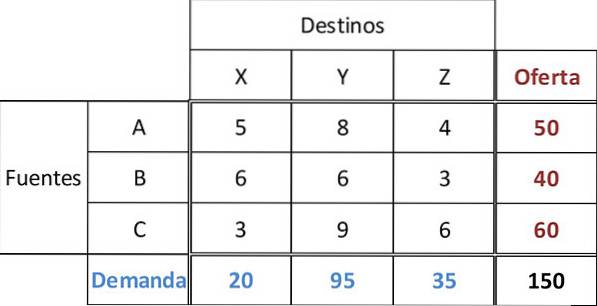
Nesta tabela, o fornecimento de cada fonte A, B, C é de 50, 40 e 60 unidades, respectivamente. A demanda dos três varejistas X, Y, Z é de 20, 95 e 35 unidades, respectivamente. Para todas as rotas, o custo de transporte é dado.
O custo mínimo de transporte pode ser obtido seguindo as etapas abaixo:
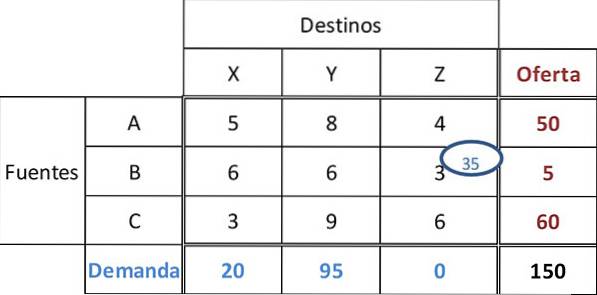
O custo mínimo da tabela é 3, com empate nas células BZ e CX. Geralmente, para obter a melhor solução inicial, o custo deve ser escolhido onde a maior quantidade pode ser alocada.
Portanto, 35 unidades serão atribuídas à célula BZ. Isso satisfaz a demanda do varejista Z, deixando 5 unidades na fonte B.
Explicação do método
Novamente, o custo mínimo é 3. Portanto, 20 unidades serão atribuídas à célula CX. Isso atende a demanda do varejista X, deixando 40 unidades na fonte C.
O próximo custo mínimo é 4. No entanto, a demanda por Z já foi concluída. Vamos para o próximo custo mínimo, que é 5. Além disso, a demanda por X já foi concluída.
O próximo custo mínimo é 6, com um empate entre três células. No entanto, você não pode atribuir unidades às células BX e CZ, porque a demanda dos varejistas X e Z é atendida. Em seguida, 5 unidades são atribuídas à célula BY. Isso completa o fornecimento da fonte B.
O próximo custo mínimo é 8, atribuindo 50 unidades à célula AY, completando o fornecimento da fonte A.
O próximo custo mínimo é de 9. 40 unidades são atribuídas à célula CY, completando assim a demanda e o fornecimento para todos os destinos e fontes. A tarefa final resultante é:
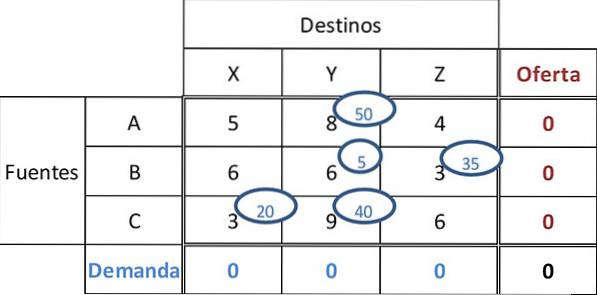
O custo total pode ser calculado multiplicando os valores atribuídos pelos custos nas células correspondentes: Custo total = 50 * 8 + 5 * 6 + 35 * 3 + 20 * 3 + 40 * 9 = 955.
Referências
- Jargons de negócios (2019). Método de menor custo. Retirado de: businessjargons.com.
- Consultoria de Atribuição (2019). Ajuda para atribuição do método de menor custo. Retirado de: assignconsultancy.com.
- Gestão de Negócios (2015). Problema de transporte. Retirado de: engineering-bachelors-degree.com.
- Josefina Pacheco (2019). Qual é o método de menor custo? Web e empresas. Retirado de: webyempresas.com.
- Atozmath (2019). Exemplo de método de menor custo. Retirado de: cbom.atozmath.com.


Ainda sem comentários