O método de paralelogramo é um método gráfico para adicionar dois vetores no plano. É frequentemente utilizado para encontrar a resultante de duas forças aplicadas a um corpo ou de duas velocidades, como no caso de um nadador que pretende atravessar um rio perpendicularmente e é desviado pela corrente..
Para construir o paralelogramo, as origens dos vetores a serem adicionados, desenhados em escala, devem coincidir em um ponto.
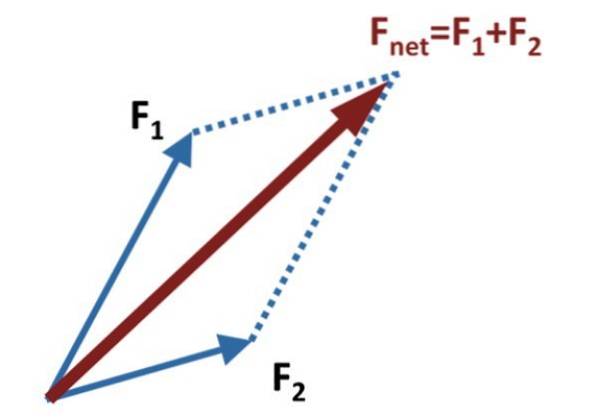
Em seguida, linhas auxiliares são traçadas paralelas a cada vetor, chegando ao final do outro, conforme mostrado na figura acima.
A soma ou vetor resultante, também chamado de força resultante, é o vetor Finternet, que é obtido desenhando o vetor que vai da origem comum de F1 Y Fdois, até o ponto onde as linhas paralelas auxiliares se cruzam. No diagrama da figura, eles são representados por linhas pontilhadas.
O método recebe o nome da figura que é formada com os vetores adendos e as linhas auxiliares, que é precisamente um paralelogramo. A diagonal principal do paralelogramo é o vetor de soma.
É muito importante notar que a ordem em que os vetores adendos são colocados não altera a soma em nada, uma vez que esta operação entre os vetores é comutativa..
Índice do artigo
A imagem a seguir mostra os vetores v Y ou em unidades arbitrárias. O vetor v mede 3,61 unidades e forma um ângulo de 56,3º com a horizontal, enquanto ou mede 6,32 unidades e um ângulo de 18,4º em relação à referida linha de referência.
Vamos encontrar sua soma vetorial usando o método do paralelogramo.
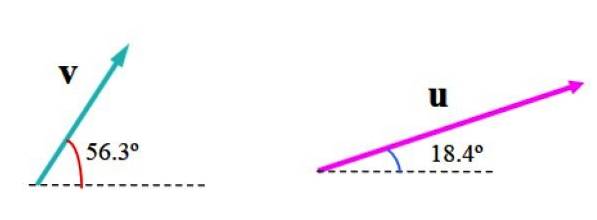
Escolha uma escala apropriada, como a mostrada na figura a seguir, na qual o plano foi dividido por uma grade. A largura do quadrado representa uma (1) unidade.
Como os vetores não são alterados na translação, eles são posicionados de forma que suas origens coincidam com a origem do sistema de coordenadas (imagem à esquerda).
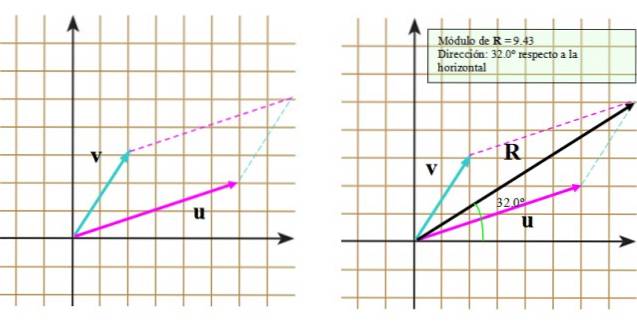
Agora vamos seguir estas etapas:
O resultado pode ser visto na imagem certa, na qual o vetor resultante aparece R.
Se quisermos saber a magnitude de R, podemos medir seu comprimento e compará-lo com a escala que temos. E quanto à sua direção, o eixo horizontal ou o eixo vertical podem ser usados como referências, por exemplo.
Ao usar o eixo horizontal ou eixo x, o ângulo que R forma com o referido eixo é medida com o transferidor e, desta forma, sabemos a direção de R.
Da mesma forma, a magnitude e direção de R pode ser calculado usando os teoremas do cosseno e do seno, uma vez que o paralelogramo formado pode ser dividido em dois triângulos congruentes, cujos lados são os módulos dos vetores ou, v Y R. Veja o exemplo 1 trabalhado.
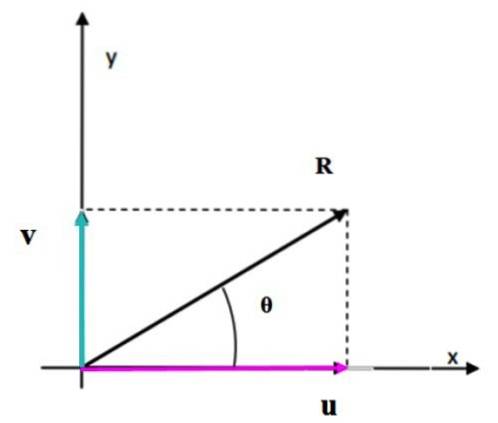
Quando os vetores são perpendiculares entre si, a figura que se forma é um retângulo. O módulo do vetor resultante corresponde ao comprimento da diagonal, que pode ser facilmente calculado usando o teorema de Pitágoras.
Nós temos o vetor v, que mede 3,61 unidades e forma um ângulo de 56,3º com a horizontal, e o vetor ou, cuja medida é 6,32 unidades e forma um ângulo de 18,4º (figura 2). Determine o módulo do vetor resultante R = ou + v e a direção que o vetor forma com o eixo horizontal.
O método do paralelogramo é aplicado de acordo com as etapas descritas acima, para a obtenção do vetor R. Como dito antes, se os vetores forem cuidadosamente desenhados seguindo a escala e usando a régua e o transferidor, a magnitude e a direção de R são medidos diretamente no desenho.
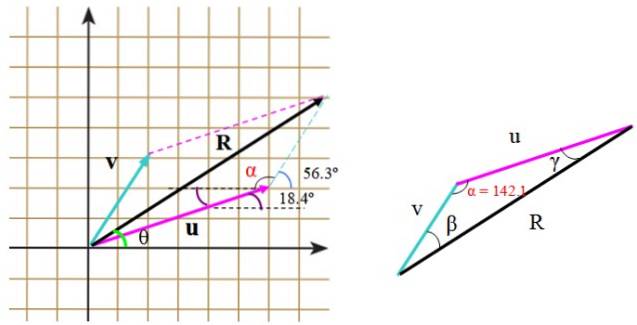
Eles também podem ser calculados diretamente, com a ajuda da trigonometria e das propriedades dos ângulos. Quando o triângulo formado não está certo, como neste caso, o teorema do cosseno é aplicado para encontrar o lado que falta.
No triângulo da direita, os lados medem u, v e R. Para aplicar o teorema do cosseno é necessário conhecer o ângulo entre v Y ou, que podemos encontrar com a ajuda da grade, posicionando adequadamente os ângulos fornecidos pela declaração.
Este ângulo é α e é composto por:
α = (90-56,3º) + 90º + 18,4º = 142,1º
De acordo com o teorema do cosseno:
Rdois = vdois + oudois - 2u⋅v⋅cos α = 3,61dois + 6,32dois - 2 × 3,61 × 6,32 × cos 142,1º = 88,98
R = 9,43 unidades.
Finalmente, o ângulo entre R e o eixo horizontal é θ = 18,4 º + γ. O ângulo γ pode ser encontrado usando o teorema do seno:
sin α / R = sin γ / u
Portanto:
sin γ = v (sin α / R) = 3,61 x (sin 142,1º / 9,43)
γ = 13,6º
θ = 18,4º + 13,6º = 32º
Um nadador está prestes a cruzar um rio nadando perpendicularmente à corrente com uma velocidade constante de 2,0 m / s. O nadador parte de A, porém termina em B, um ponto a jusante, devido à corrente que o desviou.
Se a velocidade da corrente for 0,8 m / se todas as velocidades forem assumidas constantes, encontre a velocidade do nadador vista por um observador parado na costa.
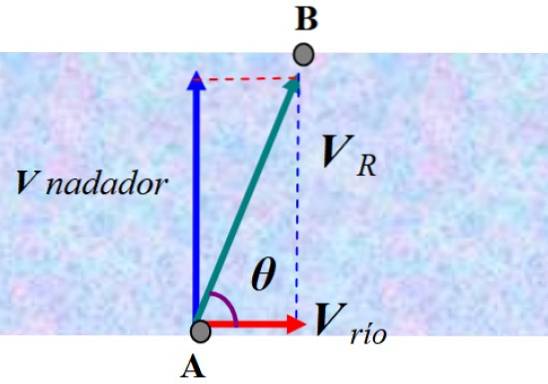
Um observador parado na costa veria como o nadador é desviado de acordo com a velocidade resultante VR. Para encontrar a resposta, precisamos somar vetorialmente a velocidade do nadador em relação à água e a velocidade da corrente, que chamamos de V Rio:
V R = V nadador + V Rio
Na figura, que não está em escala, os vetores foram somados para obter V R. Neste caso, o teorema de Pitágoras pode ser aplicado para obter sua magnitude:
VRdois = 2,0dois + 0,8dois = 4,64
VR = 2,15 m / s
A direção na qual o nadador se desvia da direção perpendicular é facilmente calculada, observando que:
θ = arctg (2 / 0,8) = 68,2º
Então o nadador desvia 90º - 68,2º = 27,2º de sua direção original.
Ainda sem comentários