
Método de Trachtenberg em que consiste, exemplos
O Método Trachtenberg é um sistema para realizar operações aritméticas, principalmente multiplicação, de forma fácil e rápida, uma vez que suas regras são conhecidas e dominadas.
Foi idealizado pelo engenheiro russo Jakow Trachtenberg (1888-1953) quando ele era prisioneiro dos nazistas em um campo de concentração, como uma forma de distração para manter a sanidade enquanto continuava no cativeiro..
Índice do artigo
- 1 Em que consiste, vantagens e desvantagens
- 2 exemplos
- 2.1 - Multiplique um número por 10 ou por 11
- 2.2 - Multiplicação por números de 12 a 19
- 2.3 - Extensão das regras de multiplicação por 13, ... até 19
- 3 regras para produtos por 6, 7 e 5
- 3.1 - Multiplicação por 6
- 3.2 - Multiplicação por 7
- 3.3 - Multiplicação por 5
- 4 regras para produtos por 9
- 5 Multiplicação por 8, 4, 3 e 2
- 5.1 - Multiplicação por 8
- 5.2 - Multiplicação por 4
- 5.3 - Multiplicação por 3
- 5.4 - Multiplicação por 2
- 6 Multiplique por figuras compostas
- 6.1 Exercício
- 7 referências
Em que consiste, vantagens e desvantagens
A vantagem deste método é que para efetuar a multiplicação não é necessário memorizar as tabuadas, pelo menos em parte, basta saber contar e somar, bem como dividir um algarismo por dois..
A desvantagem é que não existe uma regra universal para a multiplicação por qualquer número, em vez disso, a regra varia de acordo com o multiplicador. No entanto, os padrões não são difíceis de memorizar e, em princípio, permitem que as operações sejam realizadas sem a ajuda de papel e lápis..
Ao longo deste artigo, vamos nos concentrar nas regras para multiplicar rapidamente.
Exemplos
Para aplicar o método é necessário conhecer as regras, por isso vamos apresentá-las uma a uma e com exemplos:
- Multiplique um número por 10 ou por 11
Regra para multiplicar por 10
-Para multiplicar qualquer número por 10, basta adicionar um zero à direita. Por exemplo: 52 x 10 = 520.
Regras para multiplicação por 11
-Um zero é adicionado ao início e ao final da figura.
-Cada dígito é adicionado com seu vizinho à direita e o resultado é colocado abaixo do dígito correspondente da figura original.
-Se o resultado exceder nove, então a unidade é anotada e um ponto é colocado nela para lembrar que temos uma unidade que será adicionada na soma da próxima figura com seu vizinho à direita.
Exemplo detalhado de multiplicação por 11
Multiplique 673179 por 11
06731790 x 11 =
--
= 7404969
Os passos necessários para chegar a este resultado, ilustrado por cores, são os seguintes:
-O 1 da unidade do multiplicador (11) foi multiplicado pelo 9 do multiplicador (06731790) e foi adicionado 0. O dígito unitário do resultado foi obtido: 9.
-Em seguida, multiplicamos 1 por 7 e somamos nove a 16 e carregamos 1, colocamos os dez dígitos: 6.
-Depois de multiplicar 1 por 1, somar o vizinho à direita 7 mais 1 que ele carregava dá como resultado 9 para a centena.
-A próxima figura é obtida multiplicando 1 por 3 mais o vizinho 1, é 4 para o dígito dos milhares.
-Multiplique 1 por 7 e some o vizinho 3 resultando em 10, coloque o zero (0) como dez mil dígitos e leva um.
-Então, 1 vezes 6 mais o vizinho 7 resulta em 13 mais um 1 que teve os resultados 14, o 4 como cem mil dígitos e leva 1.
-Finalmente, 1 é multiplicado pelo zero que foi adicionado no início, dando zero mais o vizinho 6 mais um que foi carregado. Acontece que finalmente 7 para o dígito correspondente aos milhões.
- Multiplicação por números de 12 a 19
Para multiplicar qualquer número por 12:
-Um zero é adicionado no início e outro zero no final da figura a ser multiplicado.
-Cada dígito da figura a ser multiplicado é dobrado e adicionado com seu vizinho à direita.
-Se a soma for superior a 10, uma unidade é adicionada à próxima operação de duplicação e soma com o vizinho.
Exemplo de multiplicação por 12
Multiplique 63247 por 12
0632470 x 12 =
-
758964
Os detalhes para chegar a este resultado, seguindo estritamente as regras estabelecidas, são mostrados na figura a seguir:

- Extensão das regras de multiplicação por 13, ... até 19
O método de multiplicação por 12 pode ser estendido para a multiplicação por 13, 14 a 19 simplesmente mudando a regra de duplicação por triplicar para o caso de treze, quadruplicar para o caso de 14 e assim por diante até atingir 19.
Regras para produtos por 6, 7 e 5
- Multiplicação por 6
-Adicione zeros ao início e ao final da figura para multiplicar por 6.
-Adicione metade de seu vizinho à direita de cada dígito, mas se o dígito for ímpar, adicione 5 adicionais.
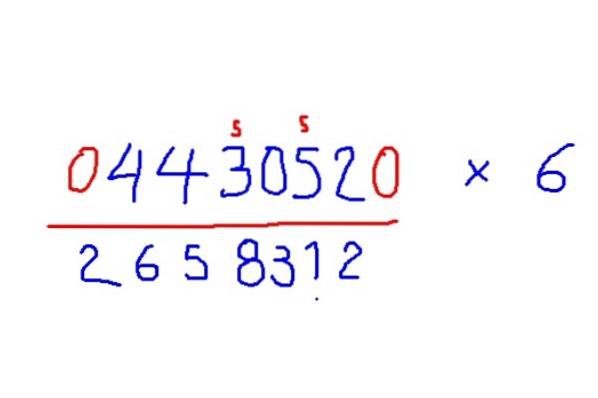
- Multiplicação por 7
-Adicione zeros ao início e ao final do número para multiplicar.
-Dobre cada dígito e adicione a metade inferior inteira do vizinho, mas se o dígito for ímpar, adicione 5.
Exemplo de multiplicação por 7
-Multiplique 3412 por 7
-O resultado é 23884. Para aplicar as regras, é recomendado primeiro reconhecer os dígitos ímpares e colocar um pequeno 5 acima deles para lembrar de adicionar este número ao resultado..
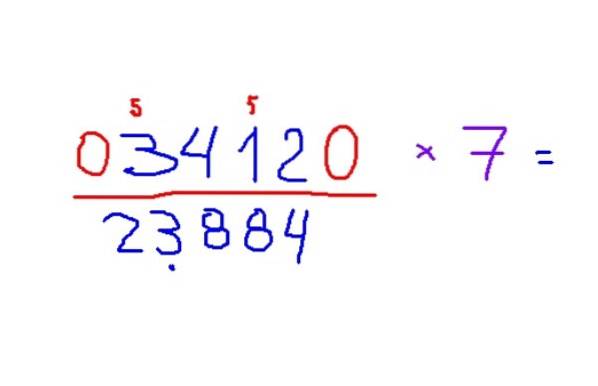
- Multiplicação por 5
-Adicione zeros ao início e ao final do número para multiplicar.
-Coloque sob cada dígito a metade inferior inteira do vizinho à direita, mas se o dígito for ímpar, adicione mais 5.
Exemplo multiplicação por 5
Multiplique 256413 por 5
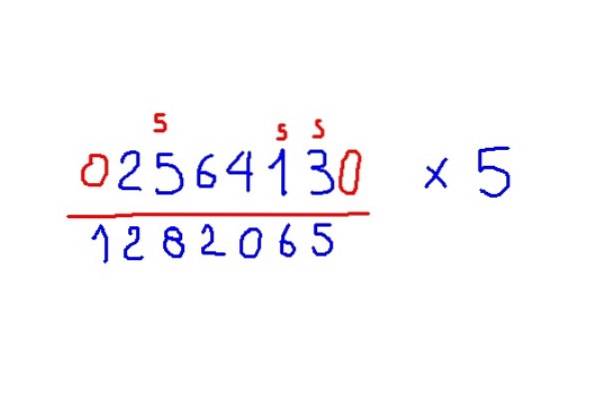
Regras para produtos por 9
-Um zero é adicionado no início e outro no final da figura para ser multiplicado por nove.
-O primeiro dígito à direita é obtido subtraindo o dígito correspondente do número para multiplicar de 10.
-Em seguida, o próximo dígito é subtraído de 9 e o vizinho é adicionado.
-O passo anterior é repetido até chegarmos ao zero do multiplicando, onde subtraímos 1 do vizinho e o resultado é copiado abaixo de zero..
Exemplo de multiplicação por 9
Multiplique 8769 por 9:
087690 x 9 =
--
78921
Operações
10 - 9 = 1
(9-6) + 9 = 1dois (a dois e leva 1)
(9-7) + 1 + 6 =9
(9-8) +7 =8
(8-1) = 7
Multiplicação por 8, 4, 3 e 2
-Adicione zeros ao início e ao final do número para multiplicar.
-Para o primeiro dígito da direita, subtraia de 10 e o resultado é duplicado.
-Para os seguintes dígitos subtraídos de 9, o resultado é duplicado e o vizinho é adicionado.
-Ao chegar a zero, subtraia 2 do vizinho à direita.
- Multiplicação por 8
Exemplo de multiplicação por 8
-Multiplique 789 por 8
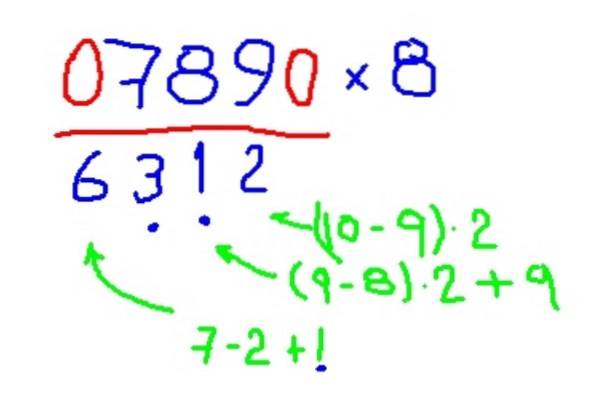
- Multiplicação por 4
-Adicione zeros à direita e à esquerda do multiplicando.
-Subtraia o dígito correspondente da unidade de 10 adicionando 5 se for um dígito ímpar.
-Subtraia cada dígito do multiplicando de 9 no formulário, adicionando metade do vizinho à direita e, se for um dígito ímpar, adicione 5 adicionalmente.
-Ao chegar ao zero do início do multiplicando, coloque metade do vizinho menos um.
Exemplo de multiplicação por 4
Multiplique 365187 x 4
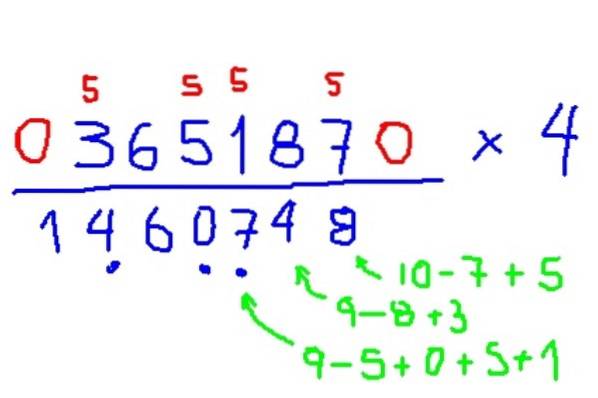
- Multiplicação por 3
-Adicione zero a cada extremidade do multiplicando.
-Subtraia 10 menos o dígito da unidade e adicione 5 se for um dígito ímpar.
-Para os outros dígitos, subtraia 9, dobre o resultado, some metade do vizinho e some 5 se for ímpar..
-Quando você atingir o zero do cabeçalho, coloque a metade inteira inferior do vizinho menos 2.
Exemplo de multiplicação por 3
Multiplique 2588 por 3

- Multiplicação por 2
-Adicione zeros nas extremidades e duplique cada dígito, se exceder 10 adicione um ao próximo.
Exemplo multiplicação por 2
Multiplique 2374 por 2
023740 x 2
04748
Multiplicar por figuras compostas
As regras listadas acima se aplicam, mas os resultados são executados à esquerda pelo número de casas correspondentes a dezenas, centenas e assim por diante. Vejamos o seguinte exemplo:
Exercício
Multiplique 37654 por 498
0376540 x 498
301232 régua para 8
338886 regra para 9
150616 régua para 4
18751692 soma final
Referências
- Cutler, Ann. 1960 O sistema de velocidade Trachtenberg de matemática básica. Doubleday e CO, NY.
- Dialnet. Sistema matemático básico rápido. Recuperado de: dialnet.com
- Canto matemático. Multiplicação rápida pelo método de Trachtenberg. Recuperado de: rinconmatematico.com
- The Trachtenberg Speed System of Basic Mathematics. Recuperado de: trachtenbergspeedmath.com
- Wikipedia. Método de Trachtenberg. Recuperado de: wikipedia.com



Ainda sem comentários