
Amostragem dupla


O que é amostragem dupla?
O amostragem dupla é uma técnica utilizada em estatística inferencial quando se deseja saber mais detalhes e certezas sobre uma determinada variável, que caracteriza uma determinada população.
A segunda amostra populacional é geralmente realizada após a coleta e análise de uma primeira amostra, cuja análise não produziu uma conclusão estatisticamente significativa em nenhuma das variáveis do estudo..
Por este motivo, a amostragem dupla nas estatísticas também é conhecida como amostragem de dois estágios. A utilidade da segunda amostra é que ajuda a determinar com maior precisão a estimativa de razões e regressões de uma determinada variável auxiliar, que surge à luz da análise de uma primeira amostra..
Outro uso que se dá à amostragem dupla é a coleta de informações para a realização de uma amostragem por estratos..
Exemplos
Várias situações em que a amostragem dupla é garantida serão descritas abaixo..
Controle de qualidade na produção de peças
O método de amostragem dupla é freqüentemente usado no controle de qualidade industrial e geralmente é feito em duas fases..
Por exemplo, suponha uma máquina industrial que fabrica certas peças. Por mais regulada que seja a máquina, nenhuma parte é idêntica à outra, pois podem ocorrer pequenas variações em suas dimensões e peso. Trata-se de determinar se um lote de peças fabricadas por essa máquina atende aos critérios de tolerância para sua aceitação ou rejeição..
Primeiro, é feita uma amostra aleatória de peças com a qual você deseja verificar se uma das variáveis, por exemplo, o comprimento da peça, está dentro da tolerância.
Caso o comprimento médio esteja abaixo ou acima do grau de tolerância desejado para a referida variável, nesta primeira amostra, infere-se que o lote está com defeito e deve ser descartado. Neste caso, nenhuma nova amostra é necessária.
Por outro lado, se o valor médio estiver dentro da faixa de tolerância, mas o desvio padrão da amostra for grande o suficiente para que a adição ou subtração do valor médio fique fora da faixa, uma segunda amostra maior precisará ser coletada..
Esta segunda amostra deve incluir a amostra original para refazer os cálculos e assim poder tomar uma decisão final sobre a variável investigada. Desta forma, pode-se saber se o lote está com defeito ou não.
Custos de amostragem mais baixos
Em muitas ocasiões, as informações sobre uma das variáveis a serem estudadas são de difícil acesso. Mas pode haver uma variável auxiliar mais facilmente para a coleta de dados.
Nesse caso, são tomadas duas amostras, uma grande para a variável auxiliar, menos cara, e uma amostra menor, contida na amostra maior da variável mais cara..
Este método é aplicável sempre que for determinado que existe uma correlação entre as duas variáveis, que geralmente é uma relação proporcional..
Um exemplo dessa situação aparece nas ciências florestais, onde se deseja determinar a porcentagem de árvores afetadas por uma planta parasita (micose)..
Por se tratar de regiões muito extensas e de difícil acesso, o estudo da população total de árvores não é viável a tempo e custos. Estas etapas são seguidas:
Etapa 1: coleta de amostras
Uma amostragem preliminar consistiria na utilização de fotografia aérea e a floresta é subdividida em lotes. A partir daqui alguns lotes são escolhidos aleatoriamente e estima-se, através da análise das imagens dos lotes escolhidos, quantas árvores são afetadas pela micose, uma vez que a cor das árvores é afetada pelo parasita..
Etapa 2: trabalho de campo
Mas a análise fotográfica pode ser imprecisa, então alguns lotes da primeira amostra são escolhidos, de preferência ao acaso, para fazer trabalho de campo..
Etapa 3: comparação
O resultado do campo é então comparado com o fotográfico para a interceptação dos dois conjuntos de lotes. Essa comparação pode ser realizada, por exemplo, fazendo-se um gráfico em que o eixo horizontal é o valor obtido para cada lote através da fotografia e no eixo vertical o valor obtido por lote através do trabalho de campo..
Este método gráfico permite identificar visualmente se existe ou não correlação entre os dois resultados e determinar, através de uma análise de regressão, o coeficiente de proporcionalidade ou razão entre as duas amostras..
Após a maior amostra, ou seja, a amostra fotográfica, obtém-se o valor médio das árvores infectadas e seu desvio padrão. Mas como o coeficiente de proporcionalidade e seu erro com as amostras de campo foram determinados, então é possível corrigir o resultado da amostra maior (a fotográfica).
Este resultado pode então ser extrapolado para toda a população de árvores.
Vantagens e desvantagens da amostragem dupla
Nos exemplos descritos, a vantagem de custo é evidente, pois a substituição de uma variável de fácil acesso por outra de difícil acesso economiza tempo e dinheiro..
Uma desvantagem é que, no caso de amostragem dupla para controle de qualidade, existe o risco de se passar por bons lotes de produtos fora da tolerância..
Exercício
Queremos estimar o número de árvores doentes em uma floresta de 162 hectares. Como a floresta é muito extensa, ela se subdivide em 100 parcelas da mesma área. 18 parcelas são escolhidas aleatoriamente e por meio de estudo fotográfico estima-se que nessas 18 parcelas existam 8,5 árvores doentes com um erro padrão de mais ou menos 4,5 árvores..
Destas 18 parcelas, 8 parcelas são escolhidas aleatoriamente nas quais o estudo de campo é realizado. Para essas oito parcelas, o estudo fotográfico mostra 10 árvores doentes com um erro de mais ou menos 5,3 árvores..
Por outro lado, para essas mesmas oito parcelas, o estudo de campo mostra 12,4 árvores doentes com um erro de mais menos 6,3 árvores..
Ele pergunta:
- a) Determine o coeficiente de proporcionalidade entre o estudo de campo por regressão linear.
- b) Estimar o número de árvores doentes pelo método fotográfico nas cem parcelas.
- c) Aplicar a correção com o coeficiente de proporcionalidade obtido, para estimar o número real de árvores doentes em toda a floresta.
Solução
É feito um gráfico do número de árvores por contagem fotográfica versus contagem de campo para os oito lotes selecionados para ambos os estudos..
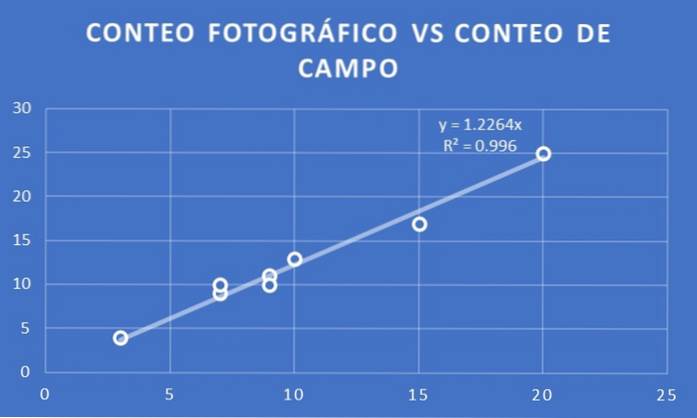
Uma linha de tendência é ajustada e sua inclinação determinada. Nesse caso, obtém-se que o coeficiente de proporcionalidade é de 1,23. Ou seja, se X for o número por contagem fotográfica, então estima-se que a contagem do campo será Y = 1,23 X.
O número de árvores doentes de acordo com a contagem fotográfica nos 18 lotes selecionados será:
18 x 8,5 = 153
Mas como toda a floresta foi dividida em 100 parcelas da mesma área, o número de árvores doentes estimado pelo método fotográfico é: (100/18) x 153 = 850.
O fator de correção obtido da comparação entre o estudo de campo e fotográfico é agora aplicado:
Número real estimado de árvores doentes na floresta = 1,23 x 850 = 1046.
Referências
- Amostragem dupla para estimativa de razão, PennState College. Recuperado de psu.edu
- Amostragem Dupla, Múltipla e Sequencial, NC State University. Recuperado de ncsu.edu
- Amostragem aleatória simples. Recuperado de investopedia.com
- O que é amostragem dupla? Recuperado de: nist.gov
- Amostragem. Recuperado de: en.wikipedia.org
- Amostragem em vários estágios. Recuperado de: en.wikipedia.org
Ainda sem comentários