
Ângulo inscrito de uma definição de círculo, teoremas, exemplos
O ângulo inscrito de um círculo É aquele que tem seu vértice na circunferência e seus raios são secantes ou tangentes a ele. Como consequência, o ângulo inscrito será sempre convexo ou plano..
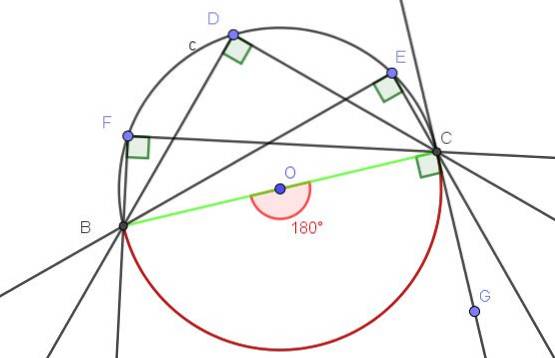
Na figura 1 estão representados vários ângulos inscritos em suas respectivas circunferências. O ângulo ∠EDF é inscrito por ter seu vértice D na circunferência e seus dois raios [DE) e [DF) interceptando a circunferência.
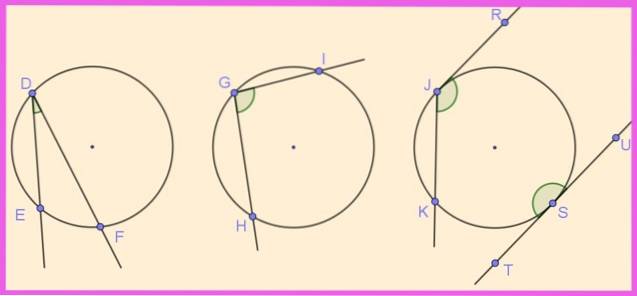
Da mesma forma, o ângulo ∠HGI é inscrito, pois tem seu vértice na circunferência e seus lados secantes a ele.
Os ângulos ∠KJR e ∠UST também estão inscritos na circunferência. O primeiro tem um lado secante e o outro tangente, enquanto o segundo tem seus dois lados tangentes à circunferência, formando um ângulo inscrito plano (180º).
Alguns autores chamam o ângulo de semi-inscrito que um de seus lados tem tangente à circunferência, mas neste artigo ele é considerado inscrito..
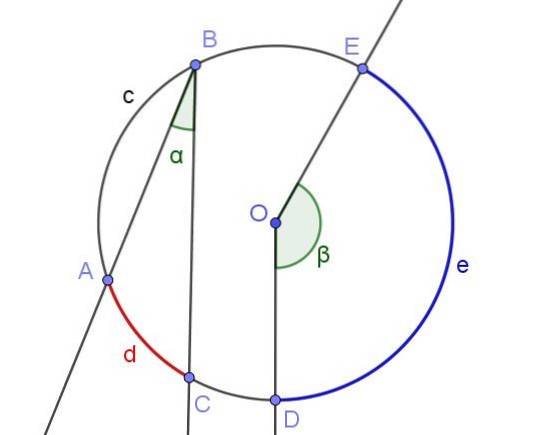
Cada ângulo inscrito define ou subtende um arco associado a ele. Por exemplo, na figura 2, o ângulo inscrito ∠ABC subtende o arco A⌒C de comprimento d.
A mesma figura mostra o ângulo ∠DOE, que não está inscrito na circunferência porque seu vértice não tem sua circunferência, mas sim no centro O.
Índice do artigo
- 1 ângulo central
- 2 teoremas
- 2.1 - Teorema 1 (ângulo inscrito e ângulo central)
- 2.2 - Teorema 2
- 2.3 - Teorema 3
- 3 exemplos
- 3.1 - Exemplo 1
- 3.2 - Exemplo 2
- 4 referências
Ângulo central
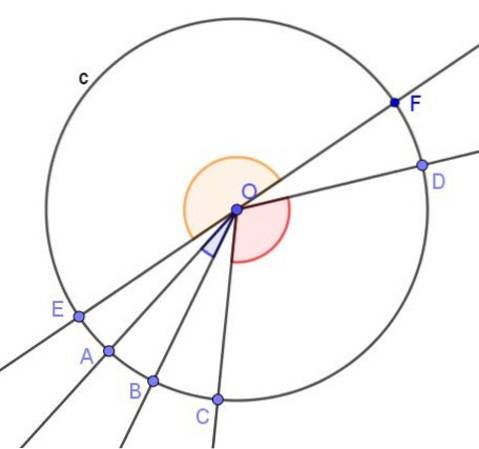
Além do ângulo inscrito, em uma circunferência o ângulo central, qual é aquele cujo vértice está no centro da circunferência e cujos lados cruzam a circunferência.
A medida em radianos de um ângulo central é o quociente entre o arco subtendente, ou seja, o arco de circunferência entre os lados do ângulo e o raio da circunferência.
Se a circunferência for unitária (de raio 1), então o comprimento do arco nas mesmas unidades de raio é a medida do ângulo em radianos.
E quando a medida do ângulo em graus é necessária, a medida em radianos é multiplicada pelo fator 180º / π.
Os instrumentos de medição de ângulo sempre usam um ângulo central e o comprimento do arco subtendido por ele é calibrado diretamente em graus. Isso significa que sempre que um ângulo é medido, no fundo o que é medido é o comprimento do arco subtendido pelo ângulo central.
Teoremas
- Teorema 1 (ângulo inscrito e ângulo central)
A medida de um ângulo inscrito é a metade da medida do ângulo central, se ambos os ângulos subtendem o mesmo arco.
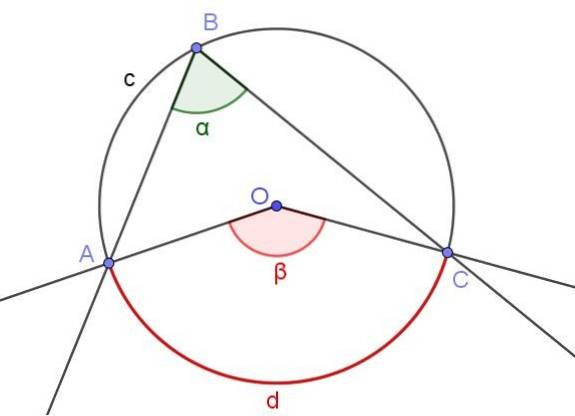
Na figura 4 são mostrados dois ângulos ∠ABC e ∠AOC, que interceptam o mesmo arco de circunferência A⌒C.
Se a medida do ângulo inscrito é α, então a medida β do ângulo central é duas vezes a medida do ângulo inscrito (β = 2 α) porque ambos subtendem o mesmo arco de medida d.
Demonstração 1a
Para provar o teorema 1, vamos começar mostrando vários casos particulares, até chegarmos ao caso geral.
Suponha um ângulo inscrito, no qual um de seus lados passe pelo centro da circunferência, conforme mostrado na figura 5.
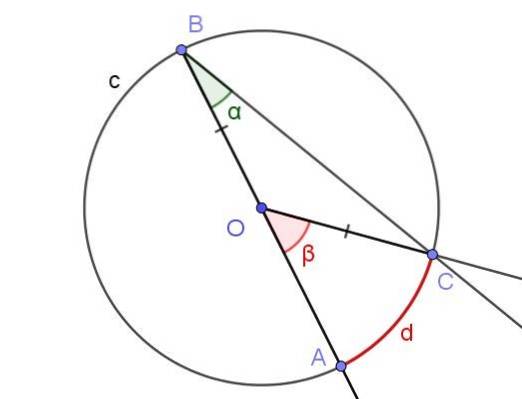
Neste caso, o triângulo isósceles COB é formado, uma vez que [OC] = [OB].
Em um triângulo isósceles, os ângulos adjacentes à base são iguais, portanto ∠BCO = ∠ABC = α. Por outro lado ∠COB = 180º - β.
Considerando a soma dos ângulos internos do triângulo COB, temos:
α + α + (180º - β) = 180º
Daí se segue que 2 α = β, ou o que é equivalente: α = β / 2. Isso coincide com o que afirma o teorema 1: a medida do ângulo inscrito é a metade do ângulo central, se ambos os ângulos subtendem o mesmo acorde [AC].
Demonstração 1b
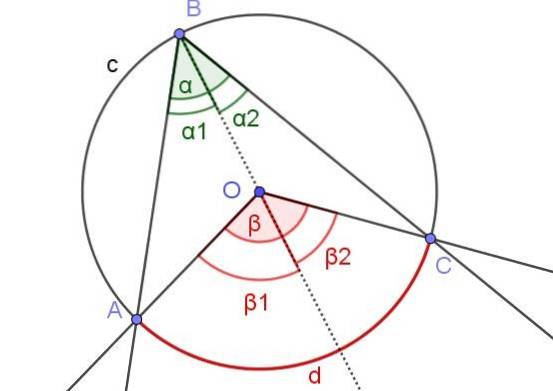
Neste caso, temos um ângulo inscrito ∠ABC, em que o centro O da circunferência está dentro do ângulo.
Para provar o Teorema 1 neste caso, o raio auxiliar [BO) é desenhado, de modo que temos dois ângulos inscritos ∠ABO e ∠OBC adjacentes ao referido raio.
Da mesma forma, temos os ângulos centrais β1 e βdois adjacente ao referido raio. Desta forma, temos a mesma situação da prova 1a, então pode-se afirmar que αdois = βdois / 2 e α1 = β1 /dois. Visto que α = α1 + αdois e β = β1 + βdois portanto, segue-se que α = α1 + αdois = β1 / 2 + βdois / 2 = (β1 + βdois) / 2 = β / 2.
Em conclusão α = β / 2, que cumpre o teorema 1.
- Teorema 2
Se dois ou mais ângulos inscritos subtendem o mesmo arco, eles têm a mesma medida.
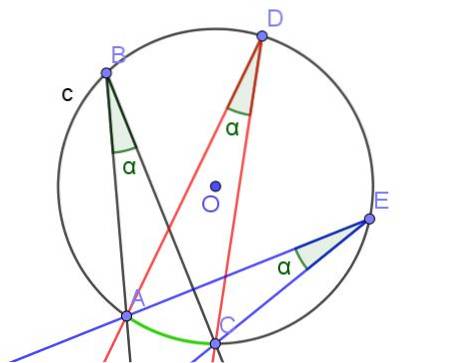
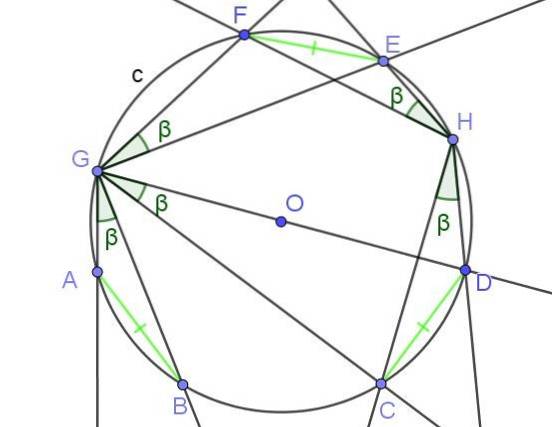
- Teorema 3
Os ângulos inscritos que subtendem acordes da mesma medida são iguais.
Exemplos
- Exemplo 1
Mostre que o ângulo inscrito que subtende o diâmetro é um ângulo reto.
Solução
O ângulo central ∠AOB associado ao diâmetro é um ângulo plano, cuja medida é 180º.
De acordo com o teorema 1, todo ângulo inscrito na circunferência que subtende a mesma corda (no caso o diâmetro), tem como medida a metade do ângulo central que subtende a mesma corda, que para o nosso exemplo é 180º / 2 = 90º.
- Exemplo 2
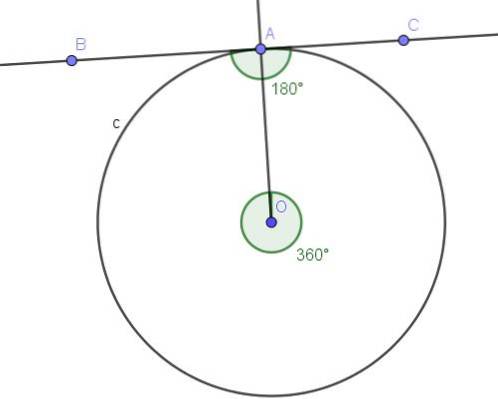
A linha (BC) tangente em A à circunferência C, determina o ângulo inscrito ∠BAC (ver figura 10).
Verifique se o teorema 1 dos ângulos inscritos é cumprido.
Solução
O ângulo ∠BAC é inscrito porque seu vértice está na circunferência, e seus lados [AB) e [AC) são tangentes à circunferência, então a definição do ângulo inscrito é satisfeita.
Por outro lado, o ângulo inscrito ∠BAC subtende o arco A, A, que é toda a circunferência. O ângulo central que subtende o arco A⌒A é um ângulo convexo cuja medida é o ângulo total (360º).
O ângulo inscrito que subtende todo o arco mede metade do ângulo central associado, ou seja, ∠BAC = 360º / 2 = 180º.
Com tudo o que foi dito acima, verifica-se que este caso particular cumpre o teorema 1.
Referências
- Baldor. (1973). Geometria e trigonometria. Editorial cultural da América Central.
- E. A. (2003). Elementos de geometria: com exercícios e geometria da bússola. Universidade de Medellin.
- Geometria 1º ESO. Ângulos na circunferência. Recuperado de: edu.xunta.es/
- All Science. Exercícios propostos de ângulos na circunferência. Recuperado de: francesphysics.blogspot.com
- Wikipedia. Ângulo inscrito. Recuperado de: es.wikipedia.com


Ainda sem comentários