
Definição e características do ângulo nulo, exemplos, exercícios
O ângulo nulo É aquele cuja medida é 0, tanto em graus como em radianos ou outro sistema de medição de ângulo. Portanto, falta largura ou abertura, como aquela formada entre duas linhas paralelas..
Embora sua definição pareça simples, o ângulo nulo é muito útil em muitas aplicações de física e engenharia, bem como em navegação e design..
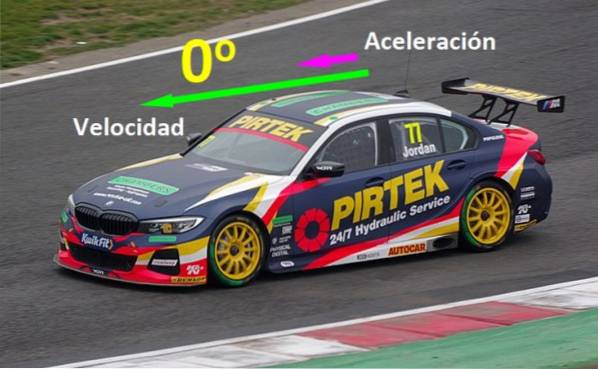
Existem quantidades físicas que devem ser alinhadas em paralelo para atingir certos efeitos: se um carro está se movendo em linha reta em uma rodovia e entra em seu vetor de velocidade v e seu vetor de aceleração para tem 0º, o carro anda cada vez mais rápido, mas se o carro freia, sua aceleração é oposta à sua velocidade (ver figura 1).
A figura a seguir mostra diferentes tipos de ângulo, incluindo o ângulo nulo à direita. Como pode ser visto, o ângulo 0º carece de largura ou abertura..

Índice do artigo
- 1 Exemplos de ângulos nulos
- 1.1 - Efeitos do ângulo nulo nas magnitudes físicas
- 2 exercícios
- 2.1 - Exercício 1
- 2.2 - Exercício 2
- 3 referências
Exemplos de ângulos nulos
As linhas paralelas são conhecidas por formarem um ângulo zero entre si. Quando você tem uma linha horizontal, ela é paralela ao eixo x do sistema de coordenadas cartesianas, portanto sua inclinação em relação a ela é 0. Em outras palavras, as linhas horizontais têm inclinação zero.
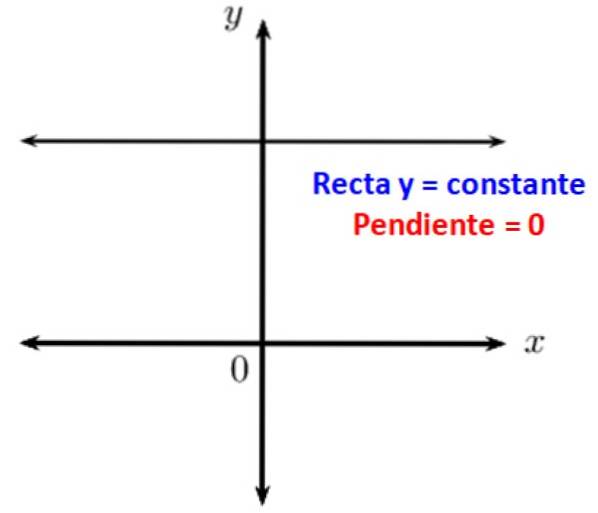
Além disso, as razões trigonométricas do ângulo nulo são 0, 1 ou infinito. Portanto, o ângulo nulo está presente em muitas situações físicas que envolvem operações com vetores. Esses motivos são:
-sen 0º = 0
-cos 0º = 1
-tg 0º = 0
-seg 0º = 1
-cosec 0º → ∞
-ctg 0º → ∞
E serão úteis para analisar alguns exemplos de situações em que a presença do ângulo nulo desempenha um papel fundamental:
- Efeitos do ângulo nulo nas quantidades físicas
Adição de vetor
Quando dois vetores são paralelos, o ângulo entre eles é zero, como visto na Figura 4a acima. Neste caso, a soma de ambos é realizada colocando-se um após o outro e a magnitude do vetor de soma é a soma das magnitudes dos adendos (figura 4b).

Quando dois vetores são paralelos, o ângulo entre eles é zero, como visto na Figura 4a acima. Neste caso, a soma de ambos é realizada colocando-se um após o outro e a magnitude do vetor de soma é a soma das magnitudes dos adendos (figura 4b)
O torque ou torque
O torque ou torque causa a rotação de um corpo. Depende da magnitude da força aplicada e como ela é aplicada. Um exemplo muito representativo é a chave inglesa na figura.
Para obter o melhor efeito de giro, a força é aplicada perpendicular ao cabo da chave, para cima ou para baixo, mas nenhuma rotação é esperada se a força for paralela ao cabo..
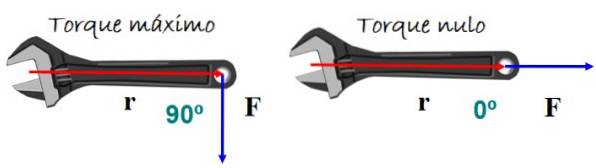
Torque matematicamente τ é definido como o produto vetorial ou produto cruzado entre vetores r (vetor de posição) e F (vetor de força) da figura 5:
τ = r x F
A magnitude do torque é:
τ = r F sin θ
Onde θ é o ângulo entre r Y F. Quando sen θ = 0 o torque é zero, neste caso θ = 0º (ou também 180º).
Fluxo de campo elétrico
O fluxo do campo elétrico é uma magnitude escalar que depende da intensidade do campo elétrico e também da orientação da superfície por onde passa..
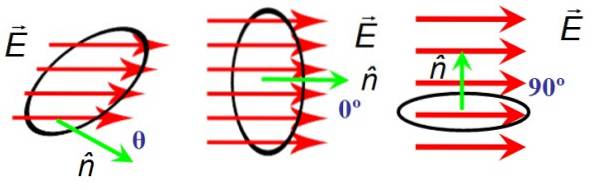
Na figura 6, há uma superfície circular da área A através da qual as linhas de campo elétrico passam E. A orientação da superfície é dada pelo vetor normal n. À esquerda, o campo e o vetor normal formam um ângulo agudo arbitrário θ, no centro eles formam um ângulo nulo entre si, e à direita eles são perpendiculares.
Quando E Y n são perpendiculares, as linhas de campo não cruzam a superfície e, portanto, o fluxo é zero, enquanto que quando o ângulo entre E Y n é nulo, as linhas atravessam completamente a superfície.
Denotando o fluxo do campo elétrico pela letra grega Φ (leia "fi"), sua definição para um campo uniforme como na figura, fica assim:
Φ = E•nPARA
O ponto no meio de ambos os vetores denota o produto escalar ou produto escalar, que é alternativamente definido como segue:
Φ = E•nA = EAcosθ
O negrito e as setas acima da letra são recursos para diferenciar entre um vetor e sua magnitude, que é denotada por letras normais. Uma vez que cos 0 = 1, o fluxo é máximo quando E Y n eles são paralelos.
Treinamento
- Exercício 1
Duas forças P Y Q atuam simultaneamente em um objeto de ponto X, ambas as forças inicialmente formam um ângulo θ entre elas. O que acontece com a magnitude da força resultante quando θ diminui para zero?
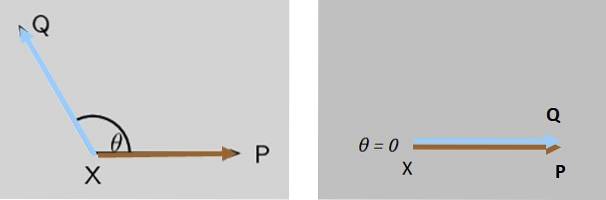
Solução
A magnitude da força resultante Q + P aumenta gradualmente até que esteja no máximo quando Q Y P são totalmente paralelos (figura 7 à direita).
- Exercício 2
Indique se o ângulo nulo é uma solução da seguinte equação trigonométrica:
cos 2x = 1 + 4 sen x
Solução
Uma equação trigonométrica é aquela em que o desconhecido é parte do argumento de uma razão trigonométrica. Para resolver a equação proposta, é conveniente usar a fórmula para o cosseno do ângulo duplo:
cos 2x = cosdois x - pecadodois x
Porque, desta forma, o argumento do lado esquerdo torna-se x em vez de 2x. Então:
porquedois x - pecadodois x = 1 + 4sin x
Por outro lado porquedois x + pecadodois x = 1, então:
porquedois x - pecadodois x = cosdois x + pecadodois x + 4sen x
O termo cosdois x é cancelado e permanece:
- sendois x = pecadodois x + 4sen x → - 2sendois x - 4senx = 0 → 2sendois x + 4senx = 0
Agora a seguinte mudança de variável é feita: sinx = u e a equação se torna:
2udois + 4u = 0
2u (u + 4) = 0
Cujas soluções são: u = 0 e u = -4. Retornando a mudança, teríamos duas possibilidades: sin x = 0 e sinx = -4. Esta última solução não é viável, porque o seno de qualquer ângulo está entre -1 e 1, então ficamos com a primeira alternativa:
sin x = 0
Portanto x = 0º é uma solução, mas qualquer ângulo cujo seno seja 0 também funciona, que também pode ser 180º (π radianos), 360º (2 π radianos) e os respectivos negativos também.
A solução mais geral da equação trigonométrica é: x = kπ onde k = 0, ± 1, ± 2, ± 3,…. k um inteiro.
Referências
- Baldor, A. 2004. Geometria plana e espacial com trigonometria. Publicaciones Cultural S.A. de C.V. México.
- Figueroa, D. (2005). Série: Física para Ciência e Engenharia. Volume 3. Sistemas de partículas. Editado por Douglas Figueroa (USB).
- Figueroa, D. (2005). Série: Física para Ciência e Engenharia. Volume 5. Interação elétrica. Editado por Douglas Figueroa (USB).
- OnlineMathLearning. Tipos de ângulos. Recuperado de: onlinemathlearning.com.
- Zill, D. 2012. Algebra, Trigonometry and Analytical Geometry. McGraw Hill Interamericana.


Ainda sem comentários