
Ângulos nos tipos de circunferência, propriedades, exercícios resolvidos
Chamam-se ângulos de circunferência aqueles em que alguns de seus elementos são ou se cruzam em uma determinada circunferência. Entre eles estão os seguintes:
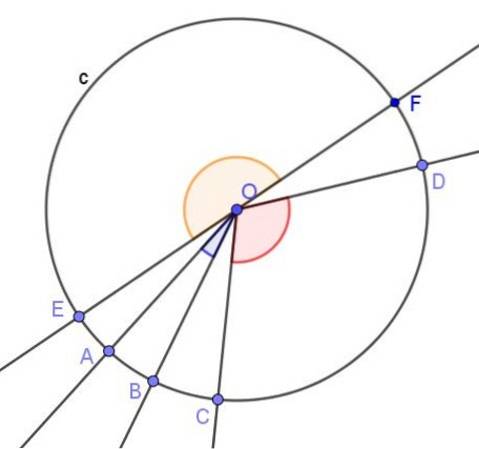
1.- O ângulo central, cujo vértice está no centro da circunferência e seus lados são secantes a ela, como podemos ver na imagem a seguir:

2.- O ângulo inscrito, cujo vértice está na circunferência e seus lados são secantes ou tangentes à circunferência.
3.- Ângulo externo, cujo vértice está fora da circunferência, mas seus lados são secantes ou tangentes à circunferência.
4.- O ângulo interior, com o vértice dentro da circunferência e seus lados secantes a ele.
Todos esses ângulos têm certas relações entre si e isso nos leva a propriedades importantes entre os ângulos pertencentes a um determinado círculo.
Índice do artigo
- 1 propriedades
- 1.1 - Ângulo central
- 1.2 - Ângulo inscrito
- 1.3 - Ângulo externo
- 1.4 - Ângulo interno
- 2 exercícios resolvidos
- 2.1 - Exercício 1
- 2.2 - Exercício 2
- 3 referências
Propriedades
- Ângulo central
O ângulo central é definido como aquele cujo vértice está no centro da circunferência e seus lados interceptam a circunferência.
A medida em radianos de um ângulo central é o quociente entre o arco subtendente, ou seja, o arco de circunferência entre os lados do ângulo e o raio da circunferência.
Se a circunferência for unitária, ou seja, de raio 1, então a medida do ângulo central é o comprimento do arco, que corresponde ao número de radianos.
Se você quiser a medida do ângulo central em graus, multiplique a medida em radianos pelo fator 180º / π.
Os instrumentos de medição do ângulo, como o transferidor e o goniômetro, sempre usam um ângulo central e o comprimento do arco subtendido.
Eles são calibrados em graus sexagesimais, o que significa que sempre que um ângulo é medido com eles, no fundo o que é medido é o comprimento do arco subtendido pelo ângulo central..
Propriedade
A medida de um ângulo central em radianos é igual ao comprimento do arco de subtensão ou interceptação dividido pelo comprimento do raio.
- Ângulo inscrito
O ângulo inscrito de um círculo é aquele que tem seu vértice na circunferência e seus raios são secantes ou tangentes a ele..
Suas propriedades são:
Propriedades
-O ângulo inscrito é convexo ou plano.
-Quando um ângulo inscrito cruza o mesmo arco que o ângulo central, a medida do primeiro ângulo será a metade da do segundo..
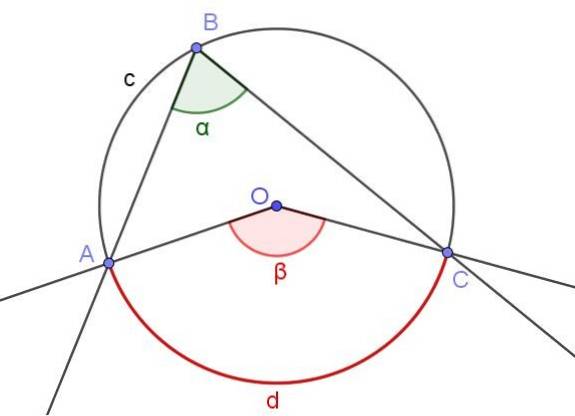
A Figura 3 mostra dois ângulos ∠ABC e ∠AOC que cruzam o mesmo arco de circunferência A⌒C.
Se a medida do ângulo inscrito é α, então a medida β do ângulo central é duas vezes a medida do ângulo inscrito (β = 2 α) porque ambos subtendem o mesmo arco de medida d.
- Ângulo externo
É o ângulo cujo vértice está fora da circunferência e cada um de seus lados corta a circunferência em um ou mais pontos.
Propriedade
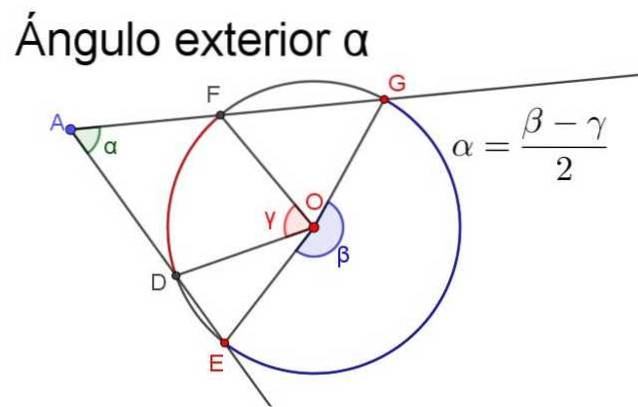
-Sua medida é igual à meia diferença (ou diferença dividida por 2) dos ângulos centrais que interceptam os mesmos arcos.
Para garantir que a medição seja positiva, a semidiferença deve ser sempre a do maior ângulo central menos a medida do menor ângulo central, conforme ilustrado na figura a seguir.
- Ângulo interno
O ângulo interno é aquele cujo vértice está dentro da circunferência e seus lados interceptam a circunferência.
Propriedade
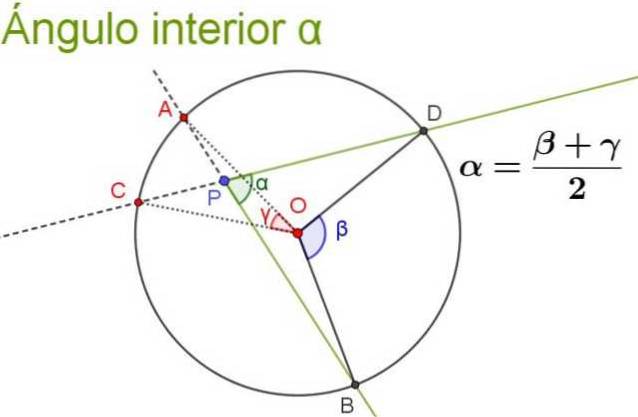
Sua medida é igual à semi-soma do ângulo central que subtende o mesmo arco, mais o ângulo central que subtende o mesmo arco que seu ângulo de extensão (este é o ângulo interno formado pelos raios complementares aos do ângulo interno original ).
A figura a seguir ilustra e esclarece a propriedade do ângulo interno.
Exercícios resolvidos
- Exercício 1
Suponha um ângulo inscrito no qual um de seus lados passe pelo centro do círculo, conforme mostrado na Figura 6. O raio do círculo é OA = 3 cm e o arco d tem um comprimento de π / 2 cm. Determine o valor dos ângulos α e β.
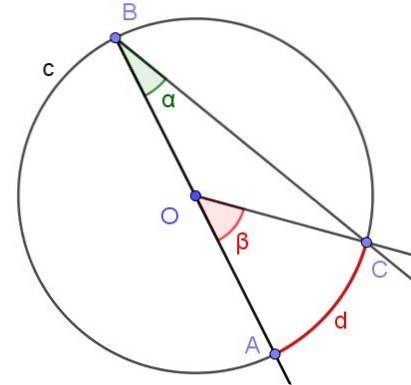
Solução
Nesse caso, forma-se o triângulo isósceles COB, pois [OC] = [OB]. Em um triângulo isósceles, os ângulos adjacentes à base são iguais, portanto ∠BCO = ∠ABC = α. Por outro lado ∠COB = 180º - β. Considerando a soma dos ângulos internos do triângulo COB, temos:
α + α + (180º - β) = 180º
Daí se segue que 2 α = β, ou o que é equivalente α = β / 2, com o que se confirma a propriedade (3) da seção anterior, que a medida do ângulo inscrito é a metade do ângulo central, quando ambos os ângulos subtenda o mesmo acorde [AC].
Agora passamos a determinar os valores numéricos: o ângulo β é central e sua medida em radianos é o quociente entre o arco d e o raio r = OA, então sua medida é:
β = d / r = (π / 2 cm) / (3 cm) = π / 6 rad = 30º.
Por outro lado, já havia sido afirmado que α = β / 2 = (π / 6 rad) / 2 = π / 12 rad = 15º.
- Exercício 2
Na figura 7 os ângulos α1 e βdois eles têm a mesma medida. Além disso, o ângulo β1 mede 60º. Determine os ângulos β e α.
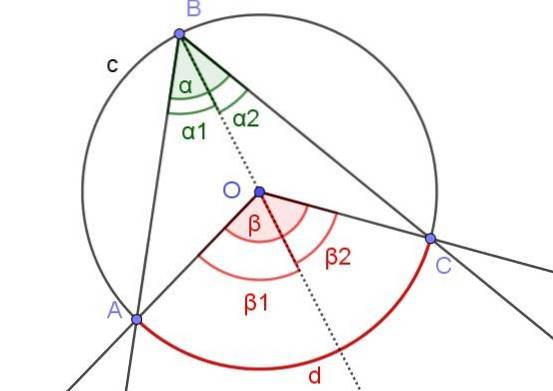
Solução
Neste caso, temos um ângulo inscrito ∠ABC em que o centro O da circunferência está dentro do ângulo.
Devido à propriedade (3) temos αdois = βdois / 2 e α1 = β1 /dois. O que:
α = α1 + αdois e β = β1 + βdois
Portanto, segue-se que:
α = α1 + αdois = β1 / 2 + βdois / 2 = (β1 + βdois) / 2 = β / 2.
Ou seja, de acordo com as propriedades:
α = β / 2
Uma vez que somos informados de que β1 = 60º então:
α1 = β1 / 2 = 60º / 2 = 30º.
Eles também nos dizem que α1 = βdois então segue-se que:
βdois = 30º.
O ângulo β resulta:
β1 + βdois = 60º + 30º = 90º.
E como α = β / 2, então:
α = 90º / 2 = 45º.
Em conclusão:
β = 90º e α = 45º.
Referências
- Baldor, A. 1973. Geometria e trigonometria. Editora Cultural da América Central.
- E. A. 2003. Elementos de geometria: com exercícios e geometria de compasso. Universidade de Medellin.
- Geometria 1º ESO. Ângulos na circunferência. Recuperado de: edu.xunta.es.
- All Science. Resolvidos problemas de ângulos na circunferência. Recuperado de: francesphysics.blogspot.com
- Wikipedia. Ângulo inscrito. Recuperado de: es.wikipedia.com



Ainda sem comentários