
Ângulos opostos ao vértice (com exercício resolvido)
O Ângulos opostos pelo vértice são aqueles que cumprem o seguinte: os lados de um deles são as extensões dos lados do outro ângulo. O teorema fundamental dos ângulos opostos pelo vértice diz assim: dois ângulos opostos pelo vértice têm a mesma medida.
Freqüentemente, a linguagem é abusada ao se dizer que os ângulos opostos ao vértice são iguais, o que não é correto. Só porque dois ângulos têm a mesma medida não significa que sejam iguais. É como dizer que duas crianças da mesma altura são iguais.
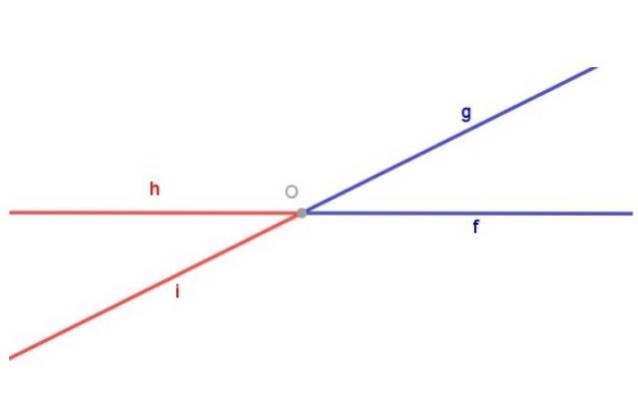
Lembre-se de que um ângulo é definido como a figura geométrica composta por dois raios com a mesma origem.
A Figura 1 mostra o ângulo névoa (azul) composto pelo raio [De) e o raio [Og) de origem comum OU. A Figura 1 também mostra o ângulo olá (vermelho) composto pelo raio [Ouvi) e o raio [Oh) ambos com origem OU.
Dois ângulos opostos pelo vértice são duas figuras geométricas diferentes. Para destacar isso, na figura 1 o ângulo foi colorido névoa azul, enquanto o ângulo olá foi colorido de vermelho.
Os ângulos azul e vermelho na Figura 1 são opostos no vértice porque: o raio [De) do ângulo azul é o prolongamento do raio [Oh) do ângulo vermelho e do raio [Og) do ângulo azul é o prolongamento do raio [Ouvi) do ângulo vermelho.
Índice do artigo
- 1 Conceitos importantes sobre ângulos
- 1.1 Lados e vértices de um ângulo
- 1.2 Ângulos formados por duas linhas que se cruzam
- 2 linhas perpendiculares e ângulo reto
- 2.1 Raios na mesma linha e ângulo plano
- 2.2 Ângulo nulo e ângulo total
- Medição de 3 ângulos
- 3.1 Sistema sexagesimal
- Teorema dos 4 ângulos do vértice
- 4.1 Demonstração
- 5 Exercício resolvido
- 5.1 Solução
- 6 referências
Conceitos importantes sobre ângulos
Lados e vértices de um ângulo
A figura geométrica que consiste em dois raios com origem comum é um ângulo. A imagem a seguir mostra o ângulo POQ formado pelos dois raios [OP) Y [OQ) de origem comum OU:
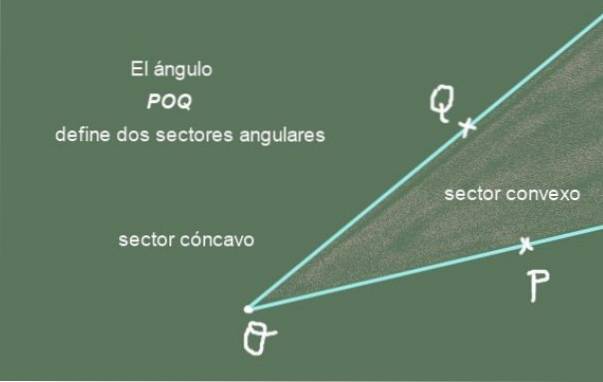
Os raios [OP) Y [OQ) são os lados angulares POQ, enquanto o ponto comum O é chamado vértice do ângulo.
Setor angular: Um ângulo divide o plano que o contém em dois setores angulares. Um deles é o setor angular convexo e o outro é o setor angular côncavo. A união dos dois setores dá o plano completo.
A Figura 2 mostra o ângulo POQ e seus dois setores angulares. O setor angular convexo é aquele com formato pontiagudo, enquanto o côncavo é o setor angular do plano que não possui o setor convexo..
Ângulos formados por duas linhas que se cruzam
Duas linhas de intersecção de um plano formam quatro ângulos e dividem o plano em quatro setores angulares.
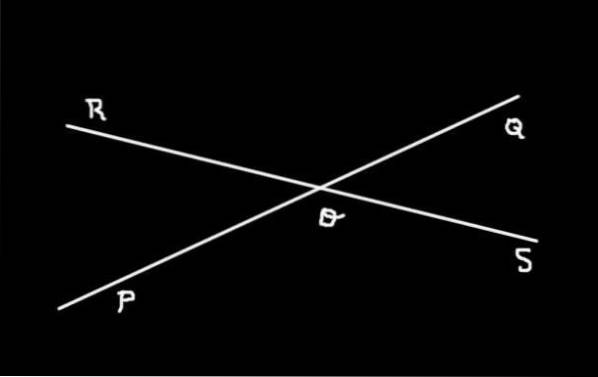
A Figura 3 mostra as duas linhas (PQ) Y (RS) que são interceptados em OU. Lá pode ser visto que quatro ângulos são determinados:
-SOQ, QOR, ROP Y POS
Os ângulos SOQ Y QOR, QOR Y ROP, ROP Y POS, POS Y SOQ Eles são ângulos adjacentes um ao outro, enquanto SOQ Y ROP eles são opostos no vértice. Eles também são Ângulos opostos pelo vértice Os ângulos QOR Y POS.
Linhas perpendiculares e ângulos retos
Duas linhas secantes (linhas que se cruzam) são Linhas retas perpendiculares se eles determinam quatro setores angulares de igual medida. Se cada um dos quatro setores for simétrico com o setor angular adjacente, eles terão a mesma medida.
Cada um dos ângulos que determinam as duas linhas perpendiculares é chamado ângulo reto. Todos os ângulos retos têm a mesma medida.
Raios na mesma linha e ângulo plano
Dada uma linha e um ponto nela, dois raios são definidos. Esses dois raios definem dois ângulos planos.
Na figura 3 você pode ver a linha (RS) e o ponto OU que pertence a (RS). O ângulo SOR é um ângulo plano. Também pode ser afirmado que o ângulo ROS é um ângulo plano. Todos os ângulos planos têm a mesma medida.
Ângulo nulo e ângulo total
Um único raio define dois ângulos: um deles o do setor angular convexo é o ângulo nulo e o outro, o do setor angular côncavo é o ângulo total. Na figura 3 você pode ver o ângulo nulo SOS e ele ângulo total SOS.
Medição de ângulo
Existem dois sistemas numéricos que são freqüentemente usados para dar a medida de um ângulo.
Um deles é o sistema sexagesimal, ou seja, baseado no número 60. É uma herança das antigas culturas mesopotâmicas. O outro sistema de medição de ângulos é o sistema de radianos, baseado no número π (pi) e é um legado dos antigos sábios gregos que desenvolveram a geometria.
Sistema sexagesimal
Ângulo nulo: no sistema sexagesimal o ângulo nulo mede 0º (zero graus).
Ângulo total: é atribuída a medida 360º (trezentos e sessenta graus).
Ângulo plano: no sistema sexagesimal o ângulo do plano mede 180º (cento e oitenta graus).
Ângulo reto: duas linhas perpendiculares dividem o plano em quatro ângulos de igual medida chamados ângulos retos. A medida de um ângulo reto é a quarta parte do ângulo completo, ou seja, 90º (noventa graus).
Transferidor ou goniômetro
O transferidor é o instrumento usado para medir ângulos. Consiste em um semicírculo (geralmente plástico transparente) dividido em 180 seções angulares. Visto que um semicírculo forma um ângulo plano, então a medida entre duas seções consecutivas é 1º.
O goniômetro é semelhante ao transferidor e consiste em um círculo dividido em 360 seções angulares.
Um ângulo cujos lados partem do centro do goniômetro cruzam dois setores e a medida desse ângulo em graus é igual ao número n de seções entre os dois setores interceptados, neste caso a medida será nº (lê-se “Graus de janeiro”).
Teorema dos ângulos do vértice
Formalmente, o teorema é afirmado desta forma:
Se dois ângulos são verticalmente opostos, eles têm a mesma medida.
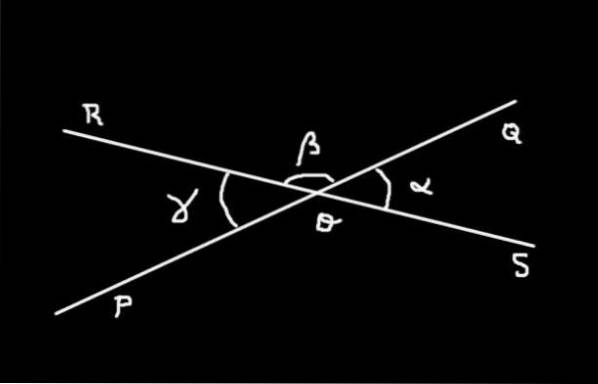
Demonstração
O ângulo SOQ tem medida α; o ângulo QOR tem medida β e ângulo ROP tem medida γ. A soma do ângulo SOQ mais ele QOR formar o ângulo do plano SOR medindo 180º.
Quer dizer que:
α + β = 180º
Por outro lado e usando o mesmo raciocínio com os ângulos QOR Y ROP se tem:
β + γ = 180º
Se observarmos as duas equações anteriores, a única maneira de ambas serem cumpridas é que α é igual a γ.
o que SOQ tem medida α e é oposto pelo vértice a ROP da medida γ, e como α = γ, conclui-se que os ângulos opostos ao vértice têm a mesma medida.
Exercício resolvido
Com referência à Figura 4: Suponha que β = 2 α. Encontre a medida dos ângulos SOQ, QOR Y ROP em graus sexagesimais.
Solução
Como a soma do ângulo SOQ mais ele QOR formar o ângulo do plano SOR se tem:
α + β = 180º
Mas eles nos dizem que β = 2 α. Substituindo este valor de β temos:
α + 2 α = 180º
Quer dizer:
3 α = 180º
O que significa que α é a terceira parte de 180º:
α = (180º / 3) = 60º
Então a medida de SOQ é α = 60º. A medida de QOR é β = 2 α = 2 * 60º = 120º. Finalmente gosto ROP é oposto por vértice a SOQ então, de acordo com o teorema já provado, eles têm a mesma medida. Ou seja, a medida de ROP é γ = α = 60º.
Referências
- Baldor, J. A. 1973. Plane and Space Geometry. Cultural da América Central.
- Leis e fórmulas matemáticas. Sistemas de medição de ângulo. Recuperado de: ingemecanica.com.
- Wikipedia. Ângulos opostos pelo vértice. Recuperado de: es.wikipedia.com
- Wikipedia. Esteira. Recuperado de: es.wikipedia.com
- Zapata F. Goniómetro: história, peças, operação. Recuperado de: lifeder.com


Ainda sem comentários