
Ângulos complementares o que são, cálculo, exemplos, exercícios
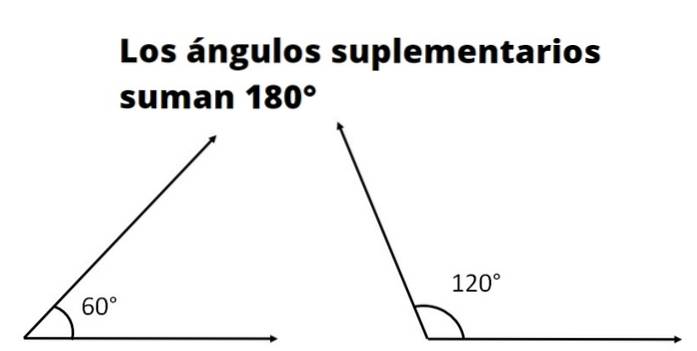
Dois ou mais são ângulos suplementares se a soma de suas medidas corresponde à medida de um ângulo reto. A medida de um ângulo reto, também chamado de ângulo plano, em graus é 180º e em radianos é π.
Por exemplo, descobrimos que os três ângulos internos de um triângulo são suplementares, já que a soma de suas medidas é 180º. Três ângulos são mostrados na Figura 1. Do exposto, segue-se que α e β são suplementares, uma vez que são adjacentes e sua soma completa um ângulo reto.
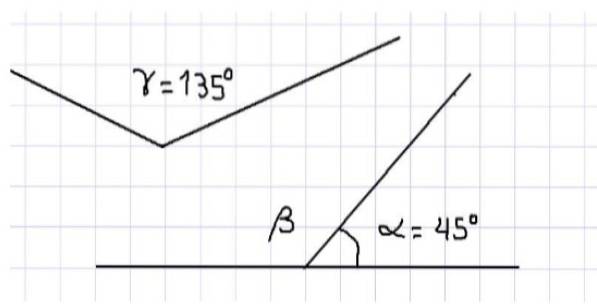
Ainda na mesma figura, temos os ângulos α e γ que também são complementares, pois a soma de suas medidas é igual à medida de um ângulo plano, ou seja, 180º. Não se pode dizer que os ângulos β e γ são complementares porque, como ambos os ângulos são obtusos, suas medidas são maiores que 90º e, portanto, sua soma excede 180º..
Por outro lado, pode-se afirmar que a medida do ângulo β é igual à medida do ângulo γ, pois se β é suplementar a α e γ é suplementar a α, então β = γ = 135º.
Índice do artigo
- 1 exemplos
- 1.1 Exemplo A
- 1.2 Exemplo B
- 1.3 Exemplo C
- 1.4 Exemplo D
- 1.5 Exemplo E
- 1.6 Exemplo F
- 2 exercícios
- 2.1 - Exercício I
- 2.2 - Exercício II
- 2.3 - Exercício III
- 3 ângulos suplementares em dois paralelos cortados por uma secante
- 3.1 - Exercício IV
- 4 referências
Exemplos
Nos exemplos a seguir, é solicitado encontrar os ângulos desconhecidos, indicados com pontos de interrogação na figura 2. Eles vão desde os exemplos mais simples até alguns um pouco mais elaborados que o leitor deve ser mais cuidadoso.
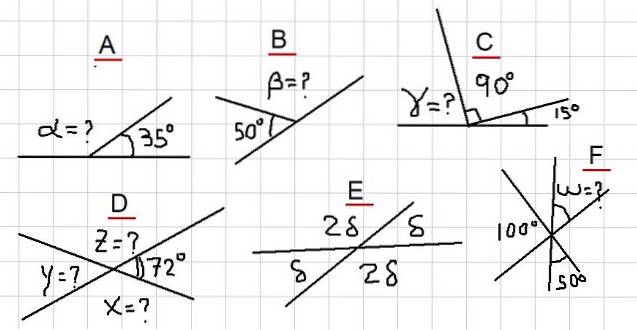
Exemplo A
Na figura temos que os ângulos adjacentes α e 35º somam um ângulo plano. Ou seja, α + 35º = 180º e, portanto, é verdade que: α = 180º- 35º = 145º.
Exemplo B
Uma vez que β é suplementar com o ângulo de 50º, segue-se que β = 180º - 50º = 130º.
Exemplo C
Da figura 2C observa-se a seguinte soma: γ + 90º + 15º = 180º. Ou seja, γ é suplementar com o ângulo 105º = 90º + 15º. Conclui-se então que:
γ = 180º- 105º = 75º
Exemplo D
Como X é suplementar a 72º, segue-se que X = 180º - 72º = 108º. Além disso, Y é suplementar com X, então Y = 180º - 108º = 72º.
E finalmente Z é suplementar com 72º, portanto Z = 180º - 72º = 108º.
Exemplo E
Os ângulos δ e 2δ são suplementares, portanto δ + 2δ = 180º. O que significa que 3δ = 180º, e isso por sua vez nos permite escrever: δ = 180º / 3 = 60º.
Exemplo F
Se chamarmos o ângulo entre 100º e 50º U, então U é suplementar a eles, pois se observa que sua soma completa um ângulo plano.
Segue imediatamente que U = 150º. Uma vez que U é oposto ao vértice de W, então W = U = 150º.
Treinamento
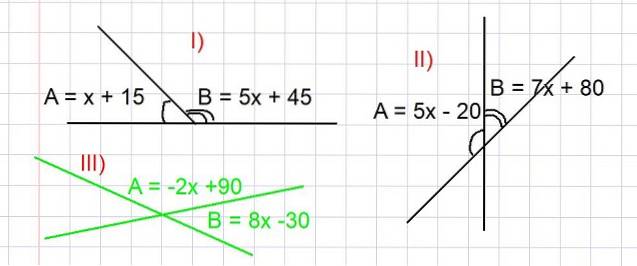
Três exercícios são propostos a seguir, em todos eles deve-se encontrar o valor dos ângulos A e B em graus, para que se cumpram as relações mostradas na figura 3. O conceito de ângulos suplementares é utilizado na resolução de todos eles..
- Exercício I
Determine os valores dos ângulos A e B da parte I) da Figura 3.
Solução
A e B são suplementares, dos quais temos que A + B = 180 graus, então a expressão de A e B é substituída em função de x, como aparece na imagem:
(x + 15) + (5x + 45) = 180
Uma equação linear de primeira ordem é obtida. Para resolver isso, os termos são agrupados imediatamente:
6 x + 60 = 180
Dividindo ambos os membros por 6, temos:
x + 10 = 30
E finalmente resolvendo, segue que x vale 20º.
Agora devemos inserir o valor de x para encontrar os ângulos solicitados. Portanto, o ângulo A é: A = 20 +15 = 35º.
E por sua vez, o ângulo B é B = 5 * 20 + 45 = 145º.
- Exercício II
Encontre os valores dos ângulos A e B da parte II) da Figura 3.
Solução
Como A e B são ângulos suplementares, temos que A + B = 180 graus. Substituindo a expressão de A e B em função de x dada na parte II) da figura 3, temos:
(-2x + 90) + (8x - 30) = 180
Mais uma vez, uma equação de primeiro grau é obtida, para a qual os termos devem ser convenientemente agrupados:
6 x + 60 = 180
Dividindo ambos os membros por 6, temos:
x + 10 = 30
Daí decorre que x vale 20º.
Em outras palavras, o ângulo A = -2 * 20 + 90 = 50º. Enquanto ângulo B = 8 * 20 - 30 = 130º.
- Exercício III
Determine os valores dos ângulos A e B da parte III) da figura 3 (na cor verde).
Solução
Como A e B são ângulos suplementares, temos que A + B = 180 graus. Devemos substituir A e B pela expressão como uma função de x dada na figura 3, da qual temos:
(5x - 20) + (7x + 80) = 180
12 x + 60 = 180
Dividindo ambos os membros por 12 para resolver o valor de x, temos:
x + 5 = 15
Finalmente, verifica-se que x vale 10 graus.
Agora procedemos à substituição para encontrar o ângulo A: A = 5 * 10 -20 = 30º. E para o ângulo B: B = 7 * 10 + 80 = 150º
Ângulos suplementares em dois paralelos cortados por uma secante
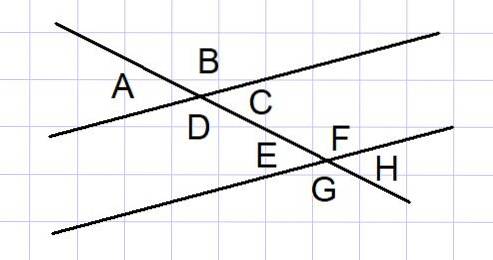
Duas linhas paralelas cortadas por uma secante é uma construção geométrica comum em alguns problemas. Entre essas linhas, 8 ângulos são formados como mostrado na figura 4.
Desses 8 ângulos, alguns pares de ângulos são complementares, que listamos a seguir:
- Os ângulos externos A e B e os ângulos externos G e H
- Os ângulos internos D e C, e os ângulos internos E e F
- Os ângulos externos A e G, e os ângulos externos B e H
- Os ângulos internos D e E, e os interiores C e F
Para completar, os ângulos iguais entre si também são nomeados:
- Os alternativos internos: D = F e C = E
- Os suplentes externos: A = H e B = G
- Os correspondentes: A = E e C = H
- Opostos pelo vértice A = C e E = H
- Os correspondentes: B = F e D = G
- Opostos pelo vértice B = D e F = G
- Exercício IV
Referindo-se à Figura 4, que mostra os ângulos entre duas linhas paralelas cortadas por uma secante, determine o valor de todos os ângulos em radianos, sabendo que o ângulo A = π / 6 radianos.
Solução
A e B são ângulos externos suplementares, então B = π - A = π - π / 6 = 5π / 6
A = E = C = H = π / 6
B = F = D = G = 5π / 6
Referências
- Baldor, J. A. 1973. Plane and Space Geometry. Cultural da América Central.
- Leis e fórmulas matemáticas. Sistemas de medição de ângulo. Recuperado de: ingemecanica.com.
- Wentworth, G. Plane Geometry. Recuperado de: gutenberg.org.
- Wikipedia. Ângulos suplementares. Recuperado de: es.wikipedia.com
- Wikipedia. Esteira. Recuperado de: es.wikipedia.com
- Zapata F. Goniómetro: história, peças, operação. Recuperado de: lifeder.com



Ainda sem comentários