
Número de Froude como é calculado e exemplos
O Número Froude em hidráulica indica a relação que existe entre as forças inerciais e as forças gravitacionais para um fluido. Portanto, é uma forma de designar o seguinte quociente:

OndeF é a notação para o número de Froude, uma quantidade adimensional que recebeu esse nome em homenagem ao notável arquiteto naval e engenheiro hidráulico britânico William Froude (1810-1879). Froude e seu filho experimentaram arrastar lençóis planos pela água para estimar a resistência dos barcos às ondas.

Na ação das ondas provocadas por um barco ao navegar ou pela corrente no pilar de uma ponte, as forças da inércia e da gravidade estão presentes.
O número de Froude é particularmente importante na caracterização do fluxo de fluido em um canal aberto. Um tubo ou canal aberto é um conduíte cuja superfície superior está aberta para a atmosfera. Os exemplos abundam na natureza, na forma de rios e riachos.
E nas construções feitas pelo homem temos:
-Calhas e ralos em ruas e edifícios para conduzir a água da chuva.
-Valas para irrigação.
-Aterros e drenos.
-Canais de resfriamento para maquinário industrial.
Todos esses são exemplos de tubos abertos para a atmosfera, nos quais o número de Froude deve ser sempre levado em consideração na caracterização do escoamento..
Índice do artigo
- 1 Cálculo do número de Froude
- 1.1 Número de Froude para um tubo aberto
- 2 Tipos de fluxo de acordo com o número de Froude
- 2.1 Número de Froude e número de Reynolds
- 3 exemplo trabalhado
- 3.1 Solução
- 4 referências
Cálculo do número de Froude
O quociente indicado no início, entre as forças de inércia e as da gravidade, assume a seguinte forma, dependendo dos parâmetros do fluido:
A equação anterior ou sua raiz quadrada é o número de Froude:

Número de Froude para um tubo aberto
Conforme explicado no início, o fluxo de água por canais abertos para a atmosfera é muito frequente. Para estes casos, o cálculo do número de Froude é realizado aplicando a seguinte fórmula:

NF = v / (gyh) ½
Onde Yh é a profundidade hidráulica, v é a velocidade média do fluxo e g é o valor da aceleração da gravidade. Por sua vez, a profundidade hidráulica é calculada da seguinte forma:
Yh = A / T
Nesta fórmula, A representa a área da seção transversal líquida e T é a largura da superfície livre do fluido, aquela que está exposta à atmosfera, no topo do canal ou tubo. É válido para um canal retangular ou largo o suficiente e com profundidade constante.
É importante destacar o fato de que, como a NF é adimensional, o produto Gyh deve ser o quadrado de uma velocidade. Na verdade, pode ser demonstrado que:
coudois = gyh
Com cou como a velocidade de propagação de uma onda de superfície, análoga à velocidade do som em um fluido. Portanto, o número de Froude também é análogo ao número de Mach, amplamente usado para comparar a velocidade dos aviões com a do som..
Tipos de fluxo de acordo com o número de Froude
O fluxo de fluido em um canal aberto é classificado em três regimes, de acordo com o valor de NF:
-Quando nF < 1, se tiene un movimiento en régimen lento o subcrítico.
-SemF = 1 o fluxo é nomeado fluxo crítico.
-Finalmente, se você tiver NF > 1 o movimento é realizado de forma rápida ou supercrítico.
Número Froude e número Reynolds
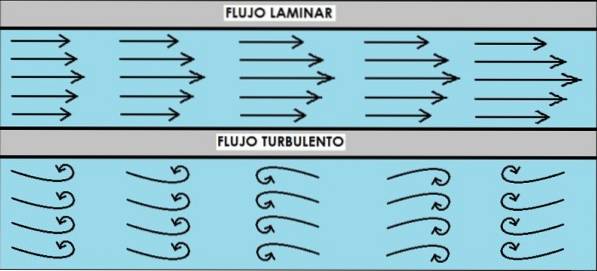
Reynolds número NR é outra grandeza adimensional muito importante na análise do escoamento do fluido, pelo qual se sabe quando o fluido tem comportamento laminado e quando é turbulento. Esses conceitos são aplicáveis aos fluxos de tubo fechado e canal aberto..
Um fluxo é laminar quando o fluido se move suave e ordenadamente em camadas que não se misturam. Por outro lado, o fluxo turbulento é caracterizado por ser caótico e desordenado.
Uma maneira de descobrir se um fluxo de água é laminar ou turbulento é injetando um jato de tinta. Se o fluxo for laminar, o fluxo de tinta flui separadamente daquele da água, mas se for um fluxo turbulento, a tinta se mistura e se dissipa na água rapidamente.

Nesse sentido, ao combinar os efeitos do número de Froude com os do número de Reynolds, temos:
-Laminar Subcrítico: NR < 500 y NF < 1
-Subcrítico turbulento: NR > 2000 e NF < 1
-Laminar Supercrítico: NR < 500 y NF > 1
-Turbulento supercrítico: NR > 2000 e NF > 1
Quando os fluxos ocorrem nas regiões de transição, é mais difícil caracterizá-los, devido à sua instabilidade.
Exemplo trabalhado
Um rio de 4 m de largura e 1 m de profundidade tem uma vazão de 3 m3 / s. Determine se o fluxo é subcrítico ou supercrítico.
Solução
Para encontrar o valor de NF é necessário saber a velocidade da corrente do rio. A declaração nos dá a taxa de fluxo, também conhecida como taxa de fluxo de volume, que depende da área da seção transversal e da velocidade v do fluxo. É calculado assim:
Q = A.v
Onde Q é o fluxo, PARA é a área da seção transversal ev é a velocidade. Supondo uma área de seção transversal retangular:
A = largura x profundidade = 4 m x 1 m = 4 mdois
Então, a velocidade v é:
v = Q / A = 3 m3 / s / 4 mdois= 0,75 m / s
A profundidade hidráulica no caso do tubo de seção retangular coincide com a profundidade, portanto, substituindo valores na equação por NF, com Yh = 1 m Y g = 9,8 m / sdois se tem:
NF = v / (gyh) ½ = 0,75 m / s / (9,8 m / sdois x 1m) ½ = 0,24
Desde NF for menor que 1, o fluxo tem um comportamento subcrítico, ou seja, lento.
Referências
- Cimbala, C. 2006. Mecânica dos Fluidos, Fundamentos e Aplicações. Mc. Colina Graw.
- Franzini, J. 1999. Mecânica dos Fluidos com Aplicação está na Engenharia. Mc. Colina Graw.
- Mott, R. 2006. Mecânica dos fluidos. 4º. Edição. Pearson Education.
- White, F. 2004. Fluid Mechanics. 5ª Edição. Mc Graw Hill.
- Wikipedia. Número Froude. Recuperado de: es.wikipedia.org.



Ainda sem comentários