O Número de Reynolds (Re) é uma quantidade numérica adimensional que estabelece a relação entre as forças inerciais e as forças viscosas de um fluido em movimento. As forças inerciais são determinadas pela segunda lei de Newton e são responsáveis pela aceleração máxima do fluido. Forças viscosas são as forças que se opõem ao movimento do fluido.
O número de Reynolds se aplica a qualquer tipo de fluxo de fluido, como fluxo em conduítes circulares ou não circulares, em canais abertos e fluxo em torno de corpos submersos..
O valor do número de Reynolds depende da densidade, da viscosidade, da velocidade do fluido e das dimensões do caminho da corrente. O comportamento de um fluido em função da quantidade de energia que é dissipada, devido ao atrito, vai depender se o fluxo é laminar, turbulento ou intermediário. Por este motivo é necessário encontrar uma forma de determinar o tipo de fluxo.
Uma maneira de determinar isso é por métodos experimentais, mas eles exigem muita precisão nas medições. Outra forma de determinar o tipo de fluxo é obtendo o número de Reynolds.
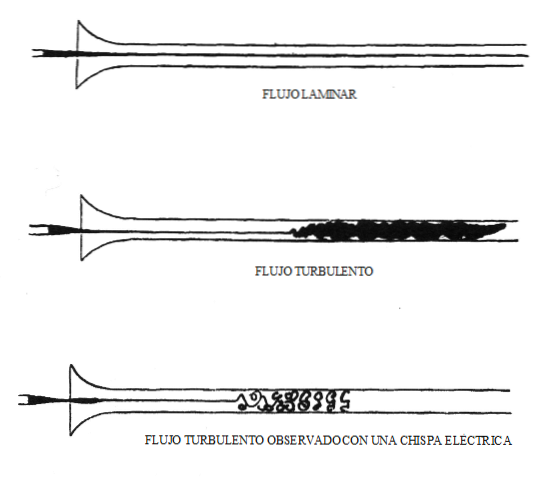
Em 1883, Osborne Reynolds descobriu que se o valor deste número adimensional for conhecido, o tipo de fluxo que caracteriza qualquer situação de condução de fluido pode ser previsto..
Índice do artigo
O número de Reynolds é usado para determinar o comportamento de um fluido, ou seja, para determinar se o fluxo de um fluido é laminar ou turbulento. O fluxo é laminar quando as forças viscosas, que se opõem ao movimento do fluido, são as que dominam e o fluido se move com velocidade suficientemente pequena e em percurso retilíneo.
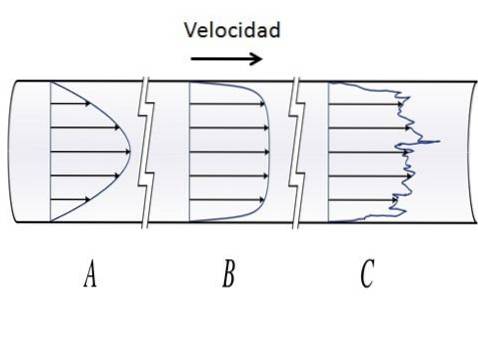
O fluido com fluxo laminar se comporta como se fossem infinitas camadas que deslizam umas sobre as outras, de maneira ordenada, sem se misturar. Em dutos circulares, o fluxo laminar tem um perfil de velocidade parabólico, com valores máximos no centro do duto e valores mínimos nas camadas próximas à superfície do duto. O valor do número de Reynolds no fluxo laminar é Re<2000.
O fluxo é turbulento quando as forças inerciais são dominantes e o fluido se move com mudanças flutuantes de velocidade e trajetórias irregulares. O fluxo turbulento é muito instável e exibe transferências de momentum entre as partículas de fluido.
Quando o fluido circula em um conduto circular, com fluxo turbulento, as camadas de fluido se cruzam formando redemoinhos e seu movimento tende a ser caótico. O valor do número de Reynolds para fluxo turbulento em um duto circular é Re > 4000.
A transição entre o fluxo laminar e o fluxo turbulento ocorre para valores numéricos de Reynolds entre 2000 Y 4000.
A equação usada para calcular o número de Reynolds em um duto de seção transversal circular é:
Re = ρVD / η
ρ = Densidade do fluido (kg / m3)
V = Velocidade do fluxo (m3/ s)
D = Dimensão linear característica do caminho do fluido, que para o caso do duto circular representa o diâmetro.
η = viscosidade dinâmica do fluido (Pa.s)
A relação entre viscosidade e densidade é definida como viscosidade cinemática v = η / ρ, e sua unidade é mdois/ s.
A equação do número de Reynolds em função da viscosidade cinemática é:
Re = VD / v
Em dutos e canais com seções transversais não circulares, a dimensão característica é conhecida como Diâmetro Hidráulico DH y representa uma dimensão generalizada do caminho do fluido.
A equação generalizada para calcular o número de Reynolds em conduítes com seções transversais não circulares é:
Re = ρV 'DH / η
V '= Velocidade média de fluxo =VAI
Diâmetro Hidráulico DH estabelece a relação entre a área PARA da seção transversal do fluxo de fluxo e perímetro molhado PM .
DH = 4A / PM
O perímetro molhado PM é a soma dos comprimentos das paredes do duto, ou canal, que estão em contato com o fluido.
Você também pode calcular o número de Reynolds de um fluido que envolve um objeto. Por exemplo, uma esfera imersa em um fluido se movendo com velocidade V. A esfera sofre uma força de arrasto FR definido pela equação de Stokes.
FR = 6πRVη
R = raio da esfera
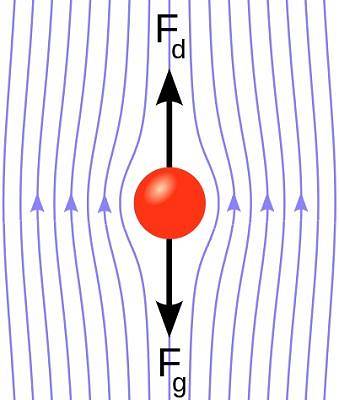
O número de Reynolds de uma esfera com velocidade V imerso em um fluido está:
Re = ρV R / η
Re<1 cuando el flujo es laminar y Re > 1 quando o fluxo é turbulento.
A seguir estão três exercícios de aplicação do número de Reynolds: conduíte circular, conduíte retangular e esfera imersa em um fluido.
Calcule o número de Reynolds de propilenoglicol a 20 °C em um duto circular de diâmetro 0,5 cm. A magnitude da velocidade do fluxo é 0,15m3/ s. Qual é o tipo de fluxo?
D =0,5 cm = 5,10-3m (dimensão característica)
A densidade do fluido é ρ = 1.036 g / cm3= 1036 kg / m3
Viscosidade do fluido é η = 0,042 Pa s = 0,042 kg / m.s
A velocidade do fluxo é V = 0,15m3/ s
A equação do número de Reynolds é usada em um duto circular.
Re =ρVOCÊS/η
Re = (1036 kg / m3x 0,15 m3/ s x 5,10-3m) /(0,042 kg / ms) = 18,5
O fluxo é laminar porque o valor do número de Reynolds é baixo em relação à relação Re<2000
Determine o tipo de fluxo do etanol que flui com velocidade de 25 ml / min em um tubo retangular. As dimensões da seção retangular são 0,5cm e 0,8cm.
Densidade ρ = 789 kg / m3
Viscosidade dinamica η = 1.074 mPa s = 1.074,10-3 kg / m.s
Primeiro determine a velocidade média do fluxo.
V ' =VAI
V = 25ml / min = 4.16,10-7m3/ s
A seção transversal é retangular cujos lados são 0,005m e 0,008m. A área da seção transversal é A = 0,005m x 0,008m = 4,10-5mdois
V ' = (4.16.10-7m3/ s) / (4,10-5mdois) = 1,04 × 10-doisem
O perímetro molhado é a soma dos lados do retângulo.
PM=0,013m
O diâmetro hidráulico é DH = 4A / PM
DH = 4 × 4,10-5mdois/ 0,013m
DH= 1.23.10-doism
O número de Reynolds é obtido a partir da equação Re = ρV 'DH / η
Re = (789 kg / m3x 1,04 × 10-doism / s x1.23.10-doism) / 1.074,10-3 kg / m.s
Re = 93974
O fluxo é turbulento porque o número de Reynolds é muito grande (Re> 2000)
Uma partícula esférica de poliestireno de látex cujo raio é R= 2000nm é jogado verticalmente na água com uma velocidade inicial de magnitude V0= 10 m / s. Determine o número de Reynolds da partícula imersa na água
Densidade de partículas ρ = 1,04 g / cm3 = 1040 kg / m3
R= 2000nm = 0,000002m
Densidade da água ρag= 1000 kg / m3
Viscosidade η =0,001 kg / (m s)
O número de Reynolds é obtido pela equação Re = ρV R / η
Re = (1000 kg / m3x10 m / s x 0,000002m) / 0,001 kg / (m s)
Re = 20
O número de Reynolds é 20. O fluxo é turbulento.
O número de Reynolds desempenha um papel importante na mecânica dos fluidos e na transferência de calor, pois é um dos principais parâmetros que caracterizam um fluido. Alguns de seus aplicativos são mencionados abaixo.
1-É usado para simular o movimento de organismos que se movem em superfícies líquidas, tais como: bactérias suspensas na água que nadam através do fluido e produzem agitação aleatória.
2-Tem aplicações práticas no escoamento de tubagens e em canais de circulação de líquidos, escoamentos confinados, nomeadamente em meios porosos.
3-Nas suspensões de partículas sólidas imersas em um fluido e em emulsões.
4-O número de Reynolds é aplicado em testes de túnel de vento para estudar as propriedades aerodinâmicas de várias superfícies, especialmente no caso de voos de aeronaves.
5-É usado para modelar o movimento de insetos no ar.
6-O projeto de reatores químicos requer a utilização do número de Reynolds para escolha do modelo de fluxo levando em consideração as perdas de carga, o consumo de energia e a área de transmissão de calor..
7-Na previsão da transferência de calor de componentes eletrônicos (1).
8-No processo de rega de jardins e pomares em que é necessário conhecer o fluxo da água que sai das tubagens. Para obter essa informação, é determinada a perda de carga hidráulica, que está relacionada ao atrito que existe entre a água e as paredes das tubulações. A queda de pressão é calculada assim que o número de Reynolds é obtido.
Em Biologia, o estudo do movimento de organismos vivos através da água, ou em fluidos com propriedades semelhantes às da água, requer a obtenção do número de Reynolds, que dependerá do tamanho dos organismos e da velocidade com que se deslocam..
Bactérias e organismos unicelulares têm um número de Reynolds muito baixo (Re<<1), consequentemente o escoamento tem perfil de velocidade laminar com predominância de forças viscosas.
Organismos com tamanho próximo ao das formigas (até 1cm) possuem um número de Reynolds da ordem de 1, que corresponde ao regime de transição em que as forças inerciais que atuam sobre o organismo são tão importantes quanto as forças viscosas do fluido.
Em organismos maiores, como as pessoas, o número de Reynolds é muito grande (Re>> 1).
Ainda sem comentários