
Propriedades de números complexos, exemplos, operações
O números complexos são o conjunto numérico que inclui os números reais e todas as raízes dos polinômios, incluindo as raízes pares dos números negativos. Essas raízes não existem no conjunto dos números reais, mas nos números complexos existe a solução.
Um número complexo consiste em uma parte real e uma parte chamada “imaginária”. A parte real é chamada para, por exemplo, e a parte imaginária ib, com para Y b números reais e "eu" gosto unidade imaginária. Desta forma, o número complexo assume a forma:
z = a + ib

Exemplos de números complexos são 2 - 3i, -πi, 1 + (1/2) i. Mas antes de operar com eles, vamos ver de onde se origina a unidade imaginária eu, considerando esta equação quadrática:
xdois - 10x + 34 = 0
Em que a = 1, b = -10 e c = 34.
Ao aplicar a fórmula de resolução para determinar a solução, encontramos o seguinte:

Como determinar o valor de √-36? Não há nenhum número real que resulta em uma quantidade negativa ao quadrado. Então conclui-se que esta equação não possui soluções reais.
No entanto, podemos escrever isso:
√-36 = √-6dois = √6dois (-1) = 6√-1
Se definirmos um certo valor x tal que:
xdois = -1
Então:
x = ± √-1
E a equação acima teria uma solução. Portanto, a unidade imaginária foi definida como:
i = √-1
E assim:
√-36 = 6i
Muitos matemáticos da antiguidade trabalharam na solução de problemas semelhantes, notadamente o Renascimento Girolamo Cardano (1501-1576), Nicolo Fontana (1501-1557) e Raffaele Bombelli (1526-1572).
Anos mais tarde, René Descartes (1596-1650) chamou quantidades como √-36 no exemplo de “imaginárias”. Por esta razão, √-1 é conhecido como o unidade imaginária.
Índice do artigo
- 1 Propriedades de números complexos
- 2 Representação de números complexos
- 2.1 - Forma binomial
- 2.2 - Forma polar
- 3 exemplos de números complexos
- 4 Para que eles servem?
- 5 operações com números complexos
- 5.1 - Exemplo 1
- 5.2 - Exemplo 2
- 6 aplicativo
- 7 referências
Propriedades de números complexos
-O conjunto de números complexos é denotado por C e inclui os números reais R e os números imaginários Im. Os conjuntos de números são representados em um diagrama de Venn, conforme mostrado na figura a seguir:
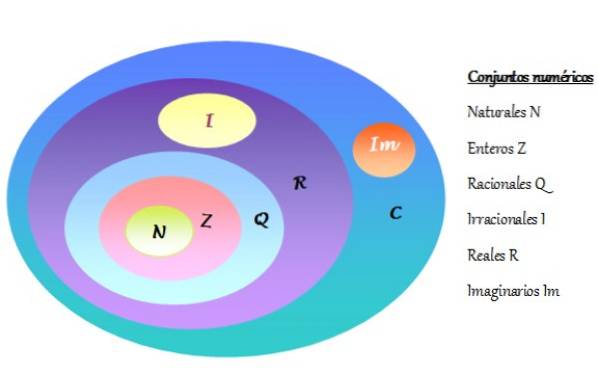
-Cada número complexo consiste em uma parte real e uma parte imaginária.
-Quando a parte imaginária de um número complexo é 0, é um número real puro.
-Se a parte real de um número complexo for 0, então o número é puramente imaginário.
-Dois números complexos são iguais se suas respectivas partes reais e imaginárias são iguais.
-Com os números complexos, as operações conhecidas de adição, subtração, multiplicação, produto e aprimoramento são realizadas, resultando em outro número complexo.
Representação de números complexos
Os números complexos podem ser representados de várias maneiras. Aqui estão os principais:
- Forma binomial
É a forma dada no início, onde z é o número complexo, para é a parte real, b é a parte imaginária e eu é a unidade imaginária:
z = a + ib
Ou também:
z = x + iy
Uma maneira de representar graficamente o número complexo é por meio do plano complexo mostrado nesta figura. O eixo imaginário Im é vertical, enquanto o eixo real é horizontal e é denotado como Re.
O número complexo z é representado neste plano como um ponto de coordenadas (x, y) ou (a, b), como é feito com os pontos do plano real.
A distância da origem ao ponto z é o módulo do número complexo, denotado como r, enquanto φ é o ângulo que forma r com o eixo real.
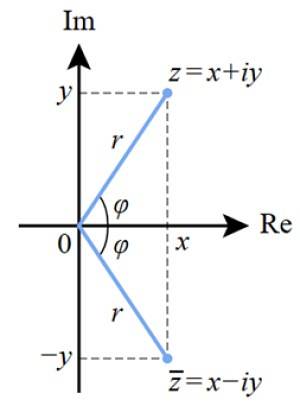
Esta representação está intimamente relacionada com a dos vetores no plano real. O valor de r corresponde a módulo do número complexo.
- Forma polar
A forma polar consiste em expressar o número complexo, dando os valores de r e de φ. Se olharmos para a figura, o valor de r corresponde à hipotenusa de um triângulo retângulo. As pernas valem para Y b, o bem x Y Y.
Da forma binomial ou binomial, podemos passar para a forma polar:
r = √xdois+Ydois
O ângulo φ É aquele que forma o segmento r com o eixo horizontal ou eixo imaginário. É conhecido como argumento do número complexo. Desta maneira:
φ = arctg (y / x)
O argumento tem valores infinitos, levando em consideração que cada vez que uma curva é virada, que vale 2π radianos, r ocupa a mesma posição novamente. Desta forma geral, o argumento de z, denotado Arg (z), é expresso assim:
Arg (z) = φ + 2kπ
Onde k é um número inteiro e é usado para indicar o número de voltas giradas: 2, 3, 4…. O sinal indica o sentido de rotação, se é no sentido horário ou anti-horário.
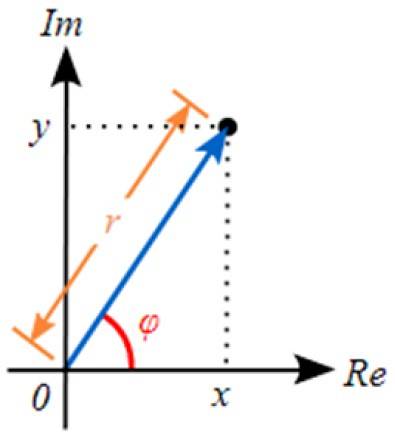
E se quisermos ir da forma polar para a forma binomial, usamos as razões trigonométricas. Na figura anterior, podemos ver que:
x = r cos φ
y = r sin φ
Desta forma, z = r (cos φ + i sen φ)
Que é abreviado assim:
z = r cis φ
Exemplos de números complexos
Os seguintes números complexos são fornecidos na forma binomial:
a) 3 + i
b) 4
d) -6i
E estes na forma de um par ordenado:
a) (-5, -3)
b) (0, 9)
c) (7,0)
Finalmente, este grupo é dado na forma polar ou trigonométrica:
a) √2 cis 45º
b) √3 cis 30º
c) 2 cis 315º
Para que servem?
A utilidade dos números complexos vai além da solução da equação quadrática apresentada no início, pois são essenciais no campo da engenharia e da física, especialmente em:
-O estudo das ondas eletromagnéticas
-Análise de corrente e tensão alternada
-Modelagem de todos os tipos de sinais
-Teoria da relatividade, onde o tempo é considerado uma magnitude imaginária.
Operações de número complexo
Com números complexos, podemos realizar todas as operações que são feitas com números reais. Alguns são mais fáceis de fazer se os números vierem na forma binomial, como adição e subtração. Em vez disso, a multiplicação e a divisão são mais simples se forem realizadas com a forma polar.
Vejamos alguns exemplos:
- Exemplo 1
Adicionar z1 = 2 + 5i e zdois = -3 -8i
Solução
As partes reais são adicionadas separadamente das partes imaginárias:
z1 + zdois = (2 + 5i) + (-3 -8i) = -1 -3i
- Exemplo 2
Multiplique z1 = 4 cis 45º e zdois = 5 cis 120º
Solução
Pode ser mostrado que o produto de dois números complexos na forma polar ou trigonométrica é dado por:
z1 . zdois = r1.rdois cis (φ1 + φdois)
De acordo com isso:
z1 . zdois = (4 × 5) cis (45 + 120) = 20 cis 165º
Aplicativo
Uma aplicação simples de números complexos é encontrar todas as raízes de uma equação polinomial como a mostrada no início do artigo.
No caso da equação xdois - 10x + 34 = 0, ao aplicar a fórmula de resolução obtemos:

Portanto, as soluções são:
x1 = 5 + 3i
xdois = 5 - 3i
Referências
- Earl, R. Complex numbers. Recuperado de: maths.ox.ac.uk.
- Figuera, J. 2000. Mathematics 1st. Diversificado. Edições CO-BO.
- Hoffmann, J. 2005. Seleção de tópicos de matemática. Publicações Monfort.
- Jiménez, R. 2008. Algebra. Prentice Hall.
- Wikipedia. Números complexos. Recuperado de: en.wikipedia.org



Ainda sem comentários