
Características de números compostos, exemplos, exercícios
O números compostos são aqueles inteiros que têm mais de dois divisores. Se olharmos de perto, todos os números são pelo menos divisíveis exatamente por eles mesmos e por 1. Aqueles que têm apenas esses dois divisores são chamados de primos, e aqueles que têm mais são compostos..
Vejamos o número 2, que só pode ser dividido entre 1 e 2. O número 3 também tem dois divisores: 1 e 3. Portanto, ambos são primos. Agora vamos olhar para o número 12, que podemos dividir exatamente por 2, 3, 4, 6 e 12. Por ter 5 divisores, 12 é um número composto.
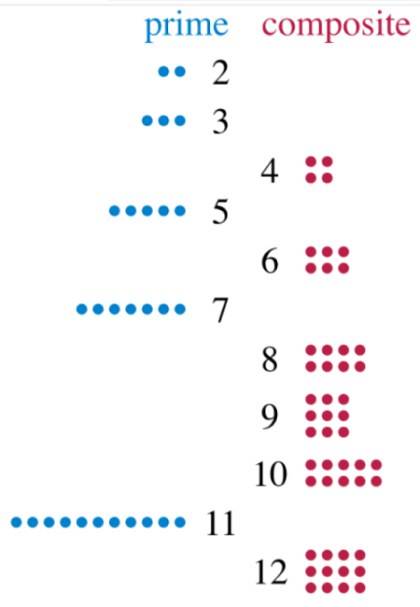
E o que acontece com o número 1, aquele que divide todos os outros? Bem, não é primo, porque não tem dois divisores, e não é composto, portanto, 1 não se enquadra em nenhuma dessas duas categorias. Mas há muitos, muitos outros números que o fazem..
Os números compostos podem ser expressos como o produto dos números primos, e esse produto, exceto pela ordem dos fatores, é único para cada número. Isso é assegurado pelo teorema fundamental da aritmética provado pelo matemático grego Euclides (325-365 aC).
Voltemos ao número 12, que podemos expressar de várias maneiras. Vamos tentar alguns:
12 = 4 x 3 = 2 x 6 = 12 x 1 = 2dois x 3 = 3 x 2dois = 3 x 2 x 2 = 2 x 2 x 3 = 2 x 3 x 2
As formas destacadas em negrito são produtos de números primos e a única coisa que muda é a ordem dos fatores, que sabemos não altera o produto. As outras formas, embora válidas para expressar 12, não consistem apenas em primos.
Exemplos de números compostos
Se quisermos decompor um número composto em seus fatores primos, devemos dividi-lo entre os números primos de forma que a divisão seja exata, ou seja, que o resto seja 0.
Este procedimento é chamado fatoração primária ou decomposição canônica. Fatores primários podem ser elevados a expoentes positivos.
Vamos decompor o número 570, observando que ele é par e, portanto, divisível por 2, que é um número primo.
Usaremos uma barra para separar o número à esquerda dos divisores à direita. Os respectivos quocientes são colocados sob o número à medida que são obtidos. A decomposição está completa quando a última figura na coluna da esquerda é 1:
570 │2
285 │
Ao dividir por 2, o quociente é 285, que é divisível por 5, outro número primo, terminando em 5.
570 │2
285 5
57 │
57 é divisível por 3, também um primo, pois a soma de seus dígitos 5 + 7 = 12 é um múltiplo de 3.
570 │2
285 5
57 3
19 │
Por fim, temos 19, que é um número primo, cujos divisores são 19 e 1:
570 │2
285 5
57 3
19-19
1 │
Ao obter 1, já podemos expressar 570 desta forma:
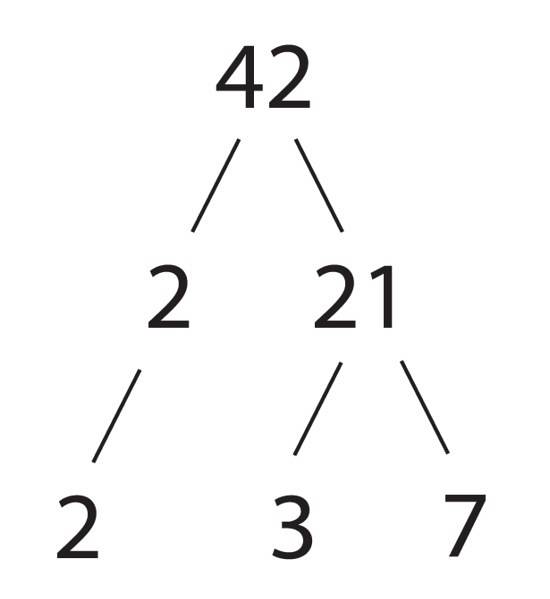
570 = 2 x 5 x 3 x 19
E vemos que, na prática, é o produto de 4 números primos.
Neste exemplo, começamos dividindo por 2, mas os mesmos fatores (em outra ordem) teriam sido obtidos se começássemos dividindo por 5, por exemplo.
Critérios de divisibilidade
Para decompor um número composto em seus fatores primos, é necessário dividi-lo exatamente. Os critérios de divisibilidade entre os números primos são regras que permitem saber quando um número é divisível por outro exatamente, sem ter que tentar ou provar.
-Divisibilidade por 2
Todos os números pares, aqueles que terminam em 0 ou um número par são divisíveis por 2.
-Divisibilidade por 3
Se a soma dos dígitos de um número for múltiplo de 3, o número também será divisível por 3.
-Divisibilidade por 5
Os números que terminam em 0 ou 5 são divisíveis por 5.
-Divisibilidade por 7
Um número é divisível por 7 se ao separar o último dígito, multiplicar por 2 e subtrair o número restante, o valor resultante for um múltiplo de 7.
Esta regra parece um pouco mais complicada do que as anteriores, mas na realidade não é muito, então vejamos um exemplo: 98 será divisível por 7?
Vamos seguir as instruções: separamos o último algarismo que é 8, multiplicamos por 2 que dá 16. O número que resta ao separar o 8 é 9. Subtraímos 16 - 9 = 7. E como 7 é um múltiplo de si mesmo , 98 é divisível entre 7.
-Divisibilidade por 11
Se a soma das figuras na posição par (2, 4, 6 ...) for subtraída da soma das figuras na posição ímpar (1, 3, 5, 7 ...) e 0 ou um múltiplo de 11 for obtido, o número é divisível por 11.
Os primeiros múltiplos de 11 são facilmente identificados: são 11, 22, 33, 44 ... 99. Mas tome cuidado, 111 não é, em vez disso 110 é.
Como exemplo, vamos ver se 143 é um múltiplo de 11.
Este número tem 3 dígitos, o único dígito par é 4 (o segundo), os dois dígitos ímpares são 1 e 3 (primeiro e terceiro), e sua soma é 4.
Ambas as somas são subtraídas: 4 - 4 = 0 e como 0 é obtido, verifica-se que 143 é um múltiplo de 11.
-Divisibilidade por 13
O número sem o dígito da unidade deve ser subtraído de 9 vezes esse dígito. Se a contagem retornar 0 ou um múltiplo de 13, o número é um múltiplo de 13.
Como exemplo, verificaremos que 156 é um múltiplo de 13. O dígito da unidade é 6 e o número que permanece sem ele é 15. Multiplicamos 6 x 9 = 54 e agora subtraímos 54 - 15 = 39.
Mas 39 é 3 x 13, então 56 é um múltiplo de 13.
Números primos entre si
Dois ou mais números primos ou compostos podem ser primos ou co-primos. Isso significa que o único divisor comum que eles têm é 1.
Existem duas propriedades importantes a serem lembradas quando se trata de coprimes:
-Dois, três e mais números consecutivos são sempre primos entre si.
-O mesmo pode ser dito para dois, três ou mais números ímpares consecutivos.
Por exemplo, 15, 16 e 17 são números primos entre si e, portanto, são 15, 17 e 19.
Como saber quantos divisores um número composto tem
Um número primo tem dois divisores, o mesmo número e 1. E quantos divisores um número composto tem? Estes podem ser primos ou compostos.
Seja N um número composto expresso em termos de sua decomposição canônica da seguinte forma:
N = an . bm. cp... rk
Onde a, b, c… r são os fatores primos en, m, p… k os respectivos expoentes. Bem, o número de divisores C que N tem é dado por:
C = (n +1) (m + 1) (p +1) ... (k + 1)
Com C = divisores principais + divisores compostos + 1
Por exemplo 570, que é expresso assim:
570 = 2 x 5 x 3 x 19
Todos os fatores primos são elevados a 1, portanto 570 tem:
C = (1 + 1) (1 + 1) (1+ 1) (1 +1) = 16 divisores
Destes 10 divisores já sabemos: 1, 2, 3, 5, 19 e 570. Existem mais 10 divisores ausentes, que são números compostos: 6, 10, 15, 30, 38, 57, 95, 114, 190 e 285. Eles são encontrados observando a decomposição em fatores primos e também multiplicando as combinações desses fatores..
Exercícios resolvidos
- Exercício 1
Decomponha os seguintes números em fatores primos:
a) 98
b) 143
c) 540
d) 3705
Solução para
98 │2
49 │7
7 │7
1 │
98 = 2 x 7 x 7
Solução b
143 11
13-13
1 │
143 = 11 x 13
Solução c
540 │5
108 │2
54 │2
27 │3
9 │3
3 │3
1 │
540 = 5 x 2 x 2 x 3 x 3 x 3 = 5 x 2dois x 33
Solução d
3705 5
741 │3
247 13
19-19
1 │
3705 = 5 x 3 x 13 x 19
- Exercício 2
Descubra se os seguintes números são primos entre si:
6, 14, 9
Solução
-Os divisores de 6 são: 1, 2, 3, 6
-Já o 14 é divisível por: 1, 2, 7, 14
-Finalmente, 9 tem como divisores: 1, 3, 9
O único divisor que eles têm em comum é 1, portanto, eles são primos um do outro.
Referências
- Baldor, A. 1986. Arithmetic. Edições e distribuições do Codex.
- Byju's. Números primos e compostos. Recuperado de: byjus.com.
- Números primos e compostos. Recuperado de: profeyennyvivaslapresentacion.files.wordpress.com
- Smartick. Critérios de divisibilidade. Recuperado de: smartick.es.
- Wikipedia. Números compostos. Recuperado de: en.wikipedia.org.



Ainda sem comentários