
Números quânticos, para que servem e para que servem

O nNúmeros quânticos são usados para descrever o estado quântico dos elétrons no átomo e se originam da solução da equação de Schrödinger para o mais simples de todos: hidrogênio.
A equação de Schrödinger é uma equação diferencial, cujas soluções são funções de onda e são denotados pela letra grega ψ. Soluções infinitas podem ser propostas, e seu quadrado é igual à probabilidade de encontrar o elétron em uma pequena região do espaço, chamada orbital.
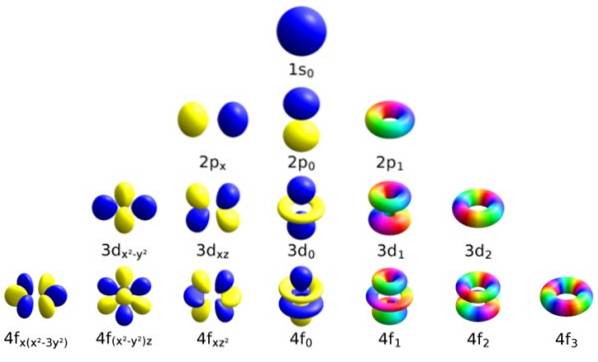
Cada orbital possui características definidas que o distinguem dos demais, como energia, momento angular e spin, propriedade inteiramente quântica do elétron e que é responsável, entre outras coisas, pelos efeitos magnéticos..
A maneira de identificar cada orbital é distingui-lo por um conjunto de números que o descrevem, e estes são precisamente os números quânticos:
-n: é o número quântico principal.
-ℓ: o número quântico azimutal.
-mℓ, é o número magnético.
-ms, o número do giro.
Índice do artigo
- 1 Para que servem os números quânticos?
- 1.1 Funções de onda
- 2 O que são números quânticos?
- 2.1 Número quântico principal
- 2.2 Número quântico do momento angular ou azimutal
- 2.3 Número quântico magnético mℓ
- 2.4 Número quântico de spin ms
- 3 referências
Para que servem os números quânticos?
Os números quânticos são usados para descrever o estado dos elétrons dentro do átomo. Esse modelo atômico em que o elétron gira em torno do núcleo é impreciso, porque não é consistente com a estabilidade atômica ou com um grande número de fenômenos físicos observados.
É por isso que o dinamarquês Niels Bohr (1885-1962) fez uma proposta audaciosa em 1913: o elétron só pode ser encontrado em certas órbitas estáveis, cujo tamanho depende de um inteiro chamado n.
Posteriormente, em 1925, o também físico austríaco Erwin Schrödinger (1887-1961) propôs uma equação diferencial em derivadas parciais, cujas soluções descrevem o átomo de hidrogênio. São as funções de onda ψ mencionadas no início.
Esta equação diferencial inclui as três coordenadas espaciais mais o tempo, mas quando isso não está incluído, a solução da equação de Schrödinger é análoga à de uma onda estacionária (uma onda que se propaga entre certos limites).
Funções de onda
A equação de Schrödinger independente do tempo é resolvida em coordenadas esféricas e a solução é escrita como o produto de três funções, uma para cada variável espacial. Neste sistema de coordenadas, em vez de usar as coordenadas dos eixos cartesianos x, Y Y z as coordenadas são usadas r, θ Y φ. Desta maneira:
ψ (r, θ, φ) = R (r) ⋅f (θ) ⋅g (φ)
A função de onda é intangível, no entanto a mecânica quântica nos diz que a amplitude ao quadrado:
| ψ (r, θ, φ) |dois
Ou seja, o módulo ou valor absoluto da função de onda, ao quadrado, é um número real que representa a probabilidade de encontrar o elétron, em uma determinada região ao redor do ponto cujas coordenadas são r, θ Y φ.
E esse fato é algo mais concreto e tangível.
Para encontrar a função de onda, você deve resolver três equações diferenciais ordinárias, uma para cada variável r, θ Y φ.
As soluções de cada equação, que serão as funções R (r), f (θ) eg (φ), contêm os três primeiros números quânticos mencionados.
O que são números quânticos?
Descrevemos brevemente a natureza de cada número quântico abaixo. Os três primeiros, como afirmado anteriormente, surgem das soluções da equação de Schrödinger.
A quarta edição foi adicionada por Paul Dirac (1902 - 1984) em 1928.
Número quântico principal
É denotado por n e indica o tamanho do orbital permitido, bem como a energia do elétron. Quanto maior o seu valor, mais longe o elétron está do núcleo e sua energia será maior também, mas em troca ele reduz sua estabilidade.
Este número surge da função R (r), que é a probabilidade de encontrar o elétron a uma certa distância r do núcleo, que é determinado por:
-Constante de Planck: h = 6,626 × 10 -3. 4 J.s
-Massa do elétron me = 9,1 × 10-31 kg
-Carga de elétron: e = 1,6 × 10-19 C.
-Constante eletrostática: k = 9 × 10 9 N.mdois/ Cdois
Quando n = 1 corresponde ao raio de Bohr que é de aproximadamente 5,3 × 10-11 m.
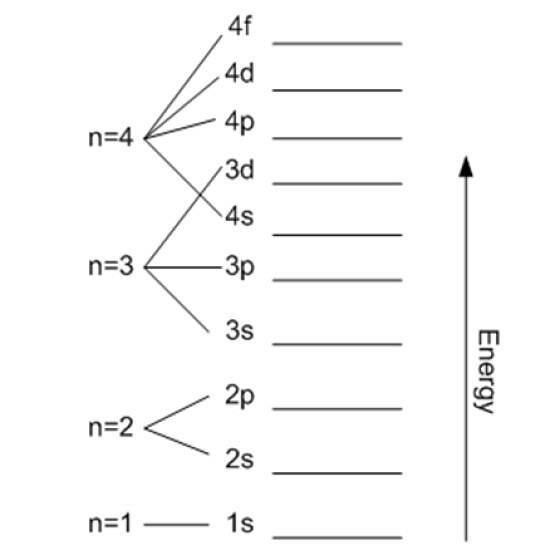
Com exceção da primeira camada, as outras são subdivididas em subcamadas ou subníveis. Cada camada tem uma energia em elétron volt dada por:

- K (n = 1)
- L (n = 2)
- M (n = 3)
- N (n = 4)
- O (n = 5)
- P (n = 6)
- Q (n = 7).
Em teoria não há limite superior para n, mas na prática observa-se que ele atinge apenas n = 8. A menor energia possível corresponde a n = 1 e é a do estado fundamental.
Número quântico do momento azimutal ou angular
Denotado pela letra itálica, este número determina a forma dos orbitais, quantificando a magnitude do momento angular orbital do elétron.
Pode assumir valores positivos e inteiros entre 0 e n-1, por exemplo:
-Quando n = 1, então ℓ = 0 e há apenas um subnível.
-Se n = 2, então ℓ pode ser igual a 0 ou 1, então temos dois subníveis.
-E se n = 3, então ℓ assume os valores 0, 1 e 2 e há 3 subníveis.
Pode ser continuado desta forma indefinidamente, embora como dito antes, na prática n sobe para 8. Os subníveis são denotados pelas letras: s, p, d, F Y g e eles estão aumentando em energia.

Número quântico magnético mℓ
Este número decide a orientação do orbital no espaço e seu valor depende daquele de ℓ.
Para um dado ℓ, existem (2ℓ + 1) valores inteiros de m ℓ, que correspondem aos respectivos orbitais. Estes são:
-ℓ, (- ℓ + 1),… 0,… (+ ℓ -1), + ℓ.
Exemplo
Se n = 2, sabemos que ℓ = 0 e ℓ = 1, então m ℓ assume os seguintes valores:
-Para ℓ = 0: m ℓ = 0.
-Para ℓ = 1: m ℓ = -1, m ℓ = 0, m ℓ = +1
O orbital n = 2 tem dois subníveis, o primeiro com n = 2, ℓ = 0 e m ℓ = 0. Então temos o segundo subnível: n = 2, ℓ = 1, com 3 orbitais:
- n = 2, ℓ = 1, m ℓ = -1
- n = 2, ℓ = 1, m ℓ = 0
- n = 2, ℓ = 1, m ℓ = +1
Os três orbitais têm a mesma energia, mas orientação espacial diferente.
Número quântico de spin ms
Ao resolver a equação de Schrödinger em três dimensões, surgem os números já descritos. No entanto, no hidrogênio uma estrutura ainda mais fina é observada que esses números não são suficientes para explicar.
Por essa razão, em 1921 outro físico, Wolfgang Pauli, propôs a existência de um quarto número: o número de spin ms, que assume valores de + ½ ou -½.
Este número descreve uma propriedade muito importante do elétron, que é o rodar, palavra que vem do inglês rodar (para ligar a si mesmo). E o spin, por sua vez, está relacionado às propriedades magnéticas do átomo.
Uma maneira de entender o spin é imaginar que o elétron se comporta como um minúsculo dipolo magnético (um ímã com pólos norte e sul), graças a uma rotação em torno de seu próprio eixo. A rotação pode ser na mesma direção do sentido horário ou na direção oposta.
Embora Pauli sugerisse a existência desse número, os resultados de um experimento realizado por Otto Stern e Walter Gerlach em 1922 já o previam..
Esses cientistas conseguiram dividir um feixe de átomos de prata em dois, aplicando um campo magnético não uniforme.
O valor de ms não depende de n, ℓ e m ℓ. Na forma gráfica, é representado por uma seta: uma seta para cima indica uma rotação no sentido horário e uma seta para baixo indica uma rotação no sentido anti-horário.
Princípio de Exclusão de Pauli
O comportamento dos elétrons no átomo é resumido no princípio de exclusão de Pauli, que afirma que dois elétrons em um átomo não podem existir no mesmo estado quântico..
Portanto, cada elétron deve ter um conjunto diferente de números quânticos n, ℓ, m ℓ e ms.
A importância dos números quânticos e deste princípio reside na compreensão das propriedades dos elementos da tabela periódica: os elétrons são organizados em camadas de acordo com n, e depois em subcamadas de acordo com ℓ e o resto dos números.
Referências
- Alonso, M. 1971. Quantum and statistics foundations. Fundo Educacional Interamericano.
- Bauer, W. 2011. Physics for Engineering and Sciences. Volume 1. Mc Graw Hill.
- Chang, R. 2013. Chemistry. 11º. Edição. Educação Mc Graw Hill.
- Eisberg-Resnick. 1989. Quantum Physics. Limusa - Wiley.
- Giambattista, A. 2010. Física. 2ª Ed. McGraw Hill.
- Rex, A. 2011. Fundamentals of Physics. Pearson.
- Tippens, P. 2011. Physics: Concepts and Applications. 7ª Edição. Colina Mcgraw.


Ainda sem comentários