
Números ímpares como distingui-los, exemplos e exercícios
O números ímpares são aqueles números inteiros que não são divisíveis por 2. Isso significa que com quantidades ímpares você não pode fazer grupos de 2, por exemplo, se alguém tiver 9 doces para compartilhar com um amigo e não quiser dividir nenhum, um terá 4 doces e os outros 5.
Alguns dos números ímpares são os seguintes: ... -5, -3, -1, 1, 3, 5, 7, 9, 11, 13 ... Nesta expressão, as reticências indicam que há mais números, tanto à esquerda quanto à direita.

Olhando de perto, você pode ver que cada número ímpar pode ser obtido adicionando 2 ao número anterior. Por exemplo, se adicionarmos 2 a -1 obtemos 1, se fizermos 1 + 2 obteremos 3 e assim por diante.
Observa-se também que se os pares forem intercalados, incluindo 0, que é considerado um número par, obtém-se o conjunto de inteiros Z.
É por isso que qualquer número natural ímpar pode ser escrito na forma 2n + 1, onde n = 0, ± 1, ± 2, ± 3, ± 4, ± 5 ..., onde o símbolo ± significa que n pode ser considerado positivo ou como negativo.
No caso de números maiores, pode ser reconhecido quando é ímpar, pois sempre termina em 1, 3, 5, 7 ou 9. Por exemplo, 1571 é ímpar e, portanto, é o número inteiro negativo -152,489.
Índice do artigo
- 1 Números ímpares na natureza e na cultura popular
- 1.1 Números primos
- 2 operações de número ímpar
- 2.1 - Somas e produtos
- 2.2 - Poderes
- 3 exercícios resolvidos
- 3.1 - Exercício 1
- 3.2 - Exercício 2
- 3.3 - Exercício 3
- 4 referências
Números ímpares na natureza e na cultura popular
Os números ímpares ocorrem com freqüência na natureza, e entre eles o número 3 é de significado especial. Vejamos alguns exemplos:
-Existem muitas flores com um número ímpar de pétalas.
-Temos 5 dedos em cada mão.
-Os humanos têm 23 pares de cromossomos.
-Existem as 3 leis de Newton e as 3 leis da termodinâmica.
-Os núcleos de átomos que possuem um número ímpar de prótons e nêutrons são menos estáveis do que aqueles com um número par.
-Os sábios são 3.
-Em contos e contos, o número 3 aparece com frequência, por exemplo, romances como Os três Mosqueteiros por Alexandre Dumas e em contos populares como Os três irmãos Y Os três Porquinhos.
-Para a composição artística existe a chamada regra estranha, que estabelece que uma composição com um número ímpar de elementos é mais atraente do que uma com um número par. O número ímpar adiciona dinamismo, enquanto um número par adiciona estabilidade.

-Uma estratégia comum para fazer os preços dos itens parecerem mais baratos é fazer com que terminem em 9, digamos $ 2,99, $ 39 e assim por diante..
-O número 13 é considerado azarado por alguns, enquanto outros atribuem qualidades místicas ao 11, ambos números ímpares..
números primos
Os números primos, aqueles que apenas se admitem e 1 como divisores, são ímpares, com exceção de 2, que é o único número primo par.
É possível mostrar que qualquer número pode ser decomposto como produto de fatores primos (incluindo potências destes), e que esta forma de expressar o número é única, exceto na ordem dos fatores..
Por exemplo, o número 45 pode ser decomposto como 45 = 33 x 5.
Operações com números ímpares
Com números ímpares, todas as operações aritméticas são realizadas, e algumas têm características salientes.
- Somas e produtos
-A soma de dois números ímpares resulta em um número par: 3 + 5 = 8; 11 + 15 = 26; (-10) + (+6) = - 4.
-Ao adicionar um número ímpar a um número par, o resultado é ímpar: 7 + 2 = 9; 26+ 9 = 35; (-5) + 12 = 7.
-Se o n primeiros números naturais, ímpares e consecutivos, o resultado é ndois. Vejamos isso com um pouco mais de detalhes:
Para n = 2: 1 + 3 = 4 = 2dois
Para n = 3: 1 + 3 + 5 = 9 = 3dois
Para n = 4: 1 + 3 + 5 + 7 = 16 = 4dois
-Quando um ímpar é multiplicado por um par, um número par é produzido: 7 x 4 = 28; (-3) x 12 = -36.
-Multiplicar dois números ímpares também resulta em um ímpar: 3 x 5 = 15; (-5) x (+11) = -55.
- Poderes
-Quando um número positivo é elevado a uma potência ímpar, resulta um número positivo, por exemplo: 33 = 27.
-Ao elevar um número negativo a uma potência ímpar, o resultado é negativo: (-2)3= (-2) x (-2) x (-2) = -8.
-As potências ímpares de inteiros positivos podem ser alcançadas se os números ímpares forem organizados como mostrado na figura e as linhas forem adicionadas:
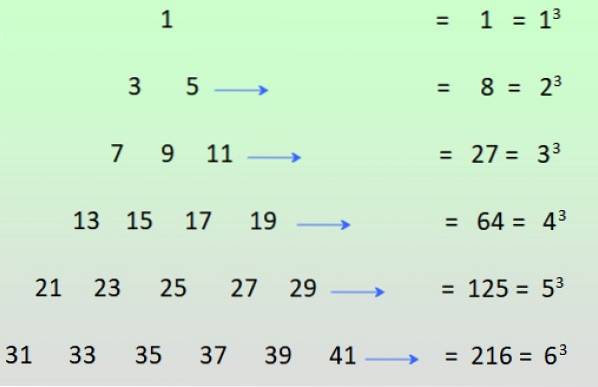
Exercícios resolvidos
- Exercício 1
Decida se o resultado da seguinte operação é ímpar ou par:
(53476890083 + 1987628967) x 13567903
Solução
Para obter a resposta, você não precisa correr para encontrar uma calculadora, mas sim aplicar as propriedades vistas. Vejamos os últimos dígitos dos adendos, que são 3 e 7, respectivamente:
53476890083 + 1987628967
Isso significa que os adendos são ímpares e já sabemos que a soma de dois números ímpares é par.
Portanto, o número que resulta dos parênteses é par e vamos multiplicá-lo por um número que termina em 3:
13567903
O que significa que este número é ímpar.
Nas propriedades descritas acima foi estabelecido que a multiplicação de pares por ímpares resulta em um número par. Portanto, a operação resultante é uniforme.
- Exercício 2
Quanto vale a soma dos primeiros 5 números ímpares consecutivos? E os primeiros 50?
Solução
A soma dos primeiros 5 números ímpares consecutivos é:
1 + 3 + 5 + 7 + 9 = 25
Mas se quisermos adicionar os primeiros 50 dessa forma, será complicado, então vamos para as propriedades. Eles afirmam que a soma dos números ímpares consecutivos é ndois. Neste caso, n = 50 e a soma solicitada é:
cinquentadois = 50 x 50 = 2500.
- Exercício 3
Quando você soma três números ímpares consecutivos, obtém 237. Quais são os números?
Solução
Chamemos nosso primeiro número ímpar de x, e o segundo ez de terceiro, de acordo com a afirmação de que é verdade que:
x + y + z = 237
Na linguagem algébrica, qualquer número ímpar pode ser escrito na forma 2n +1. Vamos fazer com que nosso primeiro número ímpar seja:
x = 2n +1
Vamos adicionar 2 para obter o próximo ímpar:
y = x + 2 = (2n + 1) + 2 = 2n + 3
E, finalmente, 2 é adicionado novamente para obter a terceira ímpar:
z = (2n +3) + 2 = 2n + 5
Tudo isso se soma:
2n + 1 + 2n + 3 + 2n + 5 = 237
6n + 9 = 237
O que resulta em uma equação linear simples, cuja solução é:
n = 38
E agora com o valor de n = 38 existem os três números solicitados:
x = (2 × 38) + 1 = 77
Os seguintes são ímpares consecutivos, portanto:
y = 79
z = 81
E o leitor pode verificar facilmente que a soma dos três é 237.
Referências
- Baldor, A. 1986. Arithmetic. Edições e distribuições do Codex.
- Barrios, L. Números ímpares e potências dos números naturais. Recuperado de: sinewton.org.
- Brilhante. Números pares e ímpares. Recuperado de: brilhante.org.
- Matemática 18. Operações com números ímpares. Recuperado de: matematicas18.com.
- Wikipedia. Números pares e ímpares. Recuperado de: es.wikipedia.org.


Ainda sem comentários