O números irracionais são aqueles cuja expressão decimal tem números infinitos sem um padrão de repetição, portanto, eles não podem ser obtidos fazendo o quociente entre quaisquer dois inteiros.
Entre os números irracionais mais conhecidos estão:
Entre eles, sem dúvida π (pi) é o mais familiar, mas existem muitos mais. Todos eles pertencem ao conjunto dos números reais, que é o conjunto numérico que agrupa os números racionais e irracionais..
As reticências na figura 1 indicam que os decimais continuam indefinidamente, o que ocorre é que o espaço das calculadoras comuns só permite mostrar alguns.
Se observarmos com atenção, sempre que fizermos o quociente entre dois números inteiros, obteremos um decimal com algarismos limitados ou, se não, com algarismos infinitos em que um ou mais se repetem. Bem, isso não acontece com números irracionais..
Índice do artigo
O grande matemático Pitágoras, nascido em 582 aC em Samos, Grécia, fundou a escola de pensamento pitagórica e descobriu o famoso teorema que leva seu nome. Temos aqui embaixo à esquerda (talvez os babilônios já soubessem disso há muito tempo).
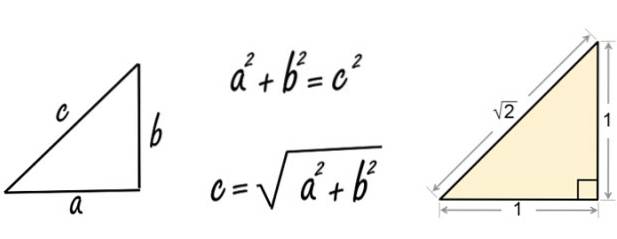
Bem, quando Pitágoras (ou provavelmente um discípulo dele) aplicou o teorema a um triângulo retângulo com lados iguais a 1, ele encontrou o número irracional √2.
Ele fez assim:
c = √1dois + 1dois = √1 + 1 = √2
E imediatamente percebeu que esse novo número não vinha do quociente entre dois outros números naturais, que eram os conhecidos naquela época.
Portanto, ele chamou irracional, e a descoberta causou grande ansiedade e confusão entre os pitagóricos.
-O conjunto de todos os números irracionais é denotado pela letra I e às vezes como Q * ou QC. A união entre os números irracionais I ou Q * e os números racionais Q, dá origem ao conjunto de números reais R.
-Com números irracionais, as operações aritméticas conhecidas podem ser realizadas: adição, subtração, multiplicação, divisão, capacitação e muito mais.
-A divisão por 0 também não é definida entre números irracionais.
-A soma e o produto entre os números irracionais não é necessariamente outro número irracional. Por exemplo:
√2 x √8 = √16 = 4
E 4 não é um número irracional.
-No entanto, a soma de um número racional mais um número irracional resulta em um irracional. Desta maneira:
1 + √2 = 2,41421356237…
-O produto de um número racional diferente de 0 por um número irracional também é irracional. Vejamos este exemplo:
2 x √2 = 2,828427125…
-O inverso de um irracional resulta em outro número irracional. Vamos tentar alguns:
1 / √2 = 0,707106781…
1 / √3 = 0,577350269…
Esses números são interessantes porque também são os valores de algumas razões trigonométricas de ângulos conhecidos. A maioria das razões trigonométricas são números irracionais, mas há exceções, como sin 30º = 0,5 = ½, o que é racional.
-Além disso, as propriedades comutativas e associativas são satisfeitas. Se aeb são dois números irracionais, isso significa que:
a + b = b + a.
E se c for outro número irracional, então:
(a + b) + c = a + (b + c).
-A propriedade distributiva da multiplicação com respeito à adição é outra propriedade bem conhecida que também se aplica aos números irracionais. Neste caso:
a. (b + c) = a.b + a.c.
-Um a irracional tem seu oposto: -a. Quando eles são somados, o resultado é 0:
a + (- a) = 0
-Entre dois racionais diferentes, há pelo menos um número irracional.
A linha real é uma linha horizontal onde os números reais estão localizados, dos quais os irracionais são uma parte importante.
Para encontrar um número irracional na linha real, na forma geométrica, podemos usar o teorema de Pitágoras, uma régua e um compasso.
Como exemplo, vamos localizar √5 na linha real, para a qual desenhamos um triângulo retângulo com lados x = 2 Y y = 1, como mostra a imagem:
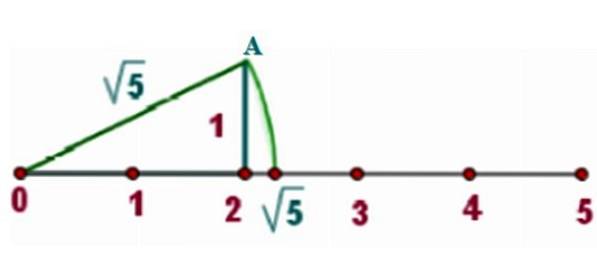
Pelo teorema de Pitágoras, a hipotenusa de tal triângulo é:
c = √2dois + 1dois = √4 + 1 = √5
Agora a bússola é colocada com o ponto em 0, onde também está um dos vértices do triângulo retângulo. A ponta do lápis da bússola deve estar no vértice A.
Um arco de circunferência é desenhado que corta a linha real. Uma vez que a distância entre o centro da circunferência e qualquer ponto sobre ela é o raio, que é igual a √5, o ponto de interseção também está longe de √5 do centro.
No gráfico, pode-se ver que √5 está entre 2 e 2,5. Uma calculadora nos dá o valor aproximado de:
√5 = 2,236068
E assim, ao construir um triângulo com os lados apropriados, outros irracionais podem ser localizados, como √7 e outros.
Os números irracionais são classificados em dois grupos:
-Algébrico
-Transcendente ou transcendental
Os números algébricos, que podem ou não ser irracionais, são soluções de equações polinomiais cuja forma geral é:
paran xn + paran-1xn-1 + paran-2xn-2 +… + a1x + aou = 0
Um exemplo de uma equação polinomial é uma equação quadrática como esta:
x3 - 2x = 0
É fácil mostrar que o número irracional √2 é uma das soluções desta equação.
Por outro lado, os números transcendentes, embora sejam irracionais, nunca surgem como solução de uma equação polinomial..
Os números transcendentes mais encontrados na matemática aplicada são π, devido à sua relação com a circunferência e o número e, ou número de Euler, que é a base dos logaritmos naturais..
Um quadrado cinza é colocado em um quadrado preto na posição indicada na figura. A superfície do quadrado preto é conhecida por ter 64 cmdois. Qual é o comprimento de ambos os quadrados?
A área de um quadrado com o lado L é:
A = Ldois
Uma vez que o quadrado preto tem 64 cmdois de área, seu lado deve ser de 8 cm.
Esta medição é a mesma que a diagonal do quadrado cinza. Aplicando o teorema de Pitágoras a esta diagonal, e lembrando que os lados de um quadrado medem o mesmo, teremos:
8dois = Lgdois + eugdois
Onde Lg é o lado do quadrado cinza.
Portanto: 2Lgdois = 8dois
Aplicando raiz quadrada a ambos os lados da igualdade:
eug = (8 / √2) cm
Ainda sem comentários