
Números pares como identificá-los, exemplos, exercícios

O números pares são todos aqueles que podem ser divididos exatamente por 2, por exemplo 0, 2, 4, 6, 8, 10, 12, 14, 16, 18 ... Entre os números negativos também há pares: -2, -4, - 6, - 8, -10 ...
Se olharmos com atenção para os números que seguem 8 na sequência de números positivos: 10, 12, 14, 16 e 18, pode-se ver que eles terminam em 0, 2, 4, 6 e 8 respectivamente. Com isso em mente, os seguintes números pares podem ser construídos: 20, 22, 24, 26, 28, 30, 32, 34, 36, 38 ...
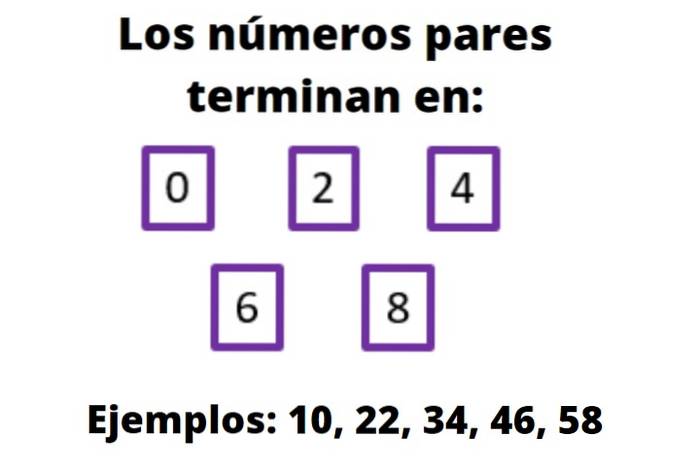
Conclui-se que para identificar qualquer par, por maior que seja, ou se tiver sinal negativo, observe o dígito onde termina. Se for 0, 2, 4, 6 ou 8, estamos na presença de um número par. Por exemplo: 1554, 3578, -105.962 e assim por diante.
Uma vez que todo número par é divisível por exatamente 2, podemos obter um número par de qualquer outro simplesmente multiplicando por 2. Segue-se que a forma geral de qualquer número par é:
2n
Onde n é um número inteiro: ... -2, -1, 1, 2, 3, 4, 5, ...
E o que acontece com os números que estão entre os pares, como 3, 5, 7 e mais?
Bem, eles são os números ímpares. Dessa forma, os números inteiros podem ser classificados nessas duas categorias amplas: ímpares e pares. Esta qualidade dos números é chamada paridade.
Y como vemos de las secuencias numéricas, los pares y los impares están intercalados, es decir, si comenzamos por el 0, que es par, sigue el 1, que es impar, luego el 2 que es par, después el 3 que es impar e assim por diante.
Índice do artigo
- 1 Exemplos de números pares
- 2 Operações e propriedades de números pares
- 3 exercícios resolvidos
- 3.1 - Exercício 1
- 3.2 - Exercício 2
- 3.3 - Exercício 3
- 4 referências
Exemplos de números pares
Enquanto houver quantidades inteiras, algumas delas podem ser uniformes e estão presentes na natureza e em muitas situações da vida real. Se temos uma certa quantidade com a qual grupos de dois podem ser formados, essa quantidade é par. Por exemplo:
-No total, os dedos das mãos são 10, que é um número par. Também temos número par de olhos, braços, orelhas, pernas e pés.
-Os insetos quase sempre possuem 2 pares de asas, ou seja, possuem 4 asas no total, também possuem 3 pares de patas, num total de 6 patas e 2 antenas.
-Temos 2 pais, 4 avós, 8 bisavós, 16 tataravós e assim por diante na árvore genealógica. Estes são todos números pares.
-Existem flores com número par de pétalas, incluindo algumas margaridas que têm até 34.

-O júri é geralmente composto por 12 pessoas.
-Esportes como tênis, boxe, esgrima, luta livre e xadrez são praticados entre 2 pessoas. No tênis há partidas entre casais.
-Uma equipe de vôlei é composta por 6 jogadores na quadra.
-O tabuleiro de xadrez tem 64 casas e 2 conjuntos de peças: brancas e pretas. O conjunto possui 16 peças com os seguintes nomes: rei, rainha, bispo, cavalo e peão, todos com número par de peças, exceto o rei e a rainha que são únicos. Desta forma, cada jogador tem 2 bispos, 2 torres, 2 cavalos e 8 peões..
Operações e propriedades de números pares
Com os números pares, você pode realizar todas as operações aritméticas conhecidas: somar, subtrair, multiplicar, dividir, aumentar e muito mais. Em resumo, todas as operações permitidas podem ser feitas com os inteiros, dos quais os números pares fazem parte.
No entanto, os resultados dessas operações apresentam algumas peculiaridades. As coisas notáveis que podemos observar nos resultados são as seguintes:
-Os números pares são apresentados intercalados entre os ímpares, como vimos anteriormente.
-Sempre que adicionamos dois ou mais números pares, o resultado é par. Vamos ver:
2 + 18 + 44 + 4 = 68
-Mas se somarmos dois números, um par e um ímpar, o resultado é ímpar. Por exemplo, 2 + 3 = 5 ou 15 + 24 = 39.
-Multiplicando dois números pares, também obteremos um número par. O mesmo acontece se multiplicarmos um ímpar ou par. Para ver isso, vamos fazer algumas operações simples, como:
Par x par: 28 x 52 = 1456
Ímpar x par: 12 x 33 = 396
Em vez disso, o produto de dois números ímpares é sempre ímpar.
-Qualquer número elevado a uma potência par é positivo, independentemente do sinal do número:
dois4 = 2 x 2 x 2 x 2 = 16
(-5)dois = (-5) x (-5) = 25
(-3)4 = (-3) x (-3) x (-3) x (-3) = 81
-sim para é um número tal que paradois é mesmo assim para é mesmo. Vamos examinar os primeiros quadrados para ver se eles se originam de números pares:
4, 9,16, 25, 36, 49, 64, 81, 100, 121, 144, 169, 196, 225 ...
Na verdade, é verdade que: 2dois = 4 e 2 é par; 16 = 4dois, 36 = 6dois e assim.
Em vez disso, 25 é o quadrado de 5, que é ímpar, 49 é o quadrado de 7, que também é ímpar.
-O resto entre a divisão de um par e outro par também é par. Por exemplo, se dividirmos 100 por 18, o quociente é 5 e o restante é 10.
Exercícios resolvidos
- Exercício 1
Identifique quais são números pares e quais são ímpares:
12, 33, 46, 51, 69, 70, 82, 98, 100, 101, 121, 134, 145, 159, 162, 177, 183, 196.
Solução
12, 46, 70, 82, 98, 100, 134, 162, 196.
- Exercício 2
Três números pares consecutivos somam 324. Quais são os números?
Solução
Sejamos qualquer número que chamaremos de “n”. Como não sabemos se é par ou não, certificamo-nos de que está com o critério dado no início, aquele que diz que um número par é da forma 2n.
O número consecutivo a 2n é 2n + 1, mas isso é estranho, porque sabemos que eles são intercalados, então adicionamos de volta 1: 2n +2.
E com isso o terceiro número é: 2n + 4.
Agora que temos os três números pares consecutivos prontos, nós os somamos e igualamos a soma a 324, conforme a declaração requer:
2n + 2n + 2 + 2n + 4 = 324
Adicionamos todos os termos “2n”, uma vez que são semelhantes, e também os números à esquerda da igualdade:
6n + 6 = 324 → 6n = 318
n = 53
Mas atenção, n = 53 não é um número par e não faz parte dos números que o problema nos pede. O comunicado diz que são "três números pares consecutivos".
Na verdade, o primeiro número que procuramos é: 2n = 2 x 53 = 106.
O próximo é 108 e o terceiro é 110.
Se somarmos os três números, vemos que 324 é realmente obtido:
106 + 108 + 110 = 324
- Exercício 3
Encontre uma fórmula para obter o vigésimo número natural par, começando de 0 e encontre este número, verificando manualmente.
Solução
Lembrando que 0 é o primeiro número par, depois vem o 2, depois o 4 e assim intercalado, pensemos em uma fórmula que nos permite obter 0 a partir de outro número, também natural.
Esta fórmula pode ser:
2n - 2, com n = 1, 2, 3, 4, 5 ... .
Com ele obtemos 0 fazendo n = 1:
2,1 - 2 = 0
Agora vamos fazer n = 2 e obter o par 2
2,2 - 2 = 2
Tomando n = 3 resultados no par 4:
2,3 - 2 = 4
Finalmente fazendo n = 20:
- 20 - 2 = 40 - 2 = 38
O vigésimo par é 38 e nós o verificamos:
0, 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28, 30, 32, 34, 36, 38
O leitor pode dizer qual será o centésimo e quinto número par usando a fórmula?
Referências
- Baldor, A. 1986. Arithmetic. Edições e distribuições do Codex.
- A matemática é divertida. Números pares e ímpares. Recuperado de mathisfun.com.
- Oficina de Matemática. Dualidade par-ímpar. Recuperado de: ehu.eus.
- Wikipedia. Paridade de zero. Recuperado de: es.wikipedia.org.
- Wikipedia. Paridade. Recuperado de: en.wikipedia.org.



Ainda sem comentários