
Propriedades, exemplos e operações de números racionais
O números racionais são todos os números que podem ser obtidos como a divisão de dois números inteiros. Exemplos de números racionais são: 3/4, 8/5, -16/3 e aqueles que aparecem na figura a seguir. Em um número racional é indicado o quociente, sendo possível fazê-lo posteriormente se necessário.
A figura representa qualquer objeto, redondo por conveniência. Se quisermos dividi-lo em 2 partes iguais, como à direita, temos duas metades restantes e cada uma vale 1/2.
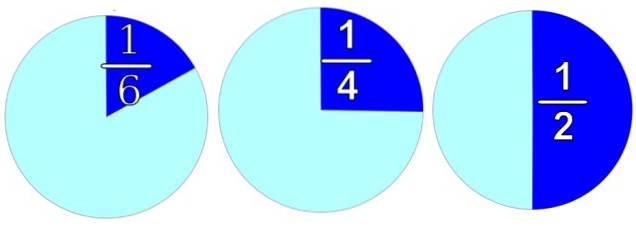
Dividindo em 4 partes iguais, teremos 4 peças e cada uma vale 1/4, como na imagem ao centro. E se for necessário distribuí-lo em 6 partes iguais, pois cada parte valeria 1/6, o que vemos na imagem à esquerda.
Claro, também poderíamos dividi-lo em duas partes desiguais, por exemplo, poderíamos manter 3/4 partes e salvar 1/4 parte. Outras divisões também são possíveis, como 4/6 partes e 2/6 partes. O importante é que a soma de todas as partes seja 1.
Desta forma, é evidente que com números racionais, coisas como comida, dinheiro, terra e todos os tipos de objetos podem ser divididos, contados e distribuídos em frações. E assim a quantidade de operações que podem ser feitas com os números é expandida.
Os números racionais também podem ser expressos na forma decimal, como pode ser visto nos seguintes exemplos:
1/2 = 0,5
1/3 = 0,3333…
3/4 = 0,75
1/7 = 0,142857142857142857…
Mais tarde iremos indicar como ir de um formulário para outro com exemplos.
Índice do artigo
- 1 Propriedades dos números racionais
- 2 exemplos de números racionais
- 2.1 Representação decimal de um número racional
- 3 operações com números racionais
- 3.1 - Adição e subtração
- 3.2 - Multiplicação e divisão
- 4 referências
Propriedades dos números racionais
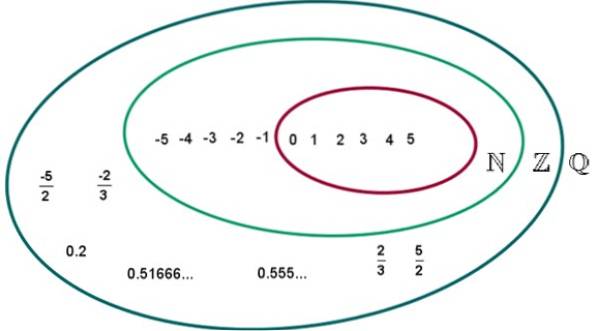
Os números racionais, cujo conjunto denotaremos com a letra Q, têm as seguintes propriedades:
-Q inclui os números naturais N e os números inteiros Z.
Levando em consideração que qualquer número para Pode ser expresso como o quociente entre ele mesmo e 1, é fácil ver que entre os números racionais também existem números naturais e inteiros.
Assim, o número natural 3 pode ser escrito como uma fração e também -5:
3 = 3/1
-5 = -5/1 = 5 / -1 = - (5/1)
Desse modo, Q é um conjunto numérico que inclui um maior número de números, algo muito necessário, já que os números "redondos" não são suficientes para descrever todas as operações possíveis a serem feitas..
-Os números racionais podem ser somados, subtraídos, multiplicados e divididos, sendo o resultado da operação um número racional: 1/2 + 1/5 = 7/10; 1/2 - 1/5 = 3/10; (1/2) x (1/5) = 1/10; (1/2) ÷ (1/5) = 5/2.
-Entre cada par de números racionais, outro número racional sempre pode ser encontrado. Na verdade, entre dois números racionais, existem números racionais infinitos.
Por exemplo, entre os racionais 1/4 e 1/2 estão os racionais 3/10, 7/20, 2/5 (e muitos mais), que podem ser verificados expressando-os como decimais.
-Qualquer número racional pode ser expresso como: i) um número inteiro ou ii) um número decimal limitado (estrito) ou periódico: 4/2 = 2; 1/4 = 0,25; 1/6 = 0,166666666…
-O mesmo número pode ser representado por infinitas frações equivalentes e todas elas pertencem a Q. Vejamos este grupo:

Todos eles representam o decimal 0,428571 ...
-De todas as frações equivalentes que representam o mesmo número, a fração irredutível, a mais simples de todas, é a representante canônico desse número. O representante canônico do exemplo acima é 3/7.
Exemplos de números racionais
-Frações próprias, aquelas em que o numerador é menor que o denominador:

-Frações impróprias, cujo numerador é maior que o denominador:

-Números naturais e números inteiros:

-Frações equivalentes:


Representação decimal de um número racional
Quando o numerador é dividido pelo denominador, a forma decimal do número racional é encontrada. Por exemplo:
2/5 = 0,4
3/8 = 0,375
1/9 = 0,111111…
6/11 = 0,545454…
Nos primeiros dois exemplos, o número de casas decimais é limitado. Isso significa que quando a divisão é feita, finalmente obtemos um resto de 0.
Por outro lado, nos próximos dois, o número de casas decimais é infinito e por isso as reticências são colocadas. No último caso, há um padrão nas casas decimais. No caso da fração 1/9, o número 1 se repete indefinidamente, enquanto em 11/06 é 54.
Quando isso acontece, o decimal é considerado periódico e é denotado por um acento circunflexo como este:


Transforme um decimal em uma fração
Se for um decimal limitado, a vírgula é simplesmente eliminada e o denominador se torna a unidade seguida por tantos zeros quantos forem os números no decimal. Por exemplo, para transformar o decimal 1,26 em uma fração, escreva assim:
1,26 = 126/100
Em seguida, a fração resultante é simplificada ao máximo:
126/100 = 63/50
Se o decimal for ilimitado, o período será identificado primeiro. Em seguida, essas etapas são seguidas para encontrar a fração resultante:
-O numerador é a subtração entre o número (sem vírgula ou circunflexo) e a parte que não leva o acento circunflexo.
-O denominador é um número inteiro com tantos 9 quanto houver números sob o circunflexo, e tantos 0 quanto houver números em a parte decimal existem que não estão sob o circunflexo.
Vamos seguir este procedimento para transformar o número decimal 0,428428428 ... em uma fração.
-Primeiro, o período é identificado, que é a sequência que se repete: 428.

-Em seguida, a operação de subtrair o número sem vírgula ou acento é feita: 0428 da parte que não tem circunflexo, que é 0. Portanto, é 428 - 0 = 428.
-O denominador é construído, sabendo-se que sob o circunflexo existem 3 algarismos e todos estão sob o circunflexo. Portanto, o denominador é 999.
-Finalmente, a fração é formada e simplificada se possível:
0,428 = 428/999
Não é possível simplificar mais.
Operações com números racionais
- Adição e subtração
Frações com o mesmo denominador
Quando as frações têm o mesmo denominador, somar e / ou subtrair é muito fácil, pois os numeradores são simplesmente somados algebricamente, deixando os mesmos adendos como denominador do resultado. Finalmente, se possível, é simplificado.
Exemplo
Faça a seguinte adição algébrica e simplifique o resultado:

A fração resultante já é irredutível.
Frações com denominadores diferentes
Neste caso, os adendos são substituídos por frações equivalentes com o mesmo denominador e então segue-se o procedimento já descrito.
Exemplo
Adicione algebricamente os seguintes números racionais, simplificando o resultado:

As etapas são:
-Determine o mínimo múltiplo comum (LCM) dos denominadores 5, 8 e 3:
lcm (5,8,3) = 120
Este será o denominador da fração resultante sem simplificar.
-Para cada fração: divida o MMC pelo denominador e multiplique pelo numerador. O resultado desta operação é colocado, com seu respectivo sinal, no numerador da fração. Dessa forma, obtém-se uma fração equivalente ao original, mas com o LCM como denominador..
Por exemplo, para a primeira fração, o numerador é construído assim: (120/5) x 4 = 96 e obtemos:

Proceda da mesma forma para as demais frações:



Finalmente, as frações equivalentes são substituídas sem esquecer seu sinal e a soma algébrica dos numeradores é realizada:
(4/5) + (14/8) - (11/3) + 2 = (96/120) + (210/120) - (440/120) + (240/120) =
= (96 + 210-440 + 24) / 120 = -110 / 120 = -11/12
- Multiplicação e divisão
A multiplicação e divisão são feitas seguindo as regras mostradas abaixo:
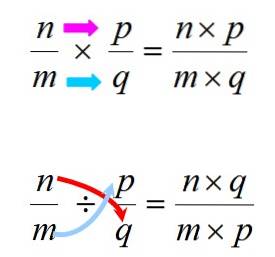
Em qualquer caso, é importante lembrar que a multiplicação é comutativa, o que significa que a ordem dos fatores não altera o produto. Isso não acontece com a divisão, portanto, deve-se ter cuidado para respeitar a ordem entre dividendo e divisor.
Exemplo 1
Realize as seguintes operações e simplifique o resultado:
a) (5/3) x (8/15)
b) (-4/5) ÷ (2/9)
Responda para
(5/3) x (8/15) = (5 x 8) / (3 x 15) = 15/120 = 1/8
Resposta b
(-4/5) ÷ (2/9) = (-4 x 9) / (5 x 2) = -36 / 10 = -18/5
Exemplo 2
Luisa tinha $ 45. Ele gastou um décimo comprando um livro e 2/5 do que sobrou em uma camiseta. Quanto dinheiro sobrou para Luisa? Expresse o resultado como uma fração irredutível.
Solução
O livro custa (1/10) x $ 45 = 0,1 x $ 45 = $ 4,5
Portanto, Luisa ficou com:
45 - 4,5 $ = 40,5 $
Com esse dinheiro Luisa foi até a loja de roupas e comprou a camisa, cujo preço é:
(2/5) x $ 40,5 = $ 16,2
Agora Luisa tem em seu portfólio:
40,5 - 16,2 $ = 24,3 $
Para expressá-lo como uma fração, é escrito assim:
24,3 = 243/10
Isso é irredutível.
Referências
- Baldor, A. 1986. Arithmetic. Edições e distribuições do Codex.
- Carena, M. 2019. Manual of Mathematics. Universidade Nacional do Litoral.
- Figuera, J. 2000. Mathematics 8. Ediciones Co-Bo.
- Jiménez, R. 2008. Algebra. Prentice Hall.
- Os números racionais. Recuperado de: Cimanet.uoc.edu.
- Números racionais. Recuperado de: webdelprofesor.ula.ve.


Ainda sem comentários