
Números transcendentes o que são, fórmulas, exemplos, exercícios
O números transcendentes são aqueles que não podem ser obtidos como resultado de uma equação polinomial. O oposto de um número transcendente é um número algébrico, que são soluções de uma equação polinomial do tipo:
paran xn + paran-1 xn-1 +… + Adois xdois + para1 x + a0 = 0
Onde os coeficientes an, paran-1,… paradois, para1, para0 são números racionais, chamados de coeficientes do polinômio. Se um número x é uma solução para a equação anterior, então esse número não é transcendente.

Vamos analisar alguns números e ver se são transcendentes ou não:
a) 3 não é transcendente porque é uma solução de x - 3 = 0.
b) -2 não pode ser transcendente porque é uma solução de x + 2 = 0.
c) ⅓ é uma solução de 3x - 1 = 0
d) Uma solução da equação xdois - 2x + 1 = 0 é √2 -1, então esse número por definição não é transcendente.
e) Nem √2 porque é o resultado da equação xdois - 2 = 0. Quadrado √2 dá o resultado 2, que subtraído de 2 é igual a zero. Então, √2 é um número irracional, mas não é transcendente.
Índice do artigo
- 1 O que são números transcendentes?
- 1.1 O número π
- 1.2 O número e
- 2 Fórmulas onde o número transcendente π aparece
- 2.1 O perímetro da circunferência
- 2.2 Área de um círculo
- 2.3 Superfície de uma esfera
- 2.4 Volume da esfera
- 3 exercícios
- 3.1 - Exercício 1
- 3.2 - Exercício 2
- 4 referências
O que são números transcendentes?
O problema é que não existe uma regra geral para obtê-los (mais tarde diremos uma forma), mas alguns dos mais famosos são os números pi e ele Número Neper, denotado respectivamente por: π Y e.
O número π
O número π Parece naturalmente ao observar que o quociente matemático entre o perímetro P de um círculo e seu diâmetro D, independentemente de ser um círculo pequeno ou grande, sempre dá o mesmo número, denominado pi:
π = P / D ≈ 3,14159…
Isso significa que se o diâmetro da circunferência for tomado como unidade de medida, para todos eles, grandes ou pequenos, o perímetro será sempre P = 3,14 ... = π, como pode ser visto na animação da figura 2.
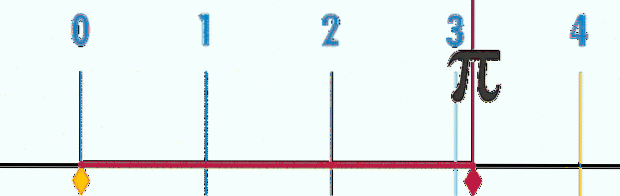
Para determinar mais decimais, é necessário medir P e D com maior precisão e depois calcular o quociente, o que foi feito matematicamente. O ponto principal é que os decimais do quociente não têm fim e nunca se repetem, então o número π além de ser transcendente, também é irracional.
Um número irracional é um número que não pode ser expresso como a divisão de dois números inteiros.
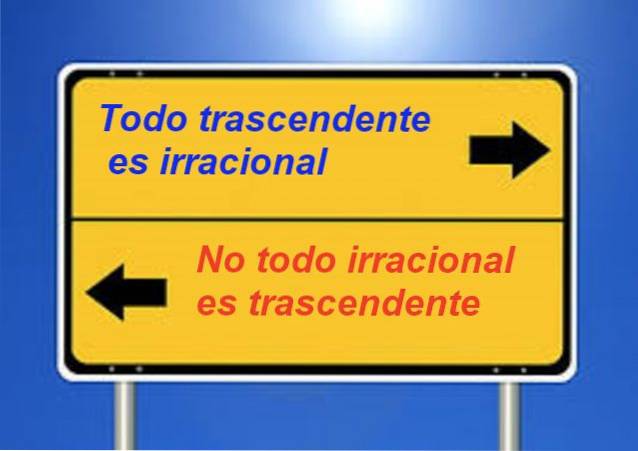
Sabe-se que todo número transcendente é irracional, mas não é verdade que todos os números irracionais são transcendentes. Por exemplo, √2 é irracional, mas não é transcendente.
O número e
O número transcendente e é a base dos logaritmos naturais e sua aproximação decimal é:
e ≈ 2.718281828459045235360… .
Se você quisesse escrever o número e exatamente, seria necessário escrever decimais infinitos, pois todo número transcendente é irracional, como disse antes.
Os primeiros dez dígitos de e são fáceis de lembrar:
2,7 1828 1828 e embora pareça seguir um padrão repetitivo, isso não é alcançado em decimais de ordem superior a nove.
Uma definição mais formal de e É o seguinte:
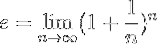
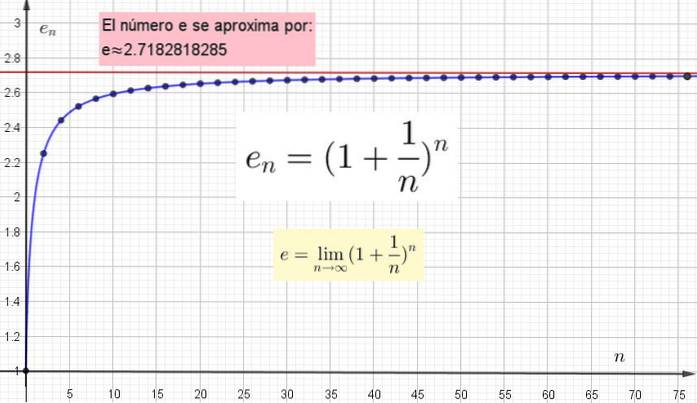
O que significa que o valor exato de e é conseguido realizando a operação indicada nesta fórmula, quando o número natural n tende ao infinito.
Isso explica porque só podemos obter aproximações de e, já que não importa quão grande seja o número n colocado, sempre será possível encontrar um n mais alto.
Vamos procurar algumas aproximações por conta própria:
-Quando n = 100, então (1 + 1/100)100 = 2,70481 que dificilmente coincide na primeira casa decimal com o valor "verdadeiro" de e.
-Se você escolher n = 10.000, você tem (1 + 1 / 10.000)10.000 = 2,71815 que corresponde ao valor "exato" de e nas três primeiras casas decimais.
Este processo teria que ser seguido infinitamente para obter o valor "verdadeiro" de e. Acho que não temos tempo para fazer isso, mas vamos tentar mais um:
Vamos usar n = 100.000:
(1 + 1 / 100.000)100.000 = 2.7182682372
Isso tem apenas quatro casas decimais correspondendo ao valor considerado exato.
O importante é entender que quanto maior o valor de n escolhido para calcular en, quanto mais próximo estiver do valor verdadeiro. Mas esse valor verdadeiro só será obtido quando n for infinito.
Outros números importantes
Além desses números famosos, existem outros números transcendentes, por exemplo:
- dois√2
Cada número algébrico, diferente de 0 ou 1, elevado a um expoente irracional será um número transcendente.
-O número Champernowne na base 10:
C_10 = 0,123456789101112131415161718192021… .
-O número de Champernowne na base 2:
C_2 = 0,1101110010110111… .
-O número gama γ ou constante de Euler-Mascheroni:
γ ≈ 0,577 215 664 901 532 860 606
Que é obtido fazendo o seguinte cálculo:
γ ≈ 1 + ½ + ⅓ + ¼ +… + 1 / n - ln (n)
Para quando n ser muito, muito grande. Para ter o valor exato do número Gama, você precisaria fazer o cálculo com n infinito. Algo semelhante ao que fizemos acima.
E existem muitos mais números transcendentes. O grande matemático Georg Cantor, nascido na Rússia e que viveu entre 1845 e 1918, mostrou que o conjunto dos números transcendentes é muito maior do que o conjunto dos números algébricos.
Fórmulas onde o número transcendente π aparece
O perímetro da circunferência
P = π D = 2 π R, onde P é o perímetro, D o diâmetro e R o raio da circunferência. Deve ser lembrado que:
-O diâmetro da circunferência é o segmento mais longo que une dois pontos da mesma e que sempre passa pelo seu centro,
-O raio é a metade do diâmetro e é o segmento que vai do centro até a borda.
Área de um círculo
A = π Rdois = ¼ π Ddois
Superfície de uma esfera
S = 4 π Rdois.
Sim. Embora possa não parecer, a superfície de uma esfera é a mesma de quatro círculos do mesmo raio da esfera..
Volume da esfera
V = 4/3 π R3
Treinamento
- Exercício 1
A pizzaria EXÓTICA vende pizzas de três diâmetros: pequenas 30 cm, médias 37 cm e grandes 45 cm. Uma criança está com muita fome e percebeu que duas pizzas pequenas custam o mesmo que uma grande. O que será melhor para ele, compre duas pizzas pequenas ou uma grande?

Solução
Quanto maior for a área, maior será a quantidade de pizza, por isso a área de uma pizza grande será calculada e comparada com a de duas pizzas pequenas:
Grande área de pizza = ¼ π Ddois = ¼ ⋅3,1416⋅45dois = 1590,44 cmdois
Pequena área de pizza = ¼ π ddois = ¼ ⋅3,1416⋅30dois = 706,86 cmdois
Portanto, duas pizzas pequenas terão uma área de
2 x 706,86 = 1413,72 cmdois .
É claro: você terá mais pizza comprando uma única grande do que duas pequenas.
- Exercício 2
A pizzaria “EXÓTICA” vende também uma pizza hemisférica com raio de 30 cm pelo mesmo preço de uma de formato retangular com uma lateral de 30 x 40 cm. Qual você escolheria?

Solução
Conforme mencionado na seção anterior, a área da superfície de uma esfera é quatro vezes maior que a de um círculo do mesmo diâmetro, portanto, um hemisfério de 30 cm de diâmetro terá:
Pizza hemisférica 12 '': 1413,72 cmdois (duas vezes uma circular do mesmo diâmetro)
Pizza retangular: (30 cm) x (40 cm) = 1200 cmdois .
A pizza hemisférica tem uma área maior.
Referências
- Fernández J. O número e. Origem e curiosidades. Recuperado de: soymatematicas.com
- Desfrute de matemática. Número de Euler. Recuperado de: gustolasmatematicas.com.
- Figuera, J. 2000. Mathematics 1st. Diversificado. Edições CO-BO.
- García, M. O número e no cálculo elementar. Recuperado de: matematica.ciens.ucv.ve.
- Wikipedia. Número PI. Recuperado de: wikipedia.com
- Wikipedia. Números transcendentes. Recuperado de: wikipedia.com


Ainda sem comentários