
Características da onda senoidal, peças, cálculo, exemplos
As ondas senoidais Eles são padrões de onda que podem ser descritos matematicamente pelas funções seno e cosseno. Eles descrevem com precisão eventos naturais e sinais que variam no tempo, como tensões geradas por usinas de energia e usadas em residências, indústrias e ruas.
Elementos elétricos como resistores, capacitores e indutâncias, que são conectados a entradas de tensão senoidal, também produzem respostas senoidais. A matemática usada em sua descrição é relativamente direta e foi exaustivamente estudada..

A matemática das ondas seno ou senoidal, como também são conhecidas, é a das funções seno e cosseno.
Essas são funções repetitivas, o que significa periodicidade. Ambos têm a mesma forma, exceto que o cosseno é deslocado para a esquerda em relação ao seno em um quarto de ciclo. Pode ser visto na figura 2:

Então cos x = sin (x + π / 2). Com a ajuda dessas funções, uma onda senoidal é representada. Para isso, a magnitude em questão é colocada no eixo vertical, enquanto o tempo está localizado no eixo horizontal..
O gráfico acima também mostra a qualidade repetitiva dessas funções: o padrão se repete contínua e regularmente. Graças a essas funções, é possível expressar tensões e correntes sinusoidais variando no tempo, posicionando-as no eixo vertical em vez do Y, uma v ou um eu para representar tensão ou corrente, e no eixo horizontal em vez do x, a t do tempo.
A maneira mais geral de expressar uma onda senoidal é:
v (t) = vm sen (ωt + φ)
Em seguida, vamos nos aprofundar no significado desta expressão, definindo alguns termos básicos para caracterizar a onda senoidal.
Índice do artigo
- 1 partes
- 1.1 Período
- 1.2 Amplitude
- 1.3 Ciclo
- 1.4 Freqüência
- 1.5 Fase
- 2 gerador de onda senoidal
- 2.1 Aplicação da lei de Faraday
- 2.2 Oscilador de Wien
- 3 Como calcular ondas senoidais?
- 3.1 O osciloscópio
- 4 exemplos
- 4.1 Exemplo 1
- 4.2 Exemplo 2
- 5 referências
Peças
Período, amplitude, frequência, ciclo e fase são conceitos aplicados a ondas periódicas ou repetitivas e são importantes para caracterizá-las adequadamente..
Período
Uma função periódica como as mencionadas, que se repete em intervalos regulares, sempre cumpre a seguinte propriedade:
f (t) = f (t + T) = f (t + 2T) = f (t + 3T) = ... .
Onde T é uma quantidade chamada período de onda, y é o tempo que leva para repetir uma fase do mesmo. Em unidades do Sistema Internacional, o período é medido em segundos.
Amplitude
De acordo com a expressão geral da onda senoidal v (t) = vm sin (ωt + φ), vm é o valor máximo da função, que ocorre quando sin (ωt + φ) = 1 (lembrando que o maior valor que as funções seno e cosseno admitem é 1). Este valor máximo é precisamente o amplitude de onda, também conhecido como amplitude de pico.
No caso de uma tensão será medida em Volts e se for uma corrente será em Amps. Na onda senoidal mostrada, a amplitude é constante, mas em outros tipos de onda a amplitude pode variar.
Ciclo
É uma parte da onda contida em um período. Na figura anterior, o período foi tomado medindo-o a partir de dois picos ou cristas consecutivos, mas pode começar a ser medido a partir de outros pontos da onda, desde que sejam limitados por um período.
Observe na figura a seguir como um ciclo percorre de um ponto a outro com o mesmo valor (altura) e a mesma inclinação (inclinação).
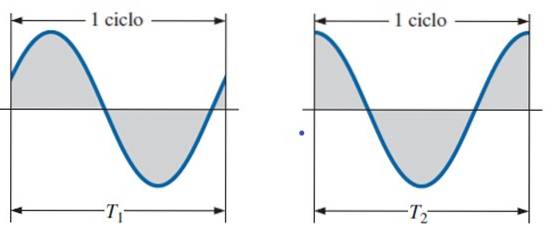
Frequência
É o número de ciclos que ocorrem em 1 segundo e está vinculado ao argumento da função seno: ωt. A frequência é indicada como F e é medido em ciclos por segundo ou Hertz (Hz) no Sistema Internacional.
A frequência é o valor inverso do período, portanto:
f = 1 / T
Enquanto a frequência F está relacionado a frequência angular ω (pulsação), como:
ω = 2πF
A frequência angular é expressa em radianos / segundo no Sistema Internacional, mas os radianos são adimensionais, então a frequência F e a frequência angular ω eles têm as mesmas dimensões. Observe que o produto ωt dá radianos como resultado e deve ser levado em consideração ao usar a calculadora para obter o valor de sen ωt.
Estágio
Corresponde ao deslocamento horizontal experimentado pela onda, em relação a um tempo tomado como referência.
Na figura a seguir, a onda verde está à frente da onda vermelha uma vez td. Duas ondas senoidais estão em Estágio quando sua frequência e fase são iguais. Se a fase for diferente, então eles estão em Gap = Vão. As ondas na figura 2 também estão fora de fase.
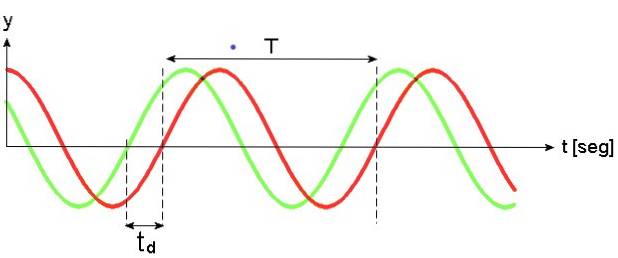
Se a frequência das ondas for diferente, elas estarão em fase quando a fase ωt + φ é o mesmo em ambas as ondas em certos momentos.
Gerador de onda senoidal
Existem muitas maneiras de obter um sinal de onda senoidal. Os soquetes domésticos fornecem-lhes.
Polícia de Faraday
Uma maneira bastante simples de obter um sinal senoidal é usar a lei de Faraday. Isso indica que em um circuito de corrente fechado, por exemplo um loop, colocado no meio de um campo magnético, uma corrente induzida é gerada quando o fluxo do campo magnético através dele muda no tempo. Consequentemente, um tensão induzida ou fem induzida.
O fluxo do campo magnético varia se o loop for girado com velocidade angular constante no meio do campo criado entre os pólos N e S do ímã mostrado na figura..
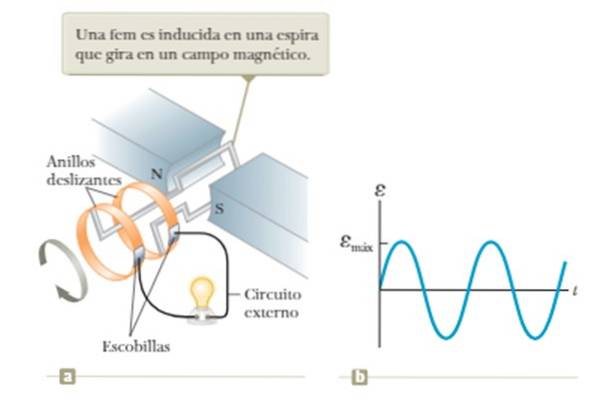
A limitação deste dispositivo é a dependência da tensão obtida com a frequência de rotação do loop, como será visto em maiores detalhes no Exemplo 1 da seção de Exemplos a seguir..
Oscilador de Wien
Outra forma de obter uma onda senoidal, desta vez com eletrônica, é por meio do oscilador de Wien, que requer um amplificador operacional em conexão com resistores e capacitores. Desta forma, são obtidas ondas senoidais cuja frequência e amplitude o usuário pode modificar de acordo com sua conveniência, ajustando com interruptores..
A figura mostra um gerador de sinais senoidais, com o qual também podem ser obtidas outras formas de onda: triangular e quadrada, entre outras..

Como calcular ondas senoidais?
Para realizar cálculos envolvendo ondas senoidais, é utilizada uma calculadora científica que possui as funções trigonométricas seno e cosseno, bem como suas inversas. Essas calculadoras têm modos de trabalhar os ângulos em graus ou radianos, e é fácil converter de uma forma para a outra. O fator de conversão é:
180 º = π radianos.
Dependendo do modelo da calculadora, você deve navegar usando a tecla MODE para encontrar a opção DEGREE, que permite trabalhar as funções trigonométricas em graus, ou a opção RAD, para trabalhar diretamente os ângulos em radianos.
Por exemplo sin 25º = 0,4226 com a calculadora configurada para o modo DEG. Converter 25º em radianos resulta em 0,4363 radianos e sen 0,4363 rad = 0,425889 ≈ 0,4226.
O osciloscópio
O osciloscópio é um dispositivo que permite a exibição de sinais de tensão e corrente diretos e alternados em uma tela. Possui botões para ajustar o tamanho do sinal em uma grade, conforme mostrado na figura a seguir:
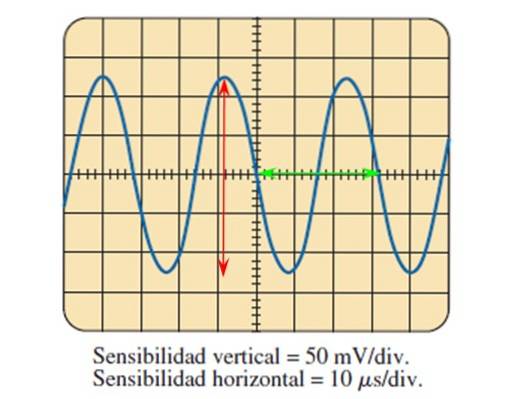
Através da imagem fornecida pelo osciloscópio e conhecendo o ajuste de sensibilidade em ambos os eixos, é possível calcular os parâmetros de onda que foram descritos anteriormente..
A figura mostra o sinal de tensão senoidal em função do tempo, em que cada divisão no eixo vertical vale 50 milivolts, enquanto no eixo horizontal cada divisão vale 10 microssegundos.
A amplitude de pico a pico é encontrada contando as divisões que a onda cobre verticalmente, usando a seta vermelha:
5 divisões são contadas com a ajuda da seta vermelha, então a tensão de pico a pico é:
Vpp = 5 divisões x 50 mV / divisão = 250 mV.
Tensão de pico Vp é medido a partir do eixo horizontal, sendo 125 mV.
Para encontrar o período, um ciclo é medido, por exemplo aquele delimitado pela seta verde, que cobre 3,2 divisões, então o período é:
T = 3,2 divisões x 10 microssegundos / divisão = 32 microssegundos = 32 μs
Exemplos
Exemplo 1
Para o gerador da Fig. 3, mostre a partir da lei de Faraday que a tensão induzida tem uma forma senoidal. Suponha que o loop consiste em N voltas em vez de apenas uma, todas com a mesma área A e está girando com velocidade angular constante ω no meio de um campo magnético B uniforme.
Solução
A lei de Faraday diz que a fem induzida ε isso é:
ε = -N (dΦB / dt)
Onde ΦB é o fluxo do campo magnético, que será variável, pois depende de como o loop é exposto ao campo a cada momento. O sinal negativo descreve simplesmente o fato de que esta fem se opõe à causa que a produz (lei de Lenz). O fluxo devido a uma única volta é:
ΦB = B.A.cos θ
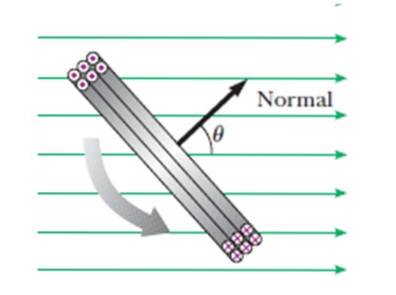
θ é o ângulo que o vetor normal ao plano do loop forma com o campo B Conforme a rotação prossegue (veja a figura), este ângulo naturalmente varia como:
θ = ωt
De maneira que: ΦB = B.A.cos θ = B.A.cos ωt. Agora só temos que derivar esta expressão com respeito ao tempo e com isso obtemos a fem induzida:
ε = -N.d (B.A.cos ωt) / dt
Como o campo B é uniforme e a área do loop não varia, eles saem de fora da derivada:
ε = -NBA. d (cos ωt) / dt = ωNBA. sen ωt
Exemplo 2
Um loop tem uma área de 0,100 mdois e gira a 60,0 rev / s, com seu eixo de rotação perpendicular a um campo magnético uniforme de 0,200 T. Sabendo que a bobina tem 1000 voltas, encontre: a) A fem máxima que é gerada, b) A orientação da bobina em relação com o campo magnético quando ocorre a fem máxima induzida.
Solução
a) A fem máxima é εmax = ωNBA
Antes de proceder à substituição dos valores, a frequência de 60 rev / s deve ser transferida para as unidades do Sistema Internacional. Sabe-se que 1 revolução é igual a uma revolução ou 2 radianos:
60,0 rev / s = 120p radianos / s
εmax = 120p radianos x 1000 voltas x 0,200 T x 0,100 mdois = 7539,82 V = 7,5 kV
b) Quando este valor ocorre sen ωt = 1 portanto:
ωt = θ = 90º,
Nesse caso, o plano da espiral é paralelo a B, de modo que o vetor normal ao referido plano forme 90º com o campo. Isso ocorre quando o vetor em preto na figura 8 é perpendicular ao vetor verde que representa o campo magnético.
Referências
- Boylestad, R. 2011. Introdução à análise de circuitos. 12º. Edição. Pearson. 327-376.
- Figueroa, D. 2005. Electromagnetism. Série de Física para Ciência e Engenharia. Volume 6. Editado por D. Figueroa. Universidade Simon Bolivar. 115 e 244-245.
- Figueroa, D. 2006. Laboratório de Física 2. Editorial Equinoccio. 03-1 e 14-1.
- Ondas senoidais. Recuperado de: iessierradeguara.com
- Serway, R. 2008. Física para Ciência e Engenharia. Volume 2. Cengage Learning. 881-884



Ainda sem comentários