
Expressão matemática e exemplos de ondas unidimensionais
As ondas unidimensionais Eles são aqueles que se propagam em uma única direção, independentemente de a vibração ocorrer na mesma direção de propagação ou não. Um bom exemplo deles é a onda que percorre uma corda esticada como a de um violão..
Em uma onda plana Cruz, as partículas vibram na direção vertical (vão para cima e para baixo, veja a seta vermelha na figura 1), mas é unidimensional porque a perturbação viaja em apenas uma direção, seguindo a seta amarela.

As ondas unidimensionais aparecem com bastante frequência na vida cotidiana. A seção a seguir descreve alguns exemplos deles e também de ondas que não são unidimensionais, para estabelecer claramente as diferenças.
Índice do artigo
- 1 Exemplos de ondas unidimensionais e ondas não unidimensionais
- 1.1 Ondas unidimensionais
- 1.2 Ondas não unidimensionais
- 2 Expressão matemática de uma onda unidimensional
- 2.1 Equação de onda unidimensional
- 2.2 Exemplo trabalhado
- 3 referências
Exemplos de ondas unidimensionais e ondas não unidimensionais
Ondas unidimensionais
Aqui estão alguns exemplos de ondas unidimensionais que podem ser facilmente observadas:
- Um pulso de som que percorre uma barra reta, pois é um distúrbio que se propaga por toda a extensão da barra..
- Uma onda viajando por um canal de água, embora o deslocamento da superfície da água não seja paralelo ao canal.
- Ondas que se propagam em uma superfície ou através do espaço tridimensional também podem ser unidimensionais, desde que suas frentes de onda sejam planos paralelos entre si e viajem em apenas uma direção..
Ondas não unidimensionais
Um exemplo de onda não unidimensional é encontrado em ondas que se formam em uma superfície de água parada quando uma pedra cai. É uma onda bidimensional com uma frente de onda cilíndrica.

Outro exemplo de onda não unidimensional é a onda sonora que um foguete gera ao explodir em uma determinada altura. Esta é uma onda tridimensional com frentes de onda esféricas.
Expressão matemática de uma onda unidimensional
A forma mais geral de expressar uma onda unidimensional que se propaga sem atenuação na direção positiva do eixo x e com velocidade v é, matematicamente:
y (x, t) = f (x - v.t)
Nesta expressão Y representa a perturbação na posição x no momento t. A forma da onda é dada pela função F. Por exemplo, a função de onda mostrada na figura 1 é: y (x, t) = cos (x - v t) e a imagem da onda corresponde ao instante t = 0.
Uma onda como esta, descrita por uma função cosseno ou seno, é chamada onda harmônica. Embora não seja a única forma de onda existente, é de extrema importância, pois qualquer outra onda pode ser representada como uma superposição ou soma de ondas harmônicas. É sobre o conhecido Teorema de Fourier, tão usado para descrever sinais de todos os tipos.
Quando a onda viaja na direção negativa do eixo x, ela simplesmente muda v para -v no argumento, deixando:
y (x, t) = g (x + v t)
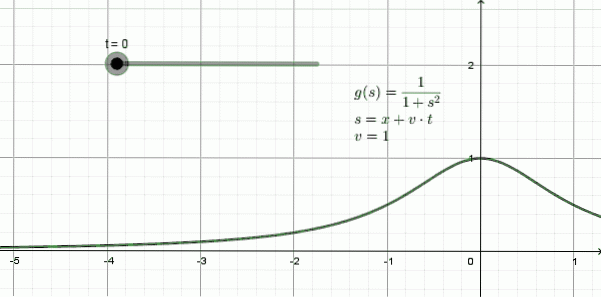
A Figura 3 mostra a animação de uma onda viajando para a esquerda: é uma forma chamada de função Lorentziana e ela expressão matemática é:
y (x, t) = 1 / (1 + (x + 1⋅t)dois
Neste exemplo, a velocidade de propagação é v = 1, -uma unidade de espaço para cada unidade de tempo-.
Equação de onda unidimensional
A equação da onda é uma equação derivada parcial, a solução da qual é, obviamente, uma onda. Estabelece a relação matemática entre a parte espacial e a parte temporal dela, e tem a forma:

Exemplo trabalhado
A seguir está a expressão geral y (x, t) para uma onda harmônica:
y (x, t) = A⋅cos (k⋅x ± ω⋅t + θo)
a) Descreva o significado físico dos parâmetros A, k, ω Y θo.
b) Qual o significado dos sinais ± têm no argumento do cosseno?
c) Verifique se a expressão dada é de fato a solução da equação de onda da seção anterior e encontre a velocidade v propagação.
Solução para)
As características da onda são encontradas nos seguintes parâmetros:
-PARA representa o amplitude ou "altura da onda".
-o que está em número de onda e está relacionado ao comprimento de onda λ Através dos k = 2π / λ.
-ω é o ffrequência angular e está relacionado ao período T oscilação de onda por
ω = 2π / T.
-θo é o fase inicial, que está relacionado ao ponto de partida da onda.
Solução b)
Um sinal negativo é assumido se a onda viaja na direção positiva do eixo X e um sinal positivo caso contrário..
Solução c)
Verifique se a expressão dada é uma solução da equação de onda é simples: a derivada parcial da função é tomada y (x, t) com respeito ax duas vezes, derivada parcialmente em relação a t duas vezes e, em seguida, combine os dois resultados para obter uma igualdade:
Segunda derivada em relação ax: ∂doisy / ∂xdois= -Kdois. PARA⋅cos (k⋅x ± ω⋅t + θo)
Segunda derivada em relação a t: ∂doisy / ∂tdois= -Ωdois. PARA⋅cos (k⋅x ± ω⋅t + θo)
Esses resultados são substituídos na equação de onda:
-kdois. PARA⋅cos (k⋅x ± ω⋅t + θo) = (1 / vdois) (-ωdois. PARA⋅cos (k⋅x ± ω⋅t + θo))
Muito PARA como os cossenos são simplificados, uma vez que aparecem em ambos os lados da igualdade e o argumento do cosseno é o mesmo, portanto a expressão se reduz a:
-kdois = (1 / vdois) (-ωdois)
O que permite obter uma equação para v em termos de ω Y k:
vdois = ωdois / kdois
v = ± ω / k
Referências
- E-educacional. Equação de ondas harmônicas unidimensionais. Recuperado de: e-ducativa.catedu.es
- O canto da Física. Aulas de ondas. Recuperado de: fisicaparatontos.blogspot.com.
- Figueroa, D. 2006. Waves and Quantum Physics. Série: Física para Ciência e Engenharia. Editado por Douglas Figueroa. Universidade Simon Bolivar. Caracas Venezuela.
- Laboratório de Física. Movimento ondulatório. Recuperado de: fisicalab.com.
- Peirce, A. Aula 21: A Equação de Onda unidimensional: Solução de D'Alembert. Recuperado de: ubc.ca.
- Equação de onda. Recuperado de: en.wikipedia.com



Ainda sem comentários