
Fórmulas de ortoedro, área, volume, diagonal, exemplos
O ortoedro É uma figura geométrica volumétrica ou tridimensional que se caracteriza por ter seis faces retangulares, de forma que as faces opostas estão em planos paralelos e são retângulos idênticos ou congruentes. Por outro lado, as faces adjacentes a uma dada face estão em planos perpendiculares ao da face inicial..
Também pode ser considerado ortoedro como um prisma ortogonal com uma base retangular, em que o ângulos diédricos formados pelos planos de duas faces adjacentes a uma aresta comum, medem 90º. O ângulo diedro entre duas faces é medido na interseção das faces com um plano perpendicular comum a elas.
Da mesma forma, o ortoedro é um retângulo paralelepípedo, pois é assim que o paralelepípedo é definido como a figura volumétrica de seis faces, que são paralelas duas a duas.
Em qualquer paralelepípedo as faces são paralelogramos, mas no paralelepípedo retangular as faces devem ser retangulares.
Índice do artigo
- 1 partes do ortoedro
- 2 fórmulas do ortoedro
- 2.1 Área
- 2.2 Volume
- 2.3 diagonal interna
- 3 exemplos
- 3.1 - Exemplo 1
- 3.2 - Exercício 2
- 4 referências
Partes do ortoedro
As partes de um poliedro, como o ortoedro, Eles são:
-Arestas
-Vértices
-Rostos
O ângulo entre duas arestas de uma face do ortoedro coincide com o ângulo diedro formado por suas outras duas faces adjacentes a cada uma das arestas, formando um ângulo reto. A imagem a seguir esclarece cada conceito:
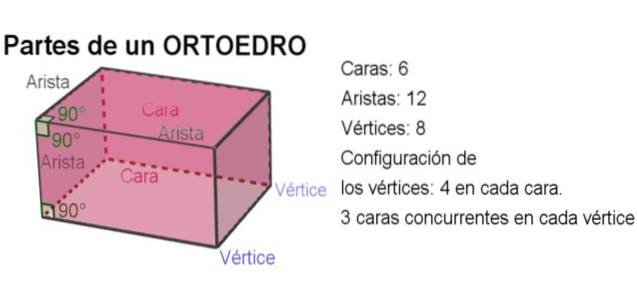
-No total, um ortoedro tem 6 faces, 12 arestas e 8 vértices..
-O ângulo entre quaisquer duas arestas é um ângulo reto.
-O ângulo diedro entre quaisquer duas faces também está correto.
-Em cada face existem quatro vértices e em cada vértice três faces mutuamente ortogonais coincidem.
Fórmulas de ortoedro
Área
A superfície ou área de um ortoedro é a soma das áreas de seus rostos.
Se as três arestas que se encontram em um vértice têm medidas a, b e c, como mostrado na Figura 3, então a face frontal tem área c⋅b e a face inferior também tem área c⋅b.
Então, as duas faces laterais têm área a⋅b cada uma. E, por último, as faces do piso e do teto têm área AC cada uma.
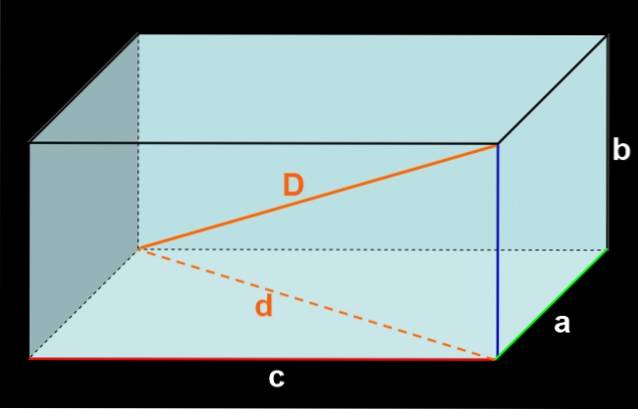
Adicionar a área de todos os rostos dá:
A = 2⋅c⋅b + 2⋅a⋅b + 2⋅a⋅c
Pegando um fator comum e ordenando os termos:
A = 2⋅ (a⋅b + b⋅c + c⋅a)
Volume
Se o ortoedro é pensado como um prisma, então seu volume é calculado da seguinte forma:
Volume = Área da base do prisma x altura do prisma
Neste caso, o piso de dimensões é tomado como base retangular c Y para, então a área da base é c⋅a.
A altura é dada pelo comprimento b das bordas ortogonais às faces laterais para Y c.
Multiplicando a área da base (AC) por altura b você tem o volume V do ortoedro:
V = a⋅b⋅c
Diagonal interna
Em um ortoedro, existem dois tipos de diagonais: as diagonais externas e as diagonais internas.
As diagonais externas estão nas faces retangulares, enquanto as diagonais internas são os segmentos que unem dois vértices opostos, sendo entendidos por vértices opostos aqueles que não compartilham nenhuma aresta..
Em um ortoedro, existem quatro diagonais internas, todas de igual medida. O comprimento das diagonais internas pode ser obtido aplicando o teorema de Pitágoras para triângulos retângulos.
O comprimento d da diagonal externa da face do piso do ortoedro cumpre a relação pitagórica:
ddois = adois + cdois
Da mesma forma, a diagonal interna da medida D cumpre a relação pitagórica:
Ddois = ddois + bdois.
Combinando as duas expressões anteriores, temos:
Ddois = adois + cdois + bdois.
Finalmente, o comprimento de qualquer uma das diagonais internas do ortoedro é dado pela seguinte fórmula:
D = √ (adois + bdois + cdois ).
Exemplos
- Exemplo 1
Um pedreiro constrói um tanque em forma de ortoedro cujas dimensões internas são: 6 m x 4 m de base e 2 m de altura. Ele pergunta:
a) Determine a superfície interna do tanque se ele estiver completamente aberto na parte superior.
b) Calcule o volume do espaço interior do tanque.
c) Encontre o comprimento de uma diagonal interna.
d) Qual a capacidade do tanque em litros?
Solução para
Tomaremos as dimensões da base retangular a = 4 me c = 6 m e a altura como b = 2 m
A área de um ortoedro com as dimensões fornecidas é dada pela seguinte relação:
A = 2⋅ (a⋅b + b⋅c + c⋅a) = 2⋅ (4 m⋅2 m + 2 m⋅6 m + 6 m⋅4 m)
Quer dizer:
A = 2⋅ (8 mdois + 12 mdois + 24 mdois) = 2⋅ (44 mdois) = 88 mdois
O resultado anterior é a área do ortoedro fechado com as dimensões dadas, mas por se tratar de um tanque completamente descoberto em sua parte superior, para se obter na superfície das paredes internas do tanque, a área da tampa que falta deve ser subtraído, que é:
c⋅a = 6 m ⋅ 4 m = 24 mdois.
Finalmente, a superfície interna do tanque será: S = 88 mdois - 24 mdois = 64 mdois.
Solução b
O volume interno do tanque é dado pelo volume de um ortoedro das dimensões internas do tanque:
V = a⋅b⋅c = 4 m ⋅ 2 m ⋅ 6 m = 48 m3.
Solução c
A diagonal interna de um octaedro com as dimensões do interior do tanque tem um comprimento D dado por:
√ (paradois + bdois + cdois ) = √ ((4 m)dois + (2 m)dois + (6 m)dois )
Realizando as operações indicadas temos:
D = √ (16 mdois + 4 mdois + 36 mdois ) = √ (56 mdois) = 2√ (14) m = 7,48 m.
Solução d
Para calcular a capacidade do tanque em litros, é necessário saber que o volume de um decímetro cúbico é igual à capacidade de um litro. Anteriormente, havia sido calculado em volume em metros cúbicos, mas deve ser transformado em decímetros cúbicos e depois em litros:
V = 48 m3 = 48 (10 dm)3 = 4.800 dm3 = 4.800 L
- Exercício 2
Um aquário de vidro tem uma forma cúbica com 25 cm de lado. Determine a área em mdois, o volume em litros e o comprimento de uma diagonal interna em cm.
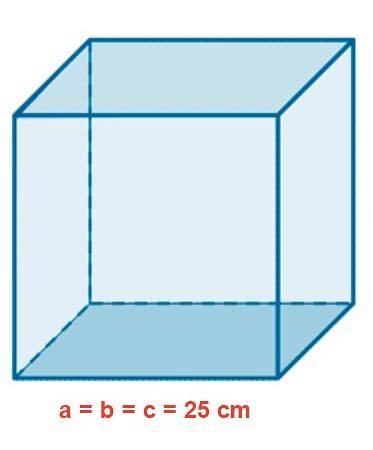
Solução
A área é calculada usando a mesma fórmula de ortoedro, mas levando em consideração que todas as dimensões são idênticas:
A = 2⋅ (3 a⋅a) = 6⋅ adois = 6⋅ (25 cm)dois = 1.250 cmdois
O volume do cubo é dado por:
V = a3 = (25 cm)3 = 15,625 cm3 = 15.625 (0,1 dm)3 = 15.625 dm3 = 15,625 L.
O comprimento D da diagonal interna é:
D = √ (3adois) = 25√ (3) cm = 43,30 cm.
Referências
- Arias J. GeoGebra: Prism. Recuperado de: youtube.com.
- Calculus.cc. Exercícios e resolução de problemas de áreas e volumes. Recuperado de: calculo.cc.
- Salvador R. Pirâmide + ortoedro com GEOGEBRA (IHM). Recuperado de: youtube.com
- Weisstein, Eric. "Ortoedro". MathWorld. Wolfram Research.
- Wikipedia. Ortoedro Recuperado de: es.wikipedia.com



Ainda sem comentários