
Papomudas Como resolvê-los e exercícios
O papomudas é um procedimento para resolver expressões algébricas. Suas siglas indicam a ordem de prioridade das operações: parênteses, potências, multiplicação, divisão, adição e subtração. Usando esta palavra você pode facilmente lembrar a ordem em que você deve resolver uma expressão composta de várias operações.
Geralmente, em expressões numéricas, várias operações aritméticas podem ser encontradas juntas, como adição, subtração, multiplicação e divisão, que também podem ser frações, potências e raízes. Para resolvê-los, é necessário seguir um procedimento que garanta que os resultados serão corretos..

Uma expressão aritmética composta por uma combinação dessas operações deve ser resolvida de acordo com a ordem de prioridade, também conhecida como hierarquia de operações, estabelecida há muito tempo em convenções universais. Assim, todas as pessoas podem seguir o mesmo procedimento e obter o mesmo resultado.
Índice do artigo
- 1 recursos
- 2 Como resolvê-los?
- 3 aplicativo
- 3.1 Expressões contendo adição e subtração
- 3.2 Expressões contendo adição, subtração e multiplicação
- 3.3 Expressões contendo adição, subtração, multiplicação e divisão
- 3.4 Expressões contendo adição, subtração, multiplicação, divisão e potências
- 3.5 Expressões que usam símbolos de agrupamento
- 4 exercícios
- 4.1 Primeiro exercício
- 4.2 Segundo exercício
- 4.3 Terceiro exercício
- 5 referências
Caracteristicas
Papomudas é um procedimento padrão que estabelece a ordem que deve ser seguida na resolução de uma expressão, que é composta por uma combinação de operações como adição, subtração, multiplicação e divisão..
Com este procedimento, a ordem de prioridade de uma operação é estabelecida em relação às demais no momento em que serão resultados; ou seja, cada operação tem um turno ou nível hierárquico a ser resolvido.
A ordem em que as diferentes operações de uma expressão devem ser resolvidas é dada por cada acrônimo da palavra papomudas. Assim, você deve:
1- Pa: parênteses, colchetes ou colchetes.
2- Po: poderes e raízes.
3- Mu: multiplicações.
4- D: divisões.
5- A: adições ou adições.
6- S: subtrações ou subtrações.
Este procedimento também é denominado em inglês como PEMDAS; para lembrar facilmente esta palavra está associada à frase: "Pleitura Excuse MY Dorelha PARAunt Saliado”, Onde cada letra inicial corresponde a uma operação aritmética, da mesma forma que os papomudas.
Como resolvê-los?
Com base na hierarquia estabelecida pelos papomudas para resolver as operações de uma expressão, é necessário cumprir a seguinte ordem:
- Todas as operações dentro de símbolos de agrupamento, como parênteses, colchetes, colchetes e barras de fração, devem primeiro ser resolvidas. Quando houver símbolos de agrupamento dentro de outros, você deve começar a calcular de dentro para fora.
Esses símbolos são usados para alterar a ordem em que as operações são resolvidas, pois o que está dentro deles deve sempre ser resolvido primeiro..
- Então os poderes e raízes são resolvidos.
- Em terceiro lugar, as multiplicações e divisões são resolvidas. Eles têm a mesma ordem de prioridade; portanto, quando essas duas operações são encontradas em uma expressão, a que aparece primeiro deve ser resolvida, lendo a expressão da esquerda para a direita.
- Por último, resolvem-se as adições e subtrações, que também têm a mesma ordem de prioridade e, portanto, resolve-se aquela que aparece primeiro na expressão lida da esquerda para a direita.
- As operações nunca devem ser misturadas quando lidas da esquerda para a direita, a ordem de prioridade ou hierarquia estabelecida pelos papomudas deve sempre ser seguida..
É importante lembrar que o resultado de cada operação deve ser colocado na mesma ordem em relação às demais, e todas as etapas intermediárias devem ser separadas por um sinal até que o resultado final seja alcançado..
Aplicativo
O procedimento papomudas é usado quando você tem uma combinação de diferentes operações. Levando em consideração como são resolvidos, isso pode ser aplicado em:
Expressões contendo adição e subtração
É uma das operações mais simples, pois ambas têm a mesma ordem de prioridade, de forma que deve ser resolvida a partir da esquerda para a direita na expressão; por exemplo:
22 -15 + 8 +6 = 21.
Expressões contendo adição, subtração e multiplicação
Nesse caso, a operação de maior prioridade é a multiplicação, então a adição e a subtração são resolvidas (o que ocorrer primeiro na expressão). Por exemplo:
6 * 4 - 10 + 8 * 6 - 16 + 10 * 6
= 24 -10 + 48 - 16 + 60
= 106.
Expressões contendo adição, subtração, multiplicação e divisão
Neste caso, você tem uma combinação de todas as operações. Você começa resolvendo a multiplicação e divisão que têm maior prioridade, depois a adição e subtração. Lendo a expressão da esquerda para a direita, ela é resolvida de acordo com sua hierarquia e posição dentro da expressão; por exemplo:
7 + 10 * 13 - 8 + 40 ÷ 2
= 7 + 130 - 8 + 20
= 149.
Expressões contendo adição, subtração, multiplicação, divisão e potências
Neste caso, um dos números é elevado a uma potência, que dentro do nível de prioridade deve ser resolvido primeiro, para depois resolver as multiplicações e divisões, e finalmente as adições e subtrações:
4 + 4dois * 12 - 5 + 90 ÷ 3
= 4 + 16 * 12 - 5 + 90 ÷ 3
= 4 + 192 - 5 + 30
= 221.
Como os poderes, as raízes também têm a segunda ordem de prioridade; Portanto, em expressões que os contêm, multiplicação, divisão, adição e subtração devem ser resolvidas primeiro:
5 * 8 + 20 ÷ √16
= 5 * 8 + 20 ÷ 4
= 40 + 5
= 45.
Expressões que usam símbolos de agrupamento
Quando sinais como parênteses, colchetes, colchetes e barras de fração são usados, o que está dentro deles é resolvido primeiro, independentemente da ordem de prioridade das operações que contenha em relação às que estão fora, como se fosse uma expressão separada :
14 ÷ 2 - (8 - 5)
= 14 ÷ 2 - 3
= 7 - 3
= 4.
Se houver várias operações dentro dele, elas devem ser resolvidas em ordem hierárquica. Em seguida, as outras operações que compõem a expressão são resolvidas; por exemplo:
2 + 9 * (5 + 23 - 24 ÷ 6) - 1
= 2 + 9 * (5 + 8 - 4) - 1
= 2 + 9 * 9 - 1
= 2 + 81 - 1
= 82.
Algumas expressões usam símbolos de agrupamento dentro de outras, como quando é necessário alterar o sinal de uma operação. Nesses casos, você deve começar resolvendo de dentro para fora; ou seja, simplificando os símbolos de agrupamento que estão no centro de uma expressão.
Geralmente, a ordem para resolver as operações contidas nesses símbolos é: primeiro resolva o que está entre parênteses (), depois os colchetes [] e, por último, os colchetes .
90 - 3*[12 + (5*4) - (4*dois)]
= 90 - 3* [12 + 20 - 8]
= 90 - 3 * 24
= 90 - 72
= 18.
Treinamento
Primeiro exercício
Encontre o valor da seguinte expressão:
vintedois + √225 - 155 + 130.
Solução
Aplicando os papomudas, os poderes e raízes têm que ser resolvidos primeiro, e depois adição e subtração. Nesse caso, as duas primeiras operações pertencem à mesma ordem, então a que é a primeira é resolvida, começando da esquerda para a direita:
vintedois + √225 - 155 + 130
= 400 + 15 -155 + 130.
Então você adiciona e subtrai, começando da esquerda também:
400 + 15 -155 + 130
= 390.
Segundo exercício
Encontre o valor da seguinte expressão:
[- (63 - 36) ÷ (8 * 6 ÷ 16)].
Solução
Começa resolvendo as operações que estão entre parênteses, seguindo a ordem hierárquica que têm de acordo com os papomudas..
Primeiro, as potências dos primeiros parênteses são resolvidas, depois as operações dos segundos parênteses são resolvidas. Por pertencerem à mesma ordem, resolve-se a primeira operação da expressão:
[- (63 - 36) ÷ (8 * 6 ÷ 16)]
= [- (216 - 729) ÷ (8 * 6 ÷ 16)]
= [- (216 - 729) ÷ (48 ÷ 16)]
= [- (-513) ÷ (3)].
Como as operações entre parênteses já foram resolvidas, agora continuamos com a divisão que possui uma hierarquia superior à subtração:
[- (-513) ÷ (3)] = [- (-171)].
Por fim, o parêntese que separa o sinal de menos (-) do resultado, que neste caso é negativo, indica que esses sinais devem ser multiplicados. Assim, o resultado da expressão é:
[- (-171)] = 171.
Terceiro exercício
Encontre o valor da seguinte expressão:

Solução
Você começa resolvendo as frações que estão entre parênteses:
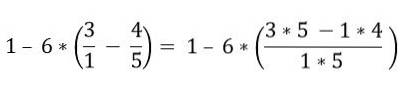
Dentro dos parênteses existem várias operações. As multiplicações são resolvidas primeiro e depois as subtrações; Neste caso, a barra de fração é considerada como um símbolo de agrupamento e não como uma divisão, por isso as operações da parte superior e inferior devem ser resolvidas:
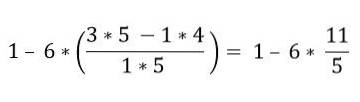
Em ordem hierárquica, a multiplicação deve ser resolvida:
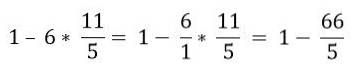
Finalmente, a subtração é resolvida:
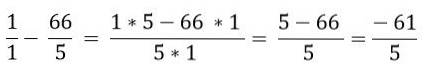
Referências
- Aguirre, H. M. (2012). Matemática financeira. Cengage Learning.
- Aponte, G. (1998). Fundamentos de matemática básica. Pearson Education.
- Cabanne, N. (2007). Didática da Matemática.
- Carolina Espinosa, C. C. (2012). Recursos em operações de aprendizagem.
- Huffstetler, K. (2016). A história da ordem de operações: Pemdas. Criar Espaço Independente .
- Madore, B. (2009). Livro de Matemática GRE. Série Educacional de Barron,.
- Molina, F. A. (s.f.). Projeto Azarquiel, Matemática: Primeiro ciclo. Grupo Azarquiel.



Ainda sem comentários