
Definição, propriedades e exemplos de parabolóide hiperbólico

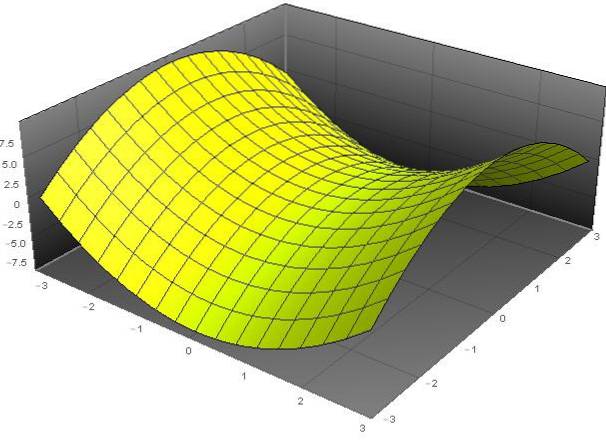
UMA parabolóide hiperbólico é uma superfície cuja equação geral em coordenadas cartesianas (x, y, z) cumpre a seguinte equação:
(para)dois - (e B)dois - z = 0.
O nome "parabolóide" vem do fato de que a variável z depende dos quadrados das variáveis x e y. Já o adjetivo "hiperbólico" se deve ao fato de que em valores fixos de z temos a equação de uma hipérbole. A forma desta superfície é semelhante à de uma sela de cavalo.
Índice do artigo
- 1 Descrição do parabolóide hiperbólico
- 2 Propriedades do parabolóide hiperbólico
- 3 exemplos trabalhados
- 3.1 - Exemplo 1
- 3.2 - Exemplo 2
- 3.3 - Exemplo 3
- 4 O parabolóide hiperbólico na arquitetura
- 5 referências
Descrição do parabolóide hiperbólico
Para entender a natureza do parabolóide hiperbólico, a seguinte análise será feita:
1.- Tomaremos o caso particular a = 1, b = 1, ou seja, a equação cartesiana do parabolóide permanece como z = xdois - Ydois.
2.- São considerados planos paralelos ao plano ZX, ou seja, y = ctte.
3.- Com y = ctte permanece z = xdois - C, que representam parábolas com ramos para cima e vértice abaixo do plano XY.
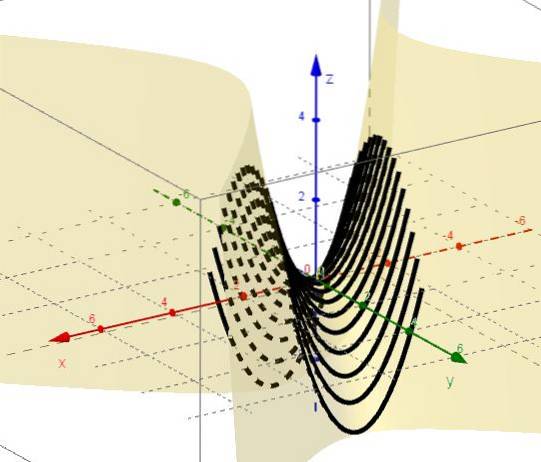
4.- Com x = ctte permanece z = C - ydois, que representam parábolas com ramificações para baixo e vértice acima do plano XY.
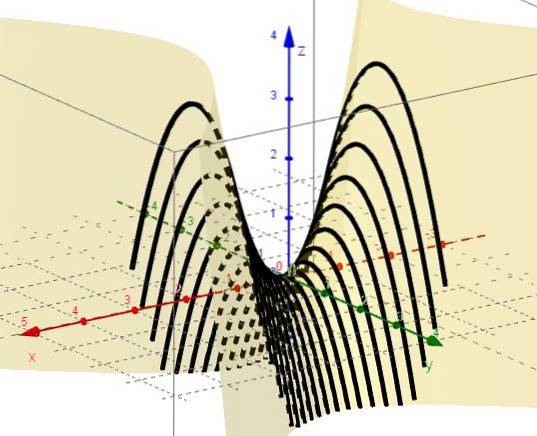
5.- Com z = ctte permanece C = xdois - Ydois, que representam hipérboles em planos paralelos ao plano XY. Quando C = 0, há duas linhas (em + 45º e -45º em relação ao eixo X) que se cruzam na origem no plano XY.
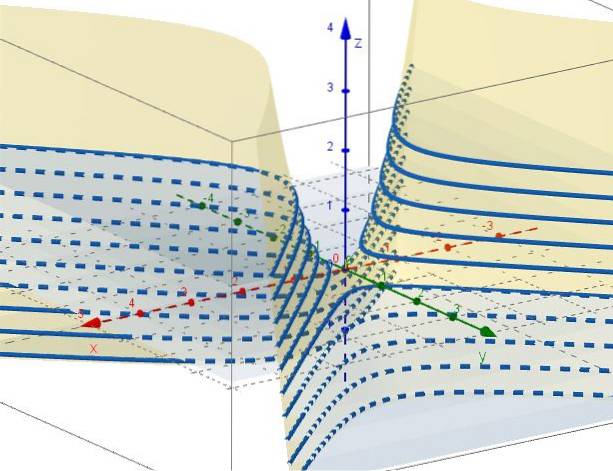
Propriedades do parabolóide hiperbólico
1.- Quatro pontos diferentes no espaço tridimensional definem um e apenas um parabolóide hiperbólico.
2.- O parabolóide hiperbólico é um superfície duplamente governada. Isso significa que, apesar de ser uma superfície curva, duas linhas diferentes passam por cada ponto de um parabolóide hiperbólico que pertence totalmente ao parabolóide hiperbólico. A outra superfície que não é um plano e é duplamente regida é a hiperbolóide de revolução.
É precisamente a segunda propriedade do parabolóide hiperbólico que tem permitido seu amplo uso na arquitetura, uma vez que a superfície pode ser gerada a partir de vigas ou cordas retas..
A segunda propriedade do parabolóide hiperbólico permite uma definição alternativa dele: é a superfície que pode ser gerada por uma linha reta móvel paralela a um plano fixo e corta duas linhas fixas que servem de guia. A figura a seguir esclarece esta definição alternativa do parabolóide hiperbólico:
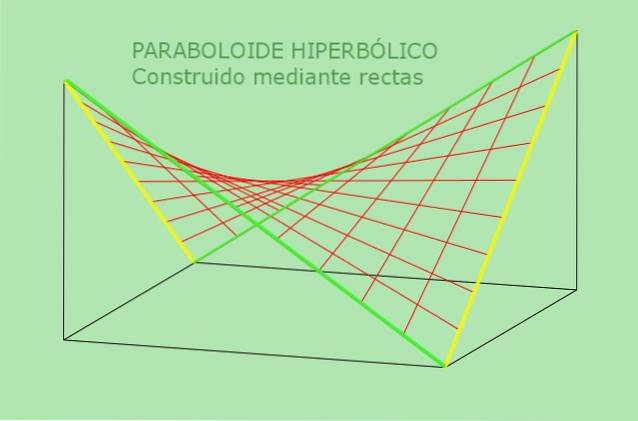
Exemplos trabalhados
- Exemplo 1
Mostre que a equação: z = xy, corresponde a um parabolóide hiperbólico.
Solução
Será aplicada uma transformação às variáveis xey correspondentes a uma rotação dos eixos cartesianos em relação ao eixo Z de + 45º. As antigas coordenadas x e y são transformadas nas novas x 'e y' de acordo com as seguintes relações:
x = x '- y'
y = x '+ y'
enquanto a coordenada z permanece a mesma, ou seja, z = z '.
Substituindo na equação z = x e temos:
z '= (x' - y ') (x' + y ')
Ao aplicar o produto notável da diferença pela soma igual à diferença dos quadrados, temos:
z '= x'dois - Y 'dois
que corresponde claramente à definição inicialmente dada de parabolóide hiperbólico.
A interceptação dos planos paralelos ao eixo XY com o parabolóide hiperbólico z = x e determinar hipérboles equiláteros que têm como assíntotas os planos x = 0 ey = 0.
- Exemplo 2
Determine os parâmetros para Y b do parabolóide hiperbólico que passa pelos pontos A (0, 0, 0); B (1, 1, 5/9); C (-2, 1, 32/9) e D (2, -1, 32/9).
Solução
De acordo com suas propriedades, quatro pontos no espaço tridimensional determinam um único parabolóide hiperbólico. A equação geral é:
z = (x / a)dois - (e B)dois
Substituímos os valores fornecidos:
Para o ponto A, temos 0 = (0 / a)dois - (0 / b)dois, equação que é satisfeita quaisquer que sejam os valores dos parâmetros a e b.
Substituindo o ponto B, obtemos:
5/9 = 1 / adois - 1 Bdois
Enquanto para o ponto C permanece:
32/9 = 4 / adois - 1 bilhãodois
Finalmente, para o ponto D, obtemos:
32/9 = 4 / adois - 1 Bdois
Que é idêntica à equação anterior. Em última análise, o sistema de equações deve ser resolvido:
5/9 = 1 / adois - 1 Bdois
32/9 = 4 / adois - 1 Bdois
Subtraindo a segunda equação da primeira resulta:
27/9 = 3 / adois o que implica que umdois = 1.
Da mesma forma, a segunda equação é subtraída do quádruplo da primeira, obtendo:
(32-20) / 9 = 4 / adois - 4 / adois -1 Bdois + 4 / bdois
Que é simplificado como:
12/9 = 3 / bdois ⇒ bdois = 9/4.
Em suma, o parabolóide hiperbólico que passa pelos pontos dados A, B, C e D tem uma equação cartesiana dada por:
z = xdois - (4/9) edois
- Exemplo 3
De acordo com as propriedades do parabolóide hiperbólico, duas linhas passam por cada ponto que está completamente contido nele. Para o caso z = x ^ 2 - y ^ 2 encontre a equação das duas retas que passam pelo ponto P (0, 1, -1) claramente pertencente ao parabolóide hiperbólico, de modo que todos os pontos dessas retas também pertencem para o mesmo.
Solução
Usando o notável produto da diferença de quadrados, a equação para o parabolóide hiperbólico pode ser escrita assim:
(x + y) (x - y) = c z (1 / c)
Onde c é uma constante diferente de zero.
A equação x + y = c z, e a equação x - y = 1 / c correspondem a dois planos com vetores normais n=<1,1,-c> Y m=<1,-1,0>. O produto vetorial m x n =<-c, -c, -2> nos dá a direção da linha de interseção dos dois planos. Então, uma das retas que passa pelo ponto P e pertence ao parabolóide hiperbólico tem uma equação paramétrica:
Para determinar c, substituímos o ponto P na equação x + y = c z, obtendo:
c = -1
De forma semelhante, mas considerando as equações (x - y = k z) e (x + y = 1 / k), temos a equação paramétrica da reta:
Em resumo, as duas linhas:
Eles estão completamente contidos no parabolóide hiperbólico z = xdois - Ydois passando pelo ponto (0, 1, -1).
Como verificação, suponha que t = 1, o que nos dá o ponto (1,2, -3) na primeira linha. Você tem que verificar se ele também está no parabolóide z = xdois - Ydois:
-3 = 1dois - doisdois = 1 - 4 = -3
O que confirma que ele realmente pertence à superfície do parabolóide hiperbólico.
O parabolóide hiperbólico na arquitetura

O parabolóide hiperbólico tem sido utilizado na arquitectura pelos grandes arquitectos de vanguarda, entre os quais se destacam os nomes do arquitecto espanhol Antoni Gaudí (1852-1926) e muito particularmente do também espanhol Félix Candela (1910-1997)..
Abaixo estão alguns trabalhos baseados no parabolóide hiperbólico:
-Capela da cidade de Cuernavaca (México) obra do arquiteto Félix Candela.
-O Oceanográfico de Valência (Espanha), também de Félix Candela.
Referências
- Enciclopédia da matemática. Superfície governada. Recuperado de: encyclopediaofmath.org
- Llera Rubén. Parabolóide hiperbólico. Recuperado de: rubenllera.wordpress.com
- Weisstein, Eric W. "Hyperbolic Paraboloid." De MathWorld-A Wolfram Web Resource. Recuperado de: mathworld.wolfram.com
- Wikipedia. Parabolóide. Recuperado de: en.wikipedia.com
- Wikipedia. Parabolóide. Recuperado de: es.wikipedia.com
- Wikipedia. Superfície regida. Recuperado de: en.wikipedia.com


Ainda sem comentários