
Inclinação de uma fórmula de linha e equações, representação, exemplos
O inclinação de uma linha é a tangente do ângulo θ que a referida linha forma com o eixo horizontal, que por convenção é medido no sentido anti-horário. A inclinação de qualquer linha é sempre constante e por isso é uma de suas características mais essenciais..
Para calculá-lo, você precisa saber dois pontos na linha, cujas coordenadas são (x1,Y1) e (xdois,Ydois) Um segmento que pertence à linha é desenhado entre os dois pontos e, em seguida, os segmentos que representam a distância entre x são desenhados.1 e xdois, e entre e1 e edois, como na figura abaixo.
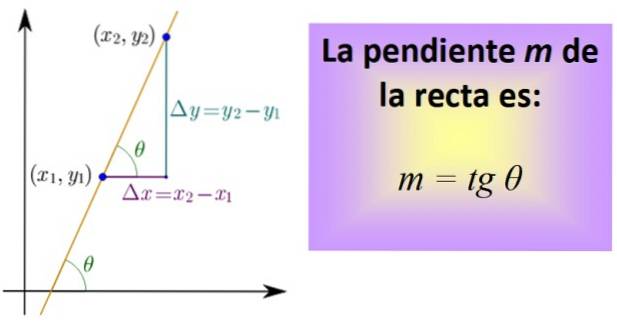
Os três segmentos formam um triângulo retângulo cujas pernas são: Δx = xdois - x1 y Δy = ydois - Y1. Eles correspondem respectivamente a um deslocamento horizontal e um deslocamento vertical..
Agora definimos um quociente, chamado de tangente do ângulo θ e abreviado tg θ, que é precisamente a inclinação m da reta:
m = tg θ = Δy / Δx
Observe que, para uma reta, esse ângulo permanece constante, independentemente dos pontos tomados para calcular sua tangente. Em qualquer caso, este valor nos dá uma medida de quão íngreme é a linha.
Através das coordenadas dos pontos selecionados, a fórmula para a inclinação é:
m = (y - y1 ) / (xdois - x1)
Índice do artigo
- 1 representação gráfica
- 2 tipos de declive
- 3 Como você calcula a inclinação de uma linha?
- 4 exercícios resolvidos
- 4.1 - Exercício 1
- 4.2 - Exercício 2
- 5 exemplos
- 5.1 Exemplo 1
- 5.2 Exemplo 2
- 6 referências
Representação gráfica
Abaixo, temos várias situações em que o conceito de inclinação é relevante. Seu valor pode ser facilmente calculado medindo o respectivo deslocamento vertical e horizontal, e então fazendo o quociente indicado no início.
Isso nos dá uma ideia do desnível ou declínio de alguma estrutura, como uma rampa, um telhado ou uma estrada:
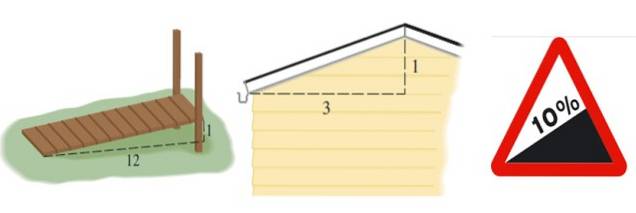
A inclinação da rampa mostrada na figura 2 à esquerda é m = 1/12, a do telhado é m = 1/3 e a da estrada é expressa em porcentagem. Uma porcentagem de 10% significa que para cada 100 metros que avançam horizontalmente, ganham-se 10 metros de altura:
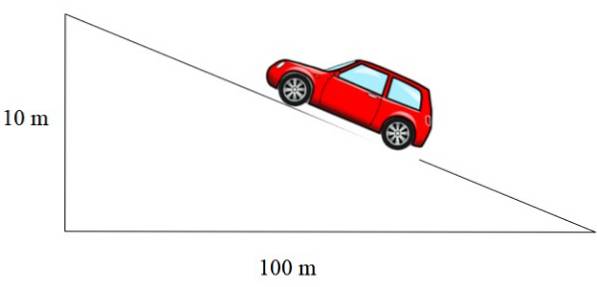
Nesse caso, a inclinação é 10/100 = 0,1, o que, expresso em porcentagem, é igual a 10%..
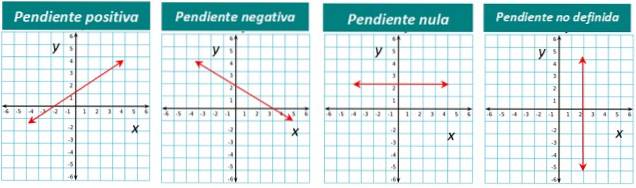
Tipos de declive
A inclinação de uma linha pode ser positiva, negativa ou zero. Por exemplo, a linha mostrada na figura 1 tem uma inclinação positiva. Agradecemos imediatamente porque vemos que a linha "sobe" se a virmos da esquerda para a direita.
Se a linha desce da esquerda para a direita, então sua inclinação é negativa. E quando uma linha é horizontal, sua inclinação é zero.
Finalmente, para linhas verticais, a inclinação não é definida.
A representação gráfica de cada tipo está abaixo:
Como você calcula a inclinação de uma linha?
Calcular a inclinação é muito simples, você só tem que encontrar o deslocamento vertical e o deslocamento horizontal, e então fazer o quociente entre ambos.
Quando temos o desenho da linha no plano cartesiano, esses deslocamentos são encontrados escolhendo quaisquer dois pontos na linha P1 E Pdois, determinar suas coordenadas e aplicar a definição dada no início:
m = (y - y1 ) / (xdois - x1 )
Uma vez que o valor da inclinação é independente da escolha de P1 E Pdois , vamos escolher um ponto P qualquer das coordenadas (x, y) que pertença à reta, cujas coordenadas não são conhecidas, e outro ponto P1 cujas coordenadas são: (x1,Y1).
A inclinação é:
m = (y - y1) / (x - x1)
Podemos limpar o Y:
e e1 = m (x - x1)
Agora suponha que o ponto P1 é a interseção da linha com o eixo vertical, de coordenadas (0, b). Substituindo isso na equação acima:
y - b = m (x - 0) → y = mx + b
Esta expressão é conhecida como a equação da reta no formulário inclinação - interceptar, uma vez que a linha é inequivocamente determinada quando sua inclinação e sua interseção com o eixo vertical são conhecidas.
Saber apenas a inclinação não é suficiente para caracterizar uma reta no plano, uma vez que infinitas retas poderiam ter a mesma inclinação, o que significa que são paralelas, mas passam por outros pontos..
Exercícios resolvidos
- Exercício 1
Encontre a inclinação da linha mostrada na figura a seguir:
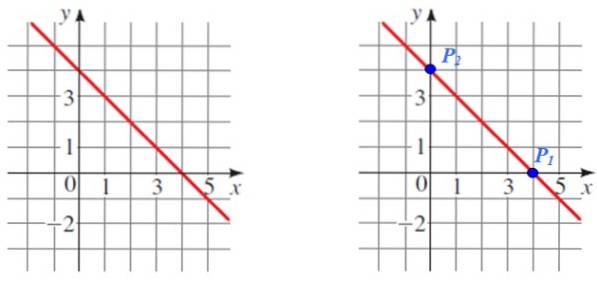
Solução
P1 E Pdois são dois pontos de fácil leitura que serão usados para o cálculo, note também que eles são as respectivas interseções com os eixos de coordenadas.
As coordenadas de cada ponto são:
P1 (4.0) e Pdois (0,4)
Substituindo a inclinação na equação:
m = (4 - 0) / (0 - 4) = 4 / (- 4) = -1
A inclinação é negativa, o que era esperado depois de olhar o gráfico.
- Exercício 2
Encontre a equação da linha que passa pelo ponto (1, -6) e é paralela à linha y = 2x - 3.
Solução
A inclinação da reta procurada deve ser a mesma de y = 2x - 3, uma vez que são paralelas. Para esta reta, a inclinação é m = 2, portanto, aquela que estamos procurando tem a forma:
e e1 = 2 (x - x1)
Agora substituímos o ponto pelo qual nossa linha passa: x1 = 1 e y1 = -6.
y - (-6) = 2 (x - 1)
Portanto, y = 2x - 2 - 6 → y = 2x - 8
Exemplos
Duas grandezas podem ser relacionadas de forma que seu gráfico seja uma linha reta. Nesse caso, diz-se que as quantidades têm dependência linear e a inclinação da linha pode ser interpretada como a taxa de variação de uma variável para a outra.
Exemplo 1
Suponha que uma piscina esteja cheia de água em um taxa constante no tempo. Naturalmente, quanto mais o tempo passa, mais água é armazenada. Bem, a taxa na qual a piscina é preenchida é precisamente a inclinação da linha que relaciona o volume ao tempo:
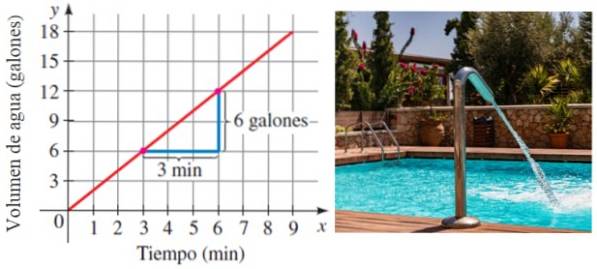
Neste exemplo, a piscina está enchendo a uma taxa de 6/3 galões por minuto ou 2 galões / minuto.
Exemplo 2
Quando um móvel se move em linha reta com velocidade constante, a inclinação do gráfico de posição em função do tempo não é outra senão a referida velocidade. O gráfico mostra um móbile com velocidade positiva, o que significa que está se afastando da origem.
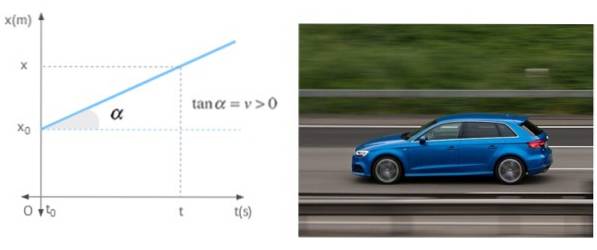
Referências
- Alvarez, J. A inclinação de uma rodovia. Recuperado de: geogebra.es.
- Carena, M. 2019. Manual de Matemática Pré-Universitária. Universidade Nacional do Litoral.
- Hoffman, J. Selection of Mathematics Topics. Volume 4.
- Jiménez, R. 2008. Algebra. Prentice Hall.
- Stewart, J. 2006. Pré-cálculo: Matemática para Cálculo. 5 ª. Edição. Cengage Learning.
- Zill, D. 1984. Algebra and Trigonometry. Colina Mcgraw.



Ainda sem comentários