
Cálculo de peso (física), unidades, exemplos, exercícios

O peso é a força com a qual a Terra atrai objetos para sua superfície. Cada vez que um objeto é derrubado, ele cai no chão, não é capaz de escalar sozinho, nem fica sem peso no meio do caminho, porque a Terra o atrai..
Todos os objetos se atraem invariavelmente, mesmo os menores, apenas a magnitude da força com que o fazem é proporcional à massa. Isso significa que objetos com pequena massa exercem pouca força sobre os outros, mas corpos celestes como a Terra são capazes de exercer uma força muito grande..
A Terra mantém a Lua orbitando ao seu redor graças a esta força atrativa, que é chamada atração gravitacional quando se trata de objetos que estão longe da superfície da terra, e peso quando os objetos estão próximos.
Disto se segue que a força da gravidade não requer que os objetos estejam necessariamente em contato uns com os outros para agir: é por isso que se diz que é uma força de ação à distância..
Os objetos continuam a ter peso, mesmo que estejam a uma certa altura acima do solo e quanto mais massivos forem, maior será o peso.
O grande cientista inglês Isaac Newton foi o primeiro a dar uma explicação sobre essa questão, por meio da lei universal da gravitação que leva seu nome e que desde então tem servido para entender como os objetos com massa interagem. Isso é muito importante, uma vez que qualquer objeto do planeta tem peso.
Índice do artigo
- 1 unidades de peso
- 1.1 O quilograma-força
- 1,2 A libra-força
- 2 Cálculo de peso e fórmula
- 3 Peso como vetor
- 4 Diferenças entre peso, massa e volume
- 5 exemplos de peso
- 6 Exercício resolvido
- 7 referências
Unidades de peso
O Sistema Internacional de unidades do SI tem como unidade de peso o Newton, nomeado após Isaac Newton. Esta é a unidade para medir forças de todos os tipos.
O newton, abreviado N, é definido como a força necessária para um objeto com massa de 1kg adquirir uma aceleração de 1m / sdois. Além do newton, existem outras unidades de força em uso comum, por exemplo, o seguinte:
O quilograma-força
O quilograma-força ou kilopond, abreviado como kg-f ou kp, embora comumente denominado kg sem mais, é a força que a Terra exerce sobre um objeto que está ao nível do mar e a 45º de latitude norte. É necessário especificar a localização, pois como dito, o campo gravitacional experimenta variações com a altura e latitude..
Quando alguém diz que pesa 45 kg, o que ele realmente quer dizer é que seu peso é de 45 kg-f, porque o quilograma é a unidade reservada para a massa.
A equivalência entre kg-f e N é: 1kg-f = 9,8 N
Pound-force
O libra-força, A abreviatura lb-f também é uma unidade de força análoga a kg-f, uma vez que é a força que a Terra exerce sobre um objeto de 1 lb de massa. E como acontece com o kg-f, não há problema com os valores quando você está na Terra, ou seja, um objeto de massa l lb, pesa 1 lb-f.
A equivalência em lb-f e N é: 1 lb-f ≡ 4,448222 N.
Cálculo de peso e fórmula
O peso de um objeto é proporcional à sua massa. Quanto maior for a massa, maior será o peso.
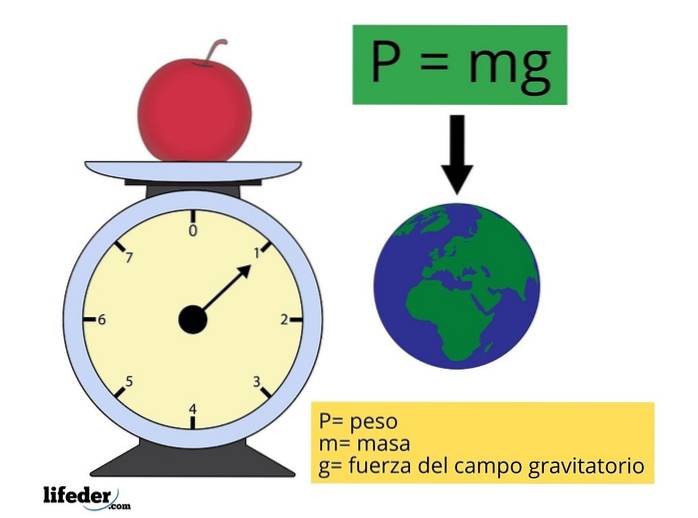
A fórmula para encontrar a magnitude do peso P (ou também W, como às vezes é denotado, por "Peso" em inglês) é muito simples:
P = mg
Onde m representa a massa do objeto e g é a magnitude da aceleração da gravidade (intensidade do campo gravitacional ou gravidade), aproximadamente constante e cujo valor é tomado como 9,81 m / sdois para os cálculos mais frequentes.
O peso é um vetor e letras em negrito são usadas para distinguir entre um vetor e sua magnitude. Desta forma, quando se fala em P entende-se que é o valor numérico e quando está escrito P referência é feita ao vetor:
P = m ∙g
O g em negrito está o campo gravitacional da Terra, ou seja, a influência que a Terra exerce sobre o espaço que a circunda, independentemente de haver ou não outro corpo que a perceba. Qualquer objeto com massa tem seu próprio campo gravitacional, seja ele pequeno ou grande.
A intensidade do campo gravitacional da Terra g não é totalmente constante. Possui pequenas variações que surgem principalmente porque a Terra não é uma esfera perfeita e também devido às diferenças locais de altura e densidade. Mas para a maioria das aplicações, o valor 9,81 m / sdois Funciona muito bem.
Outros corpos celestes têm seu próprio campo gravitacional característico, portanto, a aceleração da gravidade difere dependendo do planeta ou satélite. O mesmo objeto teria um peso diferente em cada um, logo o peso não é uma propriedade característica das coisas, mas da matéria em geral..
Peso como vetor
O peso é um vetor e, portanto, tem magnitude, direção e sentido. Nas proximidades da superfície terrestre, o peso é um vetor na direção vertical e a direção é sempre para baixo.
Normalmente, a direção vertical é nomeada como o eixo Y ou z, e a direção para baixo recebe um sinal + ou - para distingui-la da direção para cima. A escolha depende da localização da origem. Na imagem abaixo, a origem foi escolhida no ponto de queda da maçã:
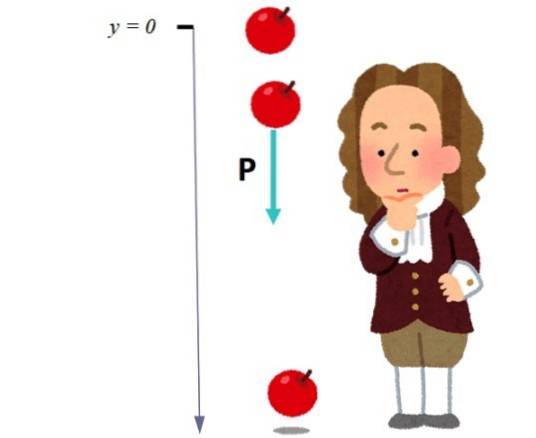
O vetor unitário j, um vetor de magnitude igual a 1, é usado para marcar e distinguir a direção vertical. Em termos deste vetor, o peso é escrito assim:
P = mg (- j)
Onde o sinal negativo é atribuído à direção descendente.
Diferenças entre peso, massa e volume

Esses três conceitos costumam ser confundidos, mas revendo as características de peso, é fácil diferenciá-lo de massa e volume..
Para começar, o peso depende do campo gravitacional onde o objeto está. Por exemplo, na Terra e na Lua a mesma coisa tem um peso diferente, embora o número de átomos que a compõe permaneça constante..
Massa é uma quantidade escalar, relacionada ao número de átomos que compõem o objeto e é evidenciada pela resistência que o objeto possui para mudar seu movimento, propriedade denominada inércia.
Por sua vez, o volume é a medida do espaço que um objeto ocupa, outra quantidade escalar. Dois objetos com o mesmo volume não têm o mesmo peso, por exemplo um cubo de ferro pesa muito mais que um cubo de poliestireno com as mesmas dimensões.
Em resumo:
- A massa está relacionada à quantidade de matéria que um corpo possui.
- Peso é a força exercida pela Terra sobre esta massa, proporcional a ela.
- Volume é o espaço ocupado pela matéria.
Deve-se notar que sendo grandezas escalares, nem a massa nem o volume têm direção ou sentido, mas apenas valor numérico e uma unidade adequada. Por outro lado, o peso, por ser um vetor, deve sempre ser expresso corretamente indicando a magnitude, a unidade, a direção e o sentido, como na seção anterior.
Exemplos de peso
Todos os objetos da Terra têm peso, você pode até "pesar" objetos que não estão na Terra, como outros planetas ou o Sol, embora por meios indiretos, é claro.
Como a faixa de pesos é muito grande, a notação científica (em potências de 10) é usada para expressar alguns que são muito grandes ou muito pequenos:
-The Sun: 1.989 × 1030 kg-f
-Júpiter: 1.898 × 1027 kg-f
-Um mosquito: 2,0 × 10-5 N
-Bebês: 34,3 N
-Uma criança: 353 N
-Pessoa adulta: 65 kg-f
-Um elefante adulto: 5,5 × 103 kg-f
-Baleia Azul: 1,0 × 106 N
Exercício resolvido
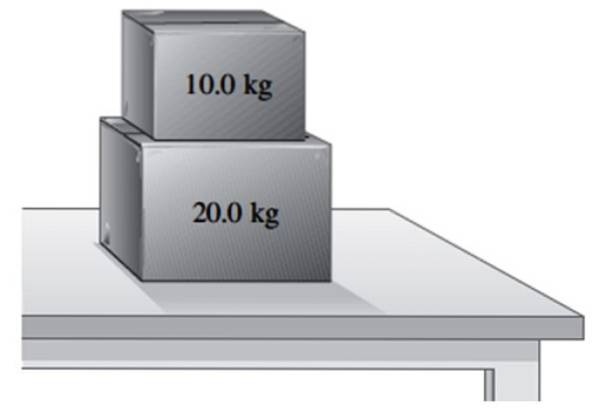
Uma caixa de massa de 20 kg repousa sobre uma mesa.
a) Encontre o peso da caixa e a força normal que a mesa exerce sobre ela.
b) Outra caixa de 10 kg é colocada em cima da primeira. Encontre a normal que a mesa exerce na caixa de 20 kg e a normal que esta exerce na caixa menor.
Solução para
É conveniente fazer um diagrama de corpo livre sobre a caixa, que consiste em desenhar as forças que atuam sobre ela..
Nessa situação, a menor caixa ainda não está no topo, portanto, existem apenas duas forças: a primeira é o peso. P que é desenhado verticalmente para baixo, como indicado nas seções anteriores e, em seguida, há o normal N, que é a força perpendicular exercida pela mesa e evita que a caixa caia.
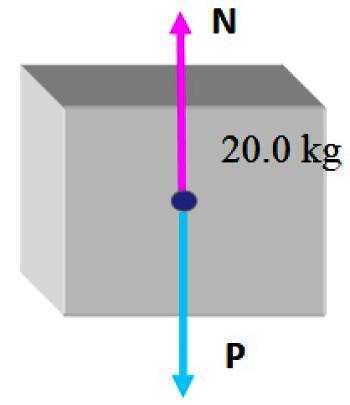
Dado que a caixa está em equilíbrio estático nessas circunstâncias, é razoável concluir que a magnitude da normal é a mesma do peso, de forma que ela pode compensar, portanto:
N = mg = 20,0 kg x 9,8 m / sdois = 196 N; dirigido verticalmente para cima.
Por sua vez, o peso é P = 196 N direcionado verticalmente para baixo.
Solução b
Agora, novos diagramas de corpo livre são feitos em ambos os objetos. Para a caixa grande as coisas mudam um pouco, já que a caixa pequena exerce força sobre ela.
As forças são as seguintes: N Y P são respectivamente o normal exercido pela mesa e o peso na caixa de 20,0 kg, que não se alterou. E a nova força exercida pela pequena caixa é N1, o normal devido ao contato com a face superior da caixa grande.
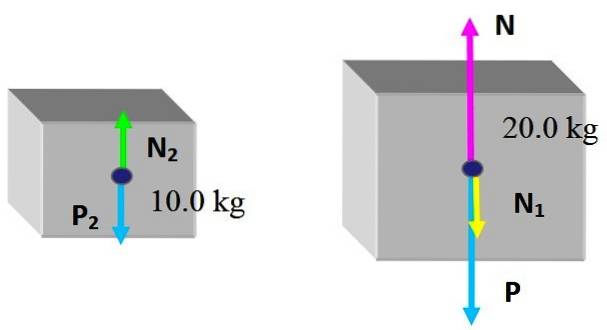
Já para a caixinha, ela recebe o normal Ndois, exercido pela face superior da caixa grande e, claro, seu peso Pdois. Uma vez que as caixas estão em equilíbrio estático:
Ndois - Pdois = 0
N - N1 - P = 0
Da primeira equação, temos que Ndois = Pdois = 10 kg x 9,8 m / sdois = 98 N. Por lei de ação e reação, a magnitude da força que a caixa pequena recebe é a mesma que ela exerce sobre a caixa grande, então:
Ndois = N1 = 98 N
A partir da segunda equação, o N normal exercido pela mesa na caixa grande é apagado, que por sua vez tem a caixa pequena no topo:
N = N1 + P = 98 N + 196 N = 294 N
Referências
- Figueroa, D. 2005. Série: Física para Ciências e Engenharia. Volume 2. Dynamics. Editado por Douglas Figueroa (USB).
- Giambattista, A. 2010. Física. 2ª Ed. McGraw Hill.
- Giancoli, D. 2006. Física: Princípios com Aplicações. 6º. Ed Prentice Hall.
- Sears, Zemansky. 2016. Física Universitária com Física Moderna. 14º. Ed. Volume 1. Pearson.
- Serway, R., Jewett, J. 2008. Physics for Science and Engineering. Volume 1. 7º. Ed. Cengage Learning.
- Thomas Griffith, W. 2007. Conceptual Physics. Mc Graw Hill.



Ainda sem comentários