
Explicação da pressão manométrica, fórmulas, equações, exemplos
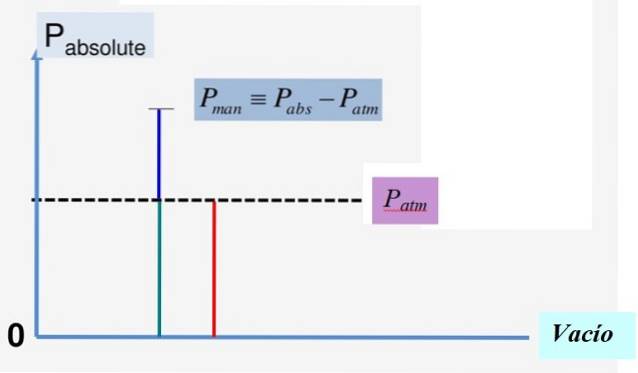
O pressão manométrica Pm é aquela medida em relação a uma pressão de referência, que na maioria dos casos é escolhida como a pressão atmosférica Patm ao nível do mar. Então é um pressão relativa, outro termo pelo qual também é conhecido.
A outra maneira pela qual a pressão é normalmente medida é comparando-a com o vácuo absoluto, cuja pressão é sempre zero. Nesse caso, falamos do pressão absoluta, que iremos denotar como Ppara.
A relação matemática entre essas três quantidades é:
Ppara = Patm + Pm
Portanto:
Pm = Ppara - Patm
A Figura 1 ilustra convenientemente essa relação. Como a pressão de vácuo é 0, a pressão absoluta é sempre positiva e o mesmo ocorre com a pressão atmosférica Patm.
A pressão manométrica é freqüentemente usada para denotar pressões acima da pressão atmosférica, como a encontrada em pneus ou no fundo do mar ou em uma piscina, que é exercida pelo peso da coluna d'água. Nestes casos, Pm > 0, pois Ppara > Patm.
No entanto, existem pressões absolutas abaixo de Patm. Nestes casos, Pm < 0 y recibe el nombre de Pressão a partir de vazio e não deve ser confundido com pressão de vácuo já descrito, que é a ausência de partículas capazes de exercer pressão.
Índice do artigo
- 1 Fórmulas e equações
- 1.1 Variação de pressão com a profundidade
- 2 exemplos
- 2.1 Princípio de Pascal
- 2.2 Paradoxo hidrostático de Stevin
- 3 exercícios
- 3.1 Exercício 1
- 3.2 Exercício 2
- 4 referências
Fórmulas e equações
A pressão em um fluido -líquido ou gás- é uma das variáveis mais significativas em seu estudo. Em um fluido estacionário, a pressão é a mesma em todos os pontos na mesma profundidade, independentemente da orientação, enquanto o movimento dos fluidos nos tubos é causado por mudanças na pressão..
A pressão média é definida como o quociente entre a força perpendicular a uma superfície F⊥ e a área da referida superfície A, que é expressa matematicamente da seguinte forma:
P = F⊥ /PARA
A pressão é uma quantidade escalar, cujas dimensões são a força por unidade de área. As unidades de sua medida no Sistema Internacional de Unidades (SI) são newton / mdois, chamado Pascal e abreviado como Pa, em homenagem a Blaise Pascal (1623-1662).
Múltiplos como quilo (103) Y mega (106) são frequentemente usados, uma vez que a pressão atmosférica está geralmente na faixa de 90.000 - 102.000 Pa, que é igual a: 90 - 102 kPa. Pressões da ordem de megapascais não são incomuns, por isso é importante se familiarizar com os prefixos.
Em unidades anglo-saxônicas, a pressão é medida em libras / pédois, no entanto, geralmente é feito em libras / polegadadois ou psi (libras-força por polegada quadrada).
Variação de pressão com a profundidade
Quanto mais nos imergimos na água de uma piscina ou no mar, mais pressão sentimos. Pelo contrário, conforme a altura aumenta, a pressão atmosférica diminui.
A pressão atmosférica média ao nível do mar é estabelecida em 101.300 Pa ou 101,3 kPa, enquanto na Fossa das Marianas, no Pacífico Ocidental - a profundidade mais profunda conhecida - é cerca de 1000 vezes maior e no topo do Everest é de apenas 34 kPa.
É claro que pressão e profundidade (ou altura) estão relacionadas. Para descobrir no caso de um fluido em repouso (equilíbrio estático), considera-se uma porção de fluido em forma de disco, confinada em um recipiente (ver figura 2). O disco tem seção transversal PARA, peso dW e altura tingir.
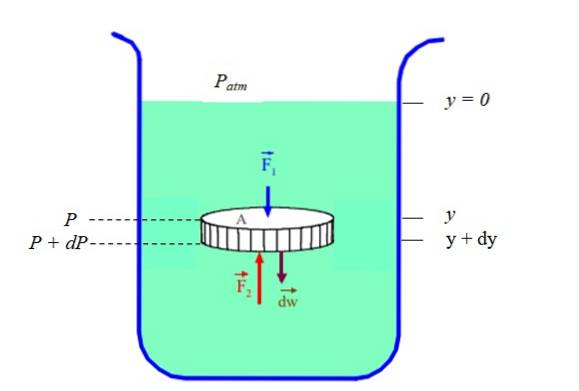
Vamos ligar P à pressão que existe em profundidade "Y"Y P + dP à pressão que existe em profundidade (y + dy) Uma vez que a densidade ρ do fluido é a razão de sua massa dm e seu volume dV, se tem que:
ρ = dm / dV ⇒ dm = ρ.dV
Portanto, o peso dW do elemento é:
dW = g. dm = ρ.g.dV
E agora a segunda lei de Newton se aplica:
Σ FY = Fdois - F1 - dW = 0
(P + dP) .A - P.A - ρ.g.dV = 0
(P + dP) .A - P.A - ρ.g. A. dy = 0
dP = ρ.g.dy
Solução da equação diferencial
Integrando os dois lados e considerando que a densidade ρ, bem como a gravidade g são constantes, a expressão pesquisada é encontrada:
Pdois - P1 = ΔP = ρ.g. (edois - Y1)
ΔP = ρ.g. ΔY
Se na expressão anterior você escolher P1 como pressão atmosférica e Y1 como a superfície do líquido, então Ydois está localizado em uma profundidade h Y ΔP = Pdois - Patm é a pressão manométrica em função da profundidade:
Pm = ρ.g.h
Caso seja necessário o valor da pressão absoluta, basta adicionar a pressão atmosférica ao resultado anterior.
Exemplos
Para medir a pressão manométrica, um dispositivo chamado Medidor de pressão, que geralmente oferecem diferenças de pressão. No final, o princípio de funcionamento de um manômetro de tubo em U será descrito, mas agora vamos dar uma olhada em alguns exemplos importantes e consequências da equação deduzida anteriormente.
Princípio de Pascal
A equação ΔP = ρ.g. (edois - Y1) pode ser escrito como P = Po + ρ.g.h, Onde P é a pressão na profundidade h, enquanto que Pou é a pressão na superfície do fluido, geralmente Patm.
Obviamente, toda vez que aumenta Po, aumenta P na mesma quantidade, desde que seja um fluido de densidade constante. É precisamente o que foi suposto ao considerar ρ constante e coloque-a fora da integral resolvida na seção anterior.
O princípio de Pascal afirma que qualquer aumento na pressão de um fluido confinado em equilíbrio é transmitido sem qualquer variação a todos os pontos do referido fluido. Através desta propriedade, é possível multiplicar a força F1 aplicado ao pequeno êmbolo à esquerda, e obter Fdois à direita.
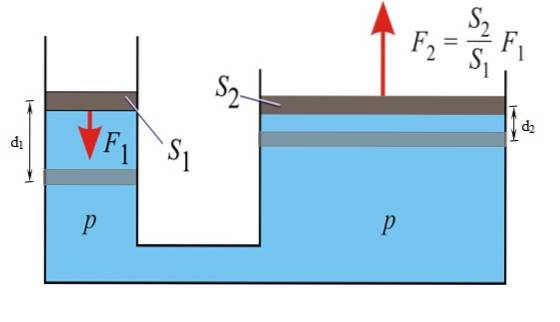
Os freios do carro funcionam segundo este princípio: uma força relativamente pequena é aplicada no pedal, que se torna uma força maior no cilindro do freio em cada roda, graças ao fluido usado no sistema..
Paradoxo hidrostático de Stevin
O paradoxo hidrostático afirma que a força devida à pressão de um fluido no fundo de um recipiente pode ser igual, maior ou menor que o peso do próprio fluido. Mas quando você coloca o recipiente no topo da balança, ele normalmente registra o peso do fluido (mais o do recipiente, é claro). Como explicar este paradoxo?
Partimos do fato de que a pressão no fundo do recipiente depende exclusivamente da profundidade e é independente da forma, como foi deduzido na seção anterior..
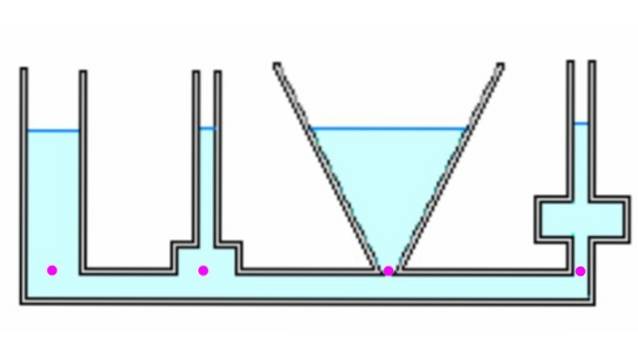
Vejamos alguns contêineres diferentes. Sendo comunicados, quando se enchem de líquido atingem todos a mesma altura h. Os destaques estão na mesma pressão, pois estão na mesma profundidade. No entanto, a força devido à pressão em cada ponto pode diferir do peso, (ver exemplo 1 abaixo).
Treinamento
Exercício 1
Compare a força exercida pela pressão no fundo de cada um dos recipientes com o peso do fluido e explique por que as diferenças, se houver.
Container 1
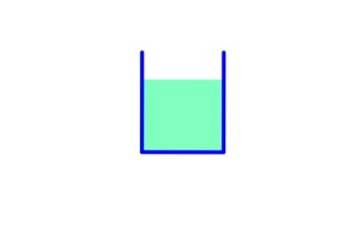
Neste contêiner a área da base é A, portanto:
Peso do fluido: mg = ρ.V.g = ρ . A .h. g
Pressão na parte inferior: ρ. g. h
Força devido à pressão: F = P.A = ρ. g. h. PARA
Peso e força devido à pressão são iguais.
Container 2
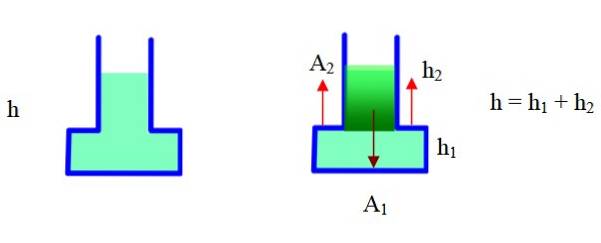
O contêiner possui uma parte estreita e uma parte larga. No diagrama à direita, ele foi dividido em duas partes e a geometria será usada para encontrar o volume total. Área Adois isso é externo para o contêiner, hdois é a altura da parte estreita, h1 é a altura da parte larga (base).
O volume total é o volume da base + o volume da parte estreita. Com esses dados, temos:
Peso do fluido: m. g = ρ . g. V = ρ . g. [PARA1 .h1+ (PARA1 -PARAdois) .hdois] =
= ρ . g (A1.hadoishdois) = ρ . g. PARA1.h - ρ . g. PARA.. hdois (Foi feito uso de h = h1 +hdois)
Pressão na parte inferior: P = ρ. g. h
Força na parte inferior devido à pressão: F = P. A1 = ρ. g. h. PARA1
Comparar o peso do fluido com a força devido à pressão mostra que este é maior do que o peso.
O que acontece é que o fluido também exerce força sobre a parte do degrau no recipiente (veja as setas em vermelho na figura) que estão incluídas no cálculo acima. Essa força para cima se contrapõe às exercidas para baixo e o peso registrado pela balança é o resultado delas. De acordo com isso, a magnitude do peso é:
W = Força na parte inferior - Força na parte escalonada = ρ . g. PARA1.h - ρ . g. PARA.. hdois
Exercício 2
Um manômetro de tubo aberto é mostrado na figura. Consiste em um tubo em forma de U, no qual uma extremidade está à pressão atmosférica e a outra é conectada a S, o sistema cuja pressão deve ser medida..
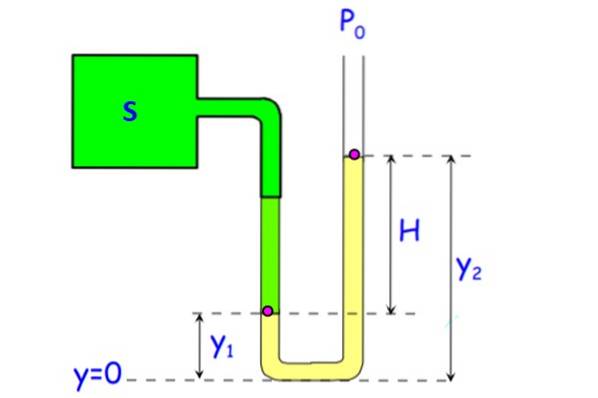
O líquido no tubo (mostrado em amarelo na figura) pode ser água, embora o mercúrio seja usado preferencialmente para reduzir o tamanho do dispositivo. (Uma diferença de 1 atmosfera ou 101,3 kPa requer uma coluna de água de 10,3 metros, nada portátil).
Ele pede para encontrar a pressão manométrica Pm no sistema S, em função da altura H da coluna de líquido.
Solução
A pressão no fundo para ambas as ramificações do tubo é a mesma, pois estão na mesma profundidade. Deixe PPARA a pressão no ponto A, localizado em y1 E PB aqueles do ponto B que está na altura edois. Uma vez que o ponto B está na interface de líquido e ar, a pressão lá é Pou. Neste ramo do manômetro, a pressão na parte inferior é:
Po + ρ.g.ydois
Por sua vez, a pressão na parte inferior para o ramo da esquerda é:
P + ρ.g.y1
Onde P é a pressão absoluta do sistema e ρ é a densidade do fluido. Equalizando ambas as pressões:
Po + ρ.g.ydois = P + ρ.g.y1
Limpando P:
P = Po + ρ.g.ydois - ρ.g.y1 = Po + ρ.g (edois - Y1) = Po + ρ.g. H
Portanto, a pressão manométrica Pm É dado por P - Pou = ρ.g. H e para ter seu valor, basta medir a altura a que o líquido manométrico sobe e multiplicar pelo valor g e a densidade do fluido.
Referências
- Cimbala, C. 2006. Mecânica dos Fluidos, Fundamentos e Aplicações. Mc. Graw Hill. 66-74.
- Figueroa, D. 2005. Série: Física para Ciências e Engenharia. Volume 4. Fluidos e termodinâmica. Editado por Douglas Figueroa (USB). 3-25.
- Mott, R. 2006. Mecânica dos fluidos. 4º. Edição. Pearson Education. 53-70.
- Shaugnessy, E. 2005. Introdução à Mecânica dos Fluidos, Oxford University Press. 51 - 60.
- Stylianos, V. 2016. Uma explicação simples do paradoxo hidrostático clássico. Recuperado de: haimgaifman.files.wordpress.com


Ainda sem comentários